机器学习

发布日期: 2021-07-31

更新日期: 2022-08-10

文章字数: 3.3k

阅读时长: 12 分

阅读次数:

基于numpy的实现代码传送门

深度神经网络（Deep Neural Networks， DNN），也称深度前馈网络（Deep Feedfoward Network，DFN）、前馈神经网络（Feedforward Neural Network，FNN）、多层感知机（multilayer perceptron，MLP），花样真多-_-||，其基础思想是感知机或者逻辑斯蒂回归

1. 输入输出

训练输入： \[ T=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中，

$x$ 为特征域，$x_i \in \mathbb{R}^{n},i =1,2,...,N$
$y$ 为标签域，$y_i \in \mathbb R^K$ ，$K$ 为输出标签集合大小，$y_i$ 是一个one-hot向量

测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^n \] 测试输出： \[ Y'=\{y'_1,\cdots,y'_{N'}\},y_i' \in \mathbb R^K \]

2. 模型效果

上图是一个由离散数据点拟合一条函数曲线的demo。

图中，红点一条关于二次函数曲线噪声点，蓝线为使用DNN拟合出关于红点的函数曲线

3. 基本定义

从DNN的各种称呼中可以看出一个关键：前馈。

这是因为数据在DNN网络的流动是单向的，更加具体的，DNN模型总体的表达式可以是对复合函数 \[ y = f(x) \] 进行套娃递归操作 \[ f(x) = h_T(x) = a_T(h_{T-1}(x)) \\ h_{T-1}(x) = a_{T-1}(h_{T-2}(x)) \\ \cdots \\ h_{2}(x) = a_2(h_{1}(x)) \] 其中，$a_i(\cdot)$ 是激活函数

上面式子中的每多嵌套一层，对应的DNN就会多加一层，如果DNN只有一层，如果激活函数是 $sign(\cdot)$ ，那么这就是一个感知机；如果激活函数是 $\text{sigmoid}(\cdot)$ ，那么这就是一个逻辑斯蒂函数。

由于以前的算力并不是很强，一般传统的机器学习只有一层，所以只是简单machine learning；后来算力提升，层数可以无限叠加，虽然也可以称其为machine learning，但是这听起来一点都不cool，于是为了体现高大上，我们就改称其为deep learning

进一步的，为了使DNN更容易理解并且看起来更cool，我们对每一层进行划分并命名，得到如下多层的DNN的结构图

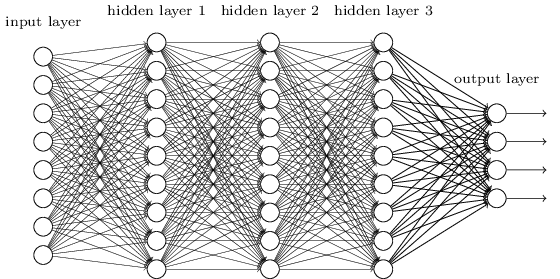
上图中，

每个圆圈称作一个神经元，代表一个特征维度，是一个一维向量，即 $h(x)$；整个竖排的圆圈组合成一个神经层 $L$，代表一个矩阵，即 $H$；每一层的神经元向量长度是一样的，是输入数据的个数 $N$。其中，只有第一个和最后一个矩阵的包含可观测的物理含义（所以这两个层不叫隐藏层，而特意称为输入层和输出层，当然，中间的隐藏层虽然没有具体的物理含义，但有时候我们会买椟还珠，弃掉输出层而取隐藏层作为输出，例如word2vec算法）。
层与层之间的连线是数据的传输过程，代表着矩阵间的运算规则。这一过程往往会引入未知变量。这个传输过程可以从两种角度进行阐述。不妨先设 $L_{t-1},L_t$ 层矩阵分别为 $H_{t-1} = [h_{t-1,ij}]_{m \times N}, H_t = [h_{t,ij}]_{n \times N}$ ，未知变量$w \in \mathbb R^n,b$
- $L_{t-1}$ 层中一个神经元的数值贡献到 $L_t$ 层中的每个神经元中，即 \[ h_{t}^{(j)} = a (w \sum_k^N h_{t-1,k}^{(j)} + b) \]
- $L_{t-1}$ 层中每个神经元的数值贡献到 $L_t$ 层中的一个神经元中，即 \[ h_{t,i} = a(\sum_k^N w_i h_{t-1,k} + b) \]
两种角度都可总结成矩阵的表示形式，为了表述方便、理解容易，一般不使用上面假设的矩阵表达形式，而改为：

假设 $L_{t-1},L_t$ 层矩阵分别为 $H_{t-1} = [h_{t-1,ji}]_{N \times m}, H_t = [h_{t,ji}]_{N \times n}$ ，未知变量 $W = \{w_i^T | 0 \leq i \leq n\} = [W_{ji}]_{m \times n},b$

于是，整个传输过程表示为 \[ h_t=a(W \cdot h_{t-1}+b) \] 或者再进一步简化为 \[ H_t = a(H_{t-1}W + b) \]

4. 模型推导

DNN的推导跟感知机或者逻辑斯蒂回归的推导如出一辙。

4.1. 前向传递

代入一些“合理”假设，对上面经典的DNN模型公式重新整理如下 \[ h_1 = \sigma(W_1\cdot x + b_1) \\ h_2 = \sigma(W_2\cdot x + b_2) \\ \cdots \\ y = h_T \sigma(W_T \cdot h + b_T) \] 其中，$\sigma(\cdot)$ 是sigmoid函数 \[ \sigma(x)=\frac{1}{1+e^{-x} } \] ## 反向迭代

反向传播就是求解个传播过程中引入的未知变量，即求解最优化问题，而DNN的最优化策略非常简单，就是常见的 “假设损失函数 -> 求损失函数对未知变量的梯度 -> 不断迭代更新参数 -> 达到收敛” 流程，其中，涉及到的最关键的数学工具是链式法则

step by step

4.1.1. 损失函数

为了推导方便，不妨采用L2 loss \[ L(y, h(x)) = \frac{1}{2} (y - h(x)) ^2 \]

注：

实际运用中，一般上不会直接使用损失函数 $L$ 进行反向传播，而会使用代价函数 $J$ \[ J(y, h(x)) = \sum_{i} L_i \] 由于 \[ \frac{\partial J}{\partial x} = \sum_i \frac{\partial L_i}{\partial x} \] 所以为了表示方便，下面使用损失函数说明反向传播的过程。

4.1.2. 优化算法

为了推导方便，不妨采用梯度下降法

但 $ h(x)$ 是一个递归函数，不能直接给出表达式，于是这里需要借助链式法则的帮助对其进行解套处理

对于第 $t-1$ 与第 $t$ 层的未知变量 $ W_t,b_t$，按照链式法则，有 \[ \frac{\partial L}{\partial W_t} = \frac{\partial L}{\partial h_T} \cdot \frac{\partial h_T}{\partial h_{T-1}} \cdots \frac{\partial h_{t+2}}{\partial h_{t+1}} \cdot \frac{\partial h_{t+1}}{\partial W_t} \] 链式展开的妙处就在于，对原本嵌套的函数，像剥洋葱一样，一层一层展开，然后对每一小段分别求解

展开后的公式链可以看成是对三部分进行求解

由于 $L = \frac{1}{2} (y - h_T) ^2$，故 \[ \frac{\partial L}{\partial h_T} = y - h_T \]
由于 $h_{t+1}=a(W_{t} \cdot h_{t}+b) = a(g(h_t))$，故 \[ \frac{\partial h_{t+1}}{\partial h_{t}} = \frac{\partial h_{t+1}}{\partial g_{t}} \cdot \frac{\partial g_{t}}{\partial h_{t}} = a'(g_t)W_t^T \] 其中，$a'(x) = a(x)(1-a(x))$
由于 $h_{t+1}=a(W_{t} \cdot h_{t}+b) = a(g(h_t))$，故 \[ \frac{\partial h_{t+1}}{\partial W_t} = \frac{\partial h_{t+1}}{\partial g_{t}} \cdot \frac{\partial g_{t}}{\partial W_{t}} = a'(g_t)h_t^T \]

然后将上面部分拼接在一起即可

变量 $b$ 的梯度计算同理 \[ \frac{\partial L}{\partial b_t} = \frac{\partial L}{\partial h_T} \cdot \frac{\partial h_T}{\partial h_{T-1}} \cdots \frac{\partial h_{t+2}}{\partial h_{t+1}} \cdot \frac{\partial h_{t+1}}{\partial b_t} \] 可以看出前两部分的计算一样，只有最后一部分略有不同 \[ \frac{\partial h_{t+1}}{\partial b_t} = a'(g_t) \] 可以看出和 $W_t$ 的梯度计算只相差了一个 $h_t$

最终，未知参数的更新过程整理如下 \[ W_t \leftarrow W_t - \eta \delta_t \cdot h_t^T \\ b_t \leftarrow b_t - \eta \delta_t \] 其中， \[ \delta_t = (y - h_T) \cdot a'(g_T)W_T \cdots a'(g_{t+1})W_{t+1} \cdot a'(g_t) \]

这是从整个数据流的角度来看反向传播的过程，如果单独把一个隐藏层拿出来，则需要求的梯度项是 $\frac{\partial h_{t+1}}{\partial h_{t}}$、$\frac{\partial h_{t+1}}{\partial W_{t}}$（如果存在未知量 $W_t$）、$\frac{\partial h_{t+1}}{\partial b_{t}}$（如果存在偏置量 $b_t$）

5. 一些总结

5.1. 优缺点

优点：

模型结构非常灵活，自由度很高，非常适合diy。DNN的推导并不复杂，甚至比很多传统的机器学习简单得多，从上面的推导流程中也可以说明这一点。其构建的本质就是一个搭积木的过程，所以非常容易上手。模型中的绝大部分结构是可以像零件一样进行更换，而且理论上，只要找到一个梯度可求的函数，就可以对网络中的结构进行更换。而这恰恰也是神经网络的一大卖点。所以，与其说DNN是一个模型，不如说这是一个框架（还有后续的seq2seq框架），其奠定后续神经网络发展的一个方向。而事实上，后序很多对DNN的改进就是基于这一原理进行的。例如，使用卷积计算代替矩阵乘法计算，便得到了CNN模型。
一些可替换“零件”的选择：
可以处理很多传统机器学习不能解决的复杂问题。例如，”你是一个好人“，这句话在不同的语境下，可以表示完全不同的意思，其非线性程度之大，是传统线性的机器学习望而却步的，但是神经网络，却可以通过不断叠加线性层，一点一点地”掰弯“这条直线。所以理论上，任意的非线性情况，都可以用神经网络进行拟合。可以认为这是一个万能的工具。

缺点：

可解析性问题。这个问题也是一直以来是神经网络备受争议的点。大多数传统的机器学习的推导是严谨的，背后有强有力的定理支撑，有对应的物理意义。而神经网络，整个模型相当于一个黑盒子，这个黑盒子可以靠逼近拟合万物，而至于这个黑盒子干了什么，nobody knows except the god，很多时候其有效性只能通过宏观的数据实验结果来说明的，所以往往会陷入 it works but I don't know why 的情况。事实上，如今大部分深度学习的研究都是从实验结果反推回一般规律。
可控性问题。正是因为其解析性差，我们很难从一个坏的预测结果中找出问题出在哪一个隐层哪一个参数上。可控性差会引来道德伦理、责任归属问题。例如，一张猫的照片，神经网络告诉你这是一只狗，那最终谁需要对这个结果负责呢？又或者在医疗行业，你是否信任一个完全由人工智能给出的结果呢？
资源消耗问题。由于参数、迭代次数多，对于一些简单的、数据量少的任务，虽说神经网络无所不能，但套用一个神经网络总是牛刀小用的，不仅训练消耗的时间、空间资源多，而且往往会因为过拟等问题，导致最终效果很差。
随着DNN模型的深度逐渐加深，还会带来两方面的问题：
- 由于每一层神经网络都只能求解出局部最优解，当层数加深，误差就会被累积，从而逐渐偏离全局最优解
- 如果激活函数存在着饱和层落入饱和层中的数据，其导数趋于0，表示该处已无法优化，即所谓的梯度消失现象。没经过一层，梯度的幅度都会有所衰减，层数逐渐加深，越来越多的数据落入饱和区，最终就会出现整体梯度消失问题；相反，如果存在求导大于1的区域，落去此区间的数据就有可能出现梯度爆炸的问题。一般来说，梯度消失情况比较常见，但梯度爆炸出现的后果比较严重，一般模型都不能收敛。