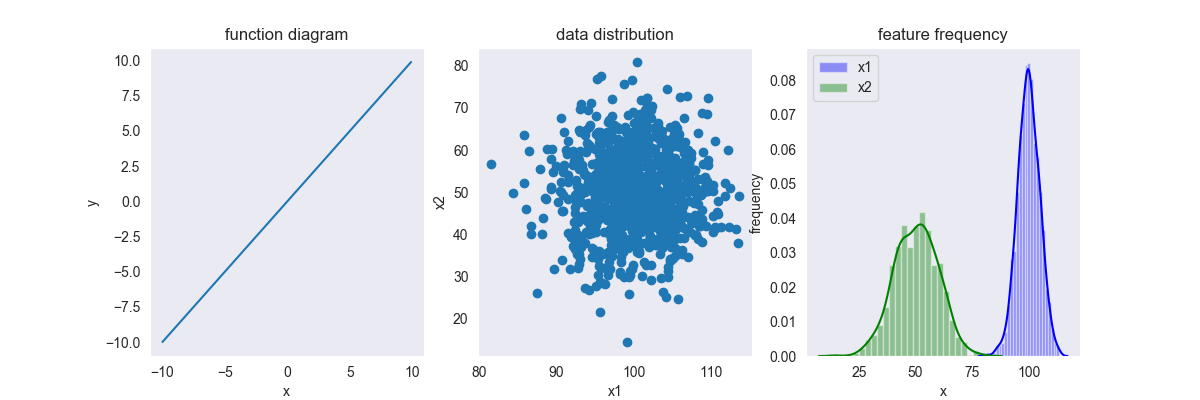
基于numpy的实现代码传送门
1. 基本定义
激活函数(Activation Function)也属于特征变换的一种,但又与上一篇中提到的特征缩放有所区别,特征缩放函数一般只对输入进行变换,激活函数一般只对输出进行变换,且一般只用于线性模型,其中以神经网络中的使用最为广泛。
激活函数一般可分为应用于回归模型和应用于分类模型的函数,对于神经网络,一般输出层是分类模型,隐藏层是回归模型,目前分类激活函数基本完善,更多的是对回归激活函数的研究与改进。
激活函数一般具有以下特点:
用于将线性模型转化为非线性模型。由于线性模型能解决的问题非常有限,所以需要将其提升至非线性的空间。一种最简单有效的方法就是变换空间坐标系。与线性核不一样的是,线性核是对每个坐标轴进行投影,而激活函数是对整个特征空间进行投影。所以很多时候,一层变换能力还是很弱,但由于线性函数的可加性和其次性,我们可以对模型进行堆叠,形成复杂的非线性问题,这个在后面提到神经网络的时候还会详细介绍。这个特点适用于各种激活函数。(上面是从充分性的角度来分析的,也可以从必要性的角度来分析。每一层神经网络的输出都需要经过非线性变换。假设激活函数是线性的,则多层神经网络和一层神经网络的效果是一样的)
将回归结果转换成分类结果。一般线性模型的输出都是回归预测结果,一件简单但不是很有效的方法是,直接添加阈值将其改成分类结果(如sign函数),但这样系统函数是一个不连续的函数,不仅为数值求解带来不便,而且由于函数不光滑,在阈值点附近的两个不同类别的预测点,这些点的差距会因此被无限放大,最终模型变得非常不稳定且不可靠。所以一般需要一个连续可导且足够光滑的函数,对其进行过渡式的“掰弯”处理。这类函数应该具有一段线性的过渡区。这个特点多适用于回归型激活函数,以二分类的sigmoid函数和多分类的softmax函数最为典型。(对于回归型激活函数来说,这个作用反而是个副作用,因为激活函数的导数表示其变量更新的幅度大小,而如果想要有一个稳定的分类结果输出,则一定需要有一段饱和区,而这段饱和区会造成梯度消失问题)
对输出值产生兴奋或抑制效果。类比生物上的神经元细胞,对于神经细胞,一般情况下为抑制态,只有输入超过一定的阈值,细胞才会变成兴奋态,对输入数据进行处理。这类函数多用于模型的中间层,以ReLU函数最为典型。
特征归一化处理。对于神经的网络的中间层,上一层的输出时下一层的输入,如果上一层的输出的取值范围很大、每个特征间的差距很大,将会影响到下一层的训练结果。对于最终的输出层,输出值范围太大,会使误差值更新过大,模型容易发散不收敛。所以这类函数应该具有一个相对明确的值域空间,可用于模型的任意层。(当然这个作用对于回归型函数来说并不是很关键,而且由于值域确定还会带来梯度消失等问题。)
综上,可以总结出激活函数一般具有如下性质:非线性、连续、便于求导、值域范围相对明确。只要符合上诉性质的函数理论上都可以作为激活函数。
2. 输出样例
下面是一个没有添加激活函数的输出样例,即 \[ y=x \] 其中, \(x \in [-\infty, +\infty],y \in [-\infty, +\infty]\) 其导数为 \[ y'=1 \]
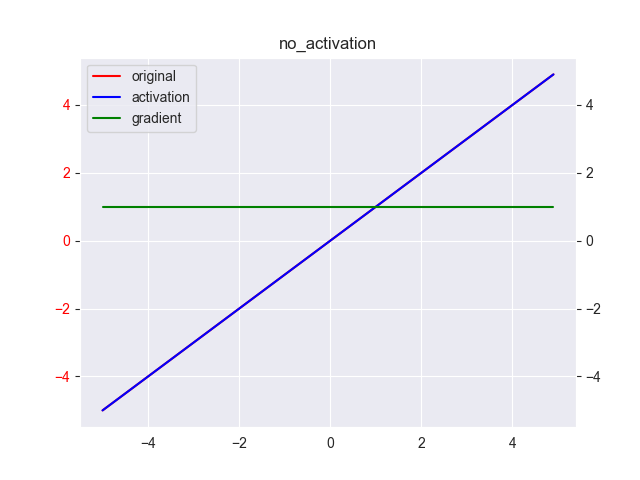
出于展示的美观,上图中采用了双坐标,红线(上图中红线被蓝线覆盖了)表示原方程 \(y=x\),对应左侧坐标系;蓝线和绿线分别表示激活函数及其导数,对应右侧坐标系。下同。
3. sigmoid
sigmoid函数又称logistics函数,以其曲线形如“S”得名。只用于二分类任务,其表达式为 \[ y = \frac{1}{1+e^{-x} } \]
其中, \(x \in [-\infty, +\infty],y \in [0,1]\) 其导数为
\[ y' = \frac{e^{-x}}{(1+e^{-x})^2} \\ = y(1-y) \]
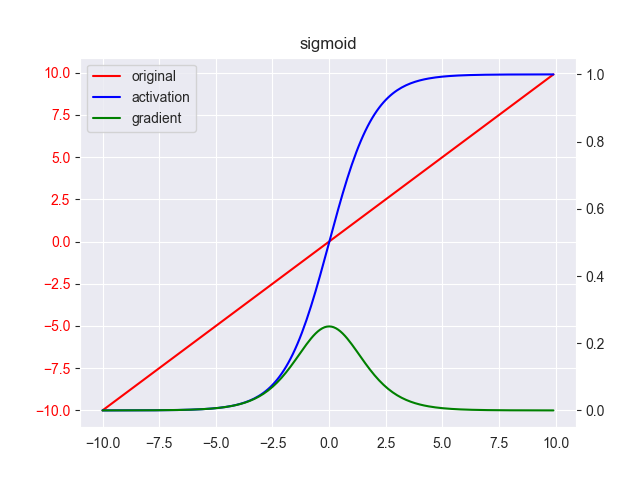
其中,\([-6,6]\) 称为线性区,其他区域称为饱和区。
这个是早期神经网络用得最多的激活函数,可以称为宗师级激活函数,其具有很多优点。
优点
- 求导表达式简单。
- 函数平滑,对应的求导表达式表达式的值域范围很窄,所以在梯度下降时,变量更新的幅度很小,不容易发散,所以训练很稳定。
缺点
- 梯度消失。正是由于sigmoid过于平滑,这也成为sigmoid函数作为中间层的激活函数时的缺点。可以看出,函数趋近于0或1的部分非常平坦,导数趋向于0,我们称这种情况为神经元饱和。饱和导致了神经元的权重无法继续更新,即梯度消失问题。(有一种看法认为(忘记该看法的出处了,后面找到再补),梯度消失是由于不好的初始化造成的,理论上存在一个完美的初始化,使数据完全不落在饱和区中)
- 不以0为中心,即函数总体期望不为0,则会出现偏移现象,容易学习到噪声。
- 计算成本高昂。对于这个问题,可以预先缓存一个sigmoid表,表中存储 \([-6,6]\) 区域内一定细粒度的计算结果,到了实际计算的时候,直接查表即可。
4. tanh
tanh函数式对不以0位中心的问题的改进,其表达式为 \[ y = \frac{e^x - e^{-x} }{e^x+ e^{-x} } \]
其中, \(x \in [-\infty, +\infty],y \in [-1,1]\) 其导数为
\[ y' = 1-y^2 \]
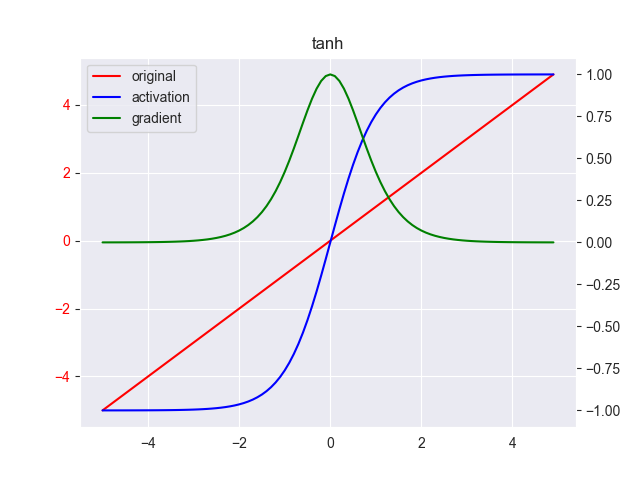
线性区为 \([-2,2]\),其他区域为饱和区
改进后,函数以0位计算中心,即函数的总体期望为0,但梯度消失问题并没有得到解决,甚至饱和区域变大了,所以梯度消失问题更加严重。
5. softmax
softmax函数一般是对二分类问题的改进,使其可用于多分类任务(可以看做是多个sigmoid函数,在二分类情况下,softmax函数就弱化成sigmoid函数),其表达式为 \[ y_i = \frac{e^{x_i} }{\sum_j e^{x_j}} \]
其中, \(x \in [-\infty, +\infty],y \in [0,1]\)
这个函数不能进行整体求导,需要分段求解。
设当前预测的样本为 \(i\) ,则对目标输出样本 \(j= \arg \max_j y_j\) 求导为
当 \(i = j\) 时 \[ \begin{array}{ll} \frac{\partial y_{i} }{\partial x_j } &= \frac{\partial}{\partial x_j } \frac{e^{x_i} }{\sum_k e^{x_k} } \\ &= \frac{(e^{x_i})' \sum_k e^{x_k} - e^{x_i} \cdot e^{x_j} }{(\sum_k e^{x_k})^2 } \\ &= y_i(1-y_i) \end{array} \] 当 \(i \neq j\) 时 \[ \begin{array}{ll} \frac{\partial y_{i} }{\partial x_j } &= \frac{\partial}{\partial x_j } \frac{e^{x_i} }{\sum_k e^{x_k} } \\ &= \frac{0 \cdot \sum_k e^{x_k} - e^{x_i} \cdot e^{x_j} }{(\sum_k e^{x_k})^2 } \\ &= -y_iy_j \end{array} \]
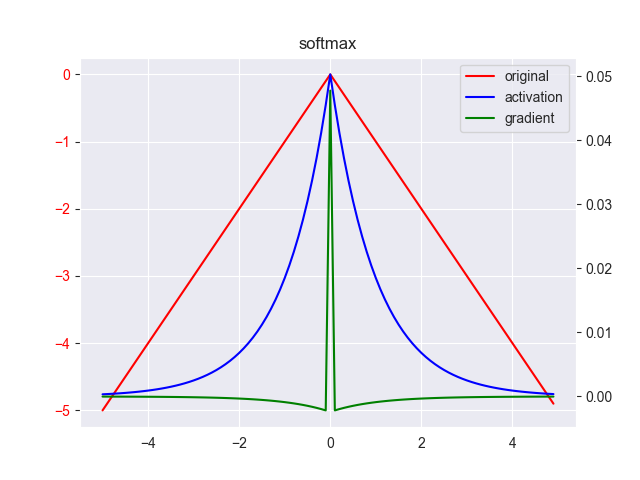
softmax的思想很简单,先对所有的类别做归一化处理,然后把其中数据值较大的类别给拉高,而且归一化后,范围较小的数据值较大的区域,占领了系统绝大部分的能量。
即可以简单描述为“马太效应”:强者愈强、弱者愈弱,两极分化。
softmax函数一般都作为最后输出层的激活函数,后面接的就是损失函数了。而softmax的损失函数的标配是交叉熵。
从最优化的角度来看(充分条件),softmax交叉熵的求导公式非常简单,使得后序的反向求导变得简单,所以softmax函数应该选择交叉熵作为损失函数;
从概率分析的角度来看(必要条件),softmax表示各标签的分布;交叉熵可以拆分为熵和相对熵(KL散度)两部分。KL散度可以衡量概率分布相似度,即预测分布越接近实际分布,KL散度越小,所以交叉熵可以作为softmax的损失函数。
一种观点认为,softmax是one-hot的soft版本,sigmoid是sign的soft版本
6. ReLU
修正线性单元(rectified linear unit,ReLU)是对梯度消失问题的改进,其表达式为
\[ y = \max(0, x) \]
其中, \(x \in [-\infty, +\infty],y \in [0,+\infty]\) ,其导数为 \[ y' = \left \{ \begin{array}{ll} 0 & ,x \leq 0 \\ 1 & ,x > 0 \end{array} \right . \]
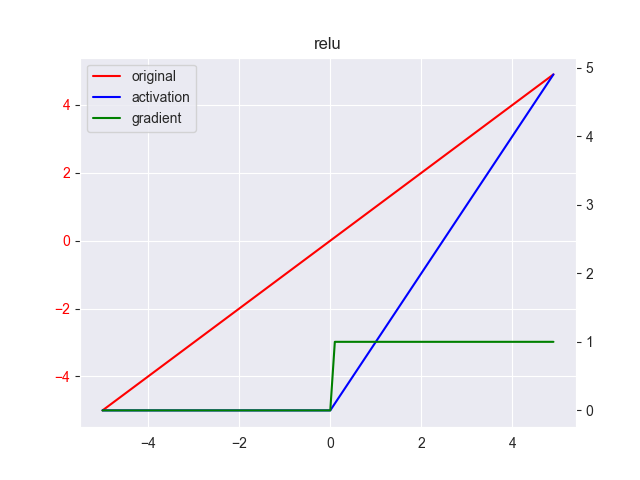
首先这个激活函数很特别,与传统的激活函数有很大的区别。我们先来看下其缺点
缺点
- 非连续性。该函数由负半区域和正半区域问题组成,在0点处有两个导数,需要进行左取值或右取值处理。
- 负半区域非常粗暴地将其值置为0,这意味着模型彻底丢弃了负值区域的信息;正半区域的导数恒为1,对梯度没有衰减,意味着模型极容易出现梯度爆炸情况。所以该函数具有一定的使用条件,由于图像处理任务不存在负值,且输出多为稀疏矩阵,天然具有抗梯度爆炸的优势,所以该函数特别适合图像处理的任务,其中以CNN网络最为典型。
- 并非真正意义上的非线性函数。由于两段函数都是线性的,所以只能组合成一个很“生硬”的非线性函数,一个并不平滑,拐角也不够大的非线性函数。
尽管缺点甚多,但瑕不掩瑜,其优点太过夺目了,以至于可以忽略掉其缺点。
优点
- 一定的对抗梯度消失的能力。由于其正半部分是不饱和的,所以这一部分并不会产生梯度消失的问题。但负半区域仍然会存在消失的问题
- 正是由于其简单粗暴的处理方式,梯度计算相当简单,计算效率极高。
- 虽然非线性能力很差,但这一点用加深神经网络来弥补,而且正因为支持层数很深的神经网络而不至于太过拟合(但这会带来梯度爆炸的问题,但这暂时不在讨论范围内,后面会提到其他的优化手段),这反而成为其一大优点。
ReLU开创了一个先河,后续更是提出很多对于回归型激活函数的改进的方案,百花齐放。
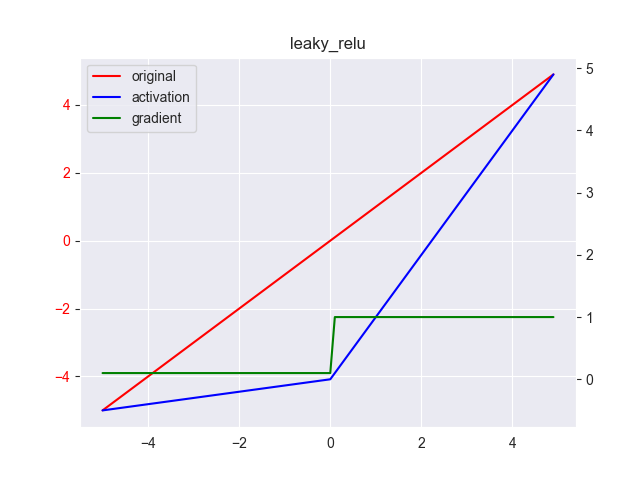
7. Leaky ReLU
Leaky ReLU是对ReLU负半区梯度消失问题的改进,其表达式为 \[
y = \max(0.1x,x)
\] 其中, \(x \in [-\infty, +\infty],y \in [-\infty,+\infty]\) ,其导数为 \[
y' = \left \{ \begin{array}{ll}
0.1 & ,x \leq 0 \\ 1 & ,x > 0
\end{array} \right .
\]
8. Parametric ReLU
这个是对Leaky ReLU继续改进,其表达式为 \[ y = \max(\alpha x,x) \] 其中, \(x \in [-\infty, +\infty],y \in [-\infty,+\infty],\alpha \in [0, 1]\) ,\(\alpha\) 为一个随机的超参数,是可学习的,其导数为 \[ y' = \left \{ \begin{array}{ll} \alpha & ,x \leq 0 \\ 1 & ,x > 0 \end{array} \right . \]
9. ELU
相关论文
指数线性单元(ELU)解决了 ReLU 的一些问题,同时也保留了一些好的方面,其表达式为 \[ y = \left \{ \begin{array}{ll} \alpha(e^x-1) & ,x \leq 0 \\ x & ,x > 0 \end{array} \right . \] 其中, \(x \in [-\infty, +\infty],y \in [?,+\infty],\alpha \in [0.1,0.3]\) ,\(\alpha\) 并非固定的取值范围,一般取0.2,其导数为 \[ y' = \left \{ \begin{array}{ll} y + \alpha & ,x \leq 0 \\ 1 & ,x > 0 \end{array} \right . \] 下面是 \(\alpha=0.2\) 的图像
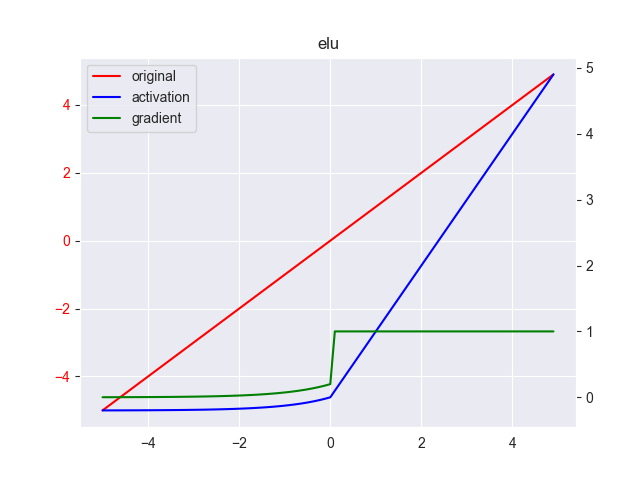
10. SELU
这个是对ELU的继续改进,其表达式为 \[ y = \lambda \left \{ \begin{array}{ll} \alpha(e^x-1) & ,x \leq 0 \\ x & ,x > 0 \end{array} \right . \] 其中, \(x \in [-\infty, +\infty],y \in [?,+\infty]\) ,按照作者论文,\(\alpha=1.67,\lambda=1.05\),并非固定的取值范围,一般取0.2,其导数为 \[ y' = \lambda \left \{ \begin{array}{ll} y + \alpha & ,x \leq 0 \\ 1 & ,x > 0 \end{array} \right . \] 下面是\(\alpha=1.67,\lambda=1.05\)的图像
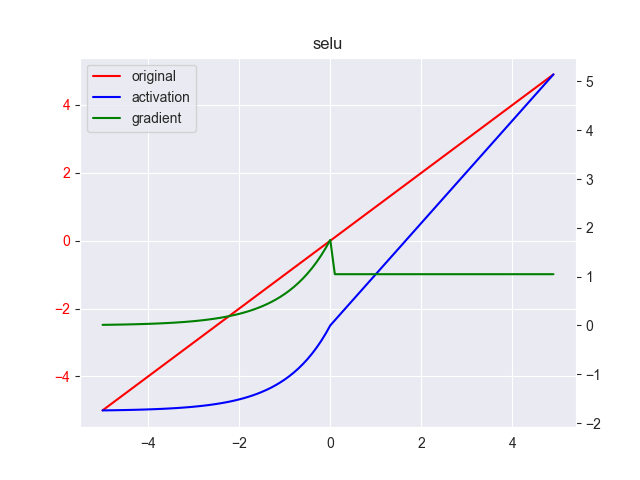
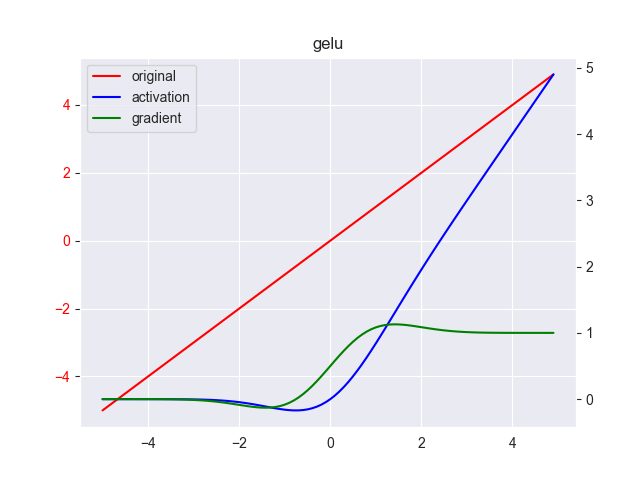
11. GELU
相关论文
高斯误差线性单元激活函数(Gaussian Error Linerar Units,GELU)是最近非常热门的激活函数,应该是目前NLP 领域的当前最佳激活函数,被广泛使用在各种大型的模型上,如:Transformer、GPT、BERT等,其表达式为 \[
y = xP(X \leq x)= x \Phi(x)
\] 其中,\(\Phi(z)\) 是高斯正态分布的累积分布,其本身服从伯努利分布(怎样理解这句话?),表达式为 \[
\Phi(z)=\frac{1}{2}\left[1+\operatorname{erf}\left(\frac{z-\mu}{\sigma \sqrt{2}}\right)\right]
\] 一般取其标准正态分布形式,原式继续简化为 \[
\Phi(z)=\frac{1}{2}\left[1+\operatorname{erf}\left(\frac{z}{\sqrt{2}}\right)\right]
\] 其中,\(erf(x)\) 为高斯误差函数(Error Function or Gauss Error Function),定义为 \[
\operatorname{erf}(x)=\frac{1}{\sqrt{\pi}} \int_{-x}^{x} e^{-t^{2}} \mathrm{d} t=\frac{2}{\sqrt{\pi}} \int_{0}^{x} e^{-t^{2}} \mathrm{d} t
\] 上式难以直接求解,其逼近计算的近似值为 \[
y = 0.5 x\left(1+\tanh \left(\sqrt{2 / \pi}\left(x+0.044715 x^{3}\right)\right)\right)
\] 或由Logistic distribution function(因为Logistic distribution和Gaussian distribution是相近的)近似拟合得到 \[
y = x \cdot sigmoid(1.702x)
\] 其中, \(x \in [-\infty, +\infty],y \in [?,+\infty]\) ,使用wolframalpha拟合出来的导数大致为 \[
y' =0.5 \tanh \left(0.0356774 x^{3}+0.797885 x\right) +\left(0.0535161 x^{3}+0.398942 x\right) \operatorname{sech}^{2}\left(0.0356774 x^{3}+0.797885 x\right)+0.5
\]
该函数的思想是根据输入的分布对其进行随机正则化处理,为其匹配一个0或1的随机值,将非线性和随机正则化进行了融合,是一种Adaptive Dropout
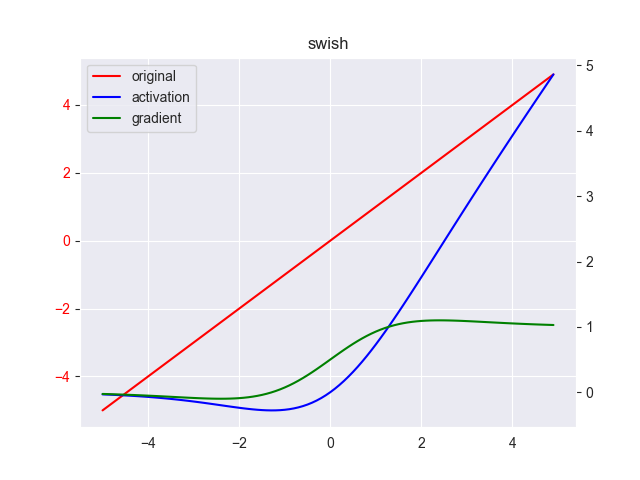
12. Swish
Swish是对ReLU函数的改进,而且有实验证明其性能优于ReLU函数,具体见Swish 激活函数的性能优于 ReLU 函数一文 \[
y = \frac{x}{1+e^{-x} }
\] 其中, \(x \in [-\infty, +\infty],y \in [?,+\infty]\) ,其导数为 \[
y'= y + \frac{1 - y}{1+e^{-x} }
\]
Swish 具备无上界有下界、平滑、非单调的特性。
可以看出这仅仅是对sigmoid函数再乘上一个x,并非什么高深的函数,这启示我们,只要有足够的想象力,并一定需要很复杂的函数,只要实验上是work的,我们也可以创造属于自己的激活函数。
13. Dropout
相关论文
最后,我们来提一个很特殊的激活函数——dropout函数,其表达式为 \[ y = x \cdot r \] 或 \[ y = \frac{x \cdot r}{p} \]
其中,\(r \sim B(p)\)
其原理非常简单粗暴,就是在每次输出的时候,按照概率p随机丢弃(即将值置为0)一部分的输出。
丢弃意味着放弃掉一部分输出的计算,而且部分置0意味着随机得到了一批新数据,dropout后的样本要么看做是总样本的局部样本,要么看做样本的噪声数据。无论哪种看法,最终的结果就是模型“学到”一些不一样的知识,用来质疑已经拟合知识,或者说使模型不敢太过自信地给任意一项参数太高的权值,因为模型不知道这个参数在下一轮训练中会不会被drop掉。
综上,该函数可以有效的提高计算效率以及抗过拟合能力。这种思想跟集成学习中学习多个部分分类器有点相似。
尽管实验证明这个方法是work的,但是这种做法并没有严谨的数学理论支撑,只有前向传播公式而没有对应的反向迭代公式。所以这个函数理论上不能被称为激活函数,只能算是一个trick。
由于其作用是防止过拟合,所以也有将其归为正则项的,但由于该函数是直接对输出函数进行包装,我还是将其归为激活函数一类。
还有值得一提的是,2019年,谷歌已为该函数申请了专利
14. references
CNN入门讲解:什么是激活函数(Activation Function)
Bye~