机器学习分类算法

机器学习

发布日期: 2020-10-27

更新日期: 2022-08-10

文章字数: 1.7k

阅读时长: 7 分

阅读次数:

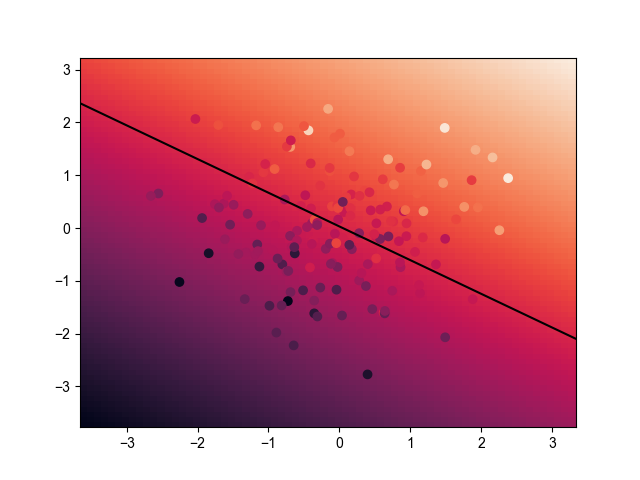
逻辑斯蒂回归（Logistic Regression，下面简称逻辑回归），是基于线性回归的分类算法

这是比较迷惑人的一点，虽然名字叫回归，但实质是分类算法。其实逻辑回归更加准确的表述应该是加入了Logistic函数的线性回归算法。原来是回归算法，加了改进函数后，就转为分类算法了，包括后面提到的softmax回归算法，也是同理。

基于numpy的实现代码传送门

1. 输入输出

训练输入： \[ T=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中，

$x$ 为特征域，$x_i \in \mathbb{R}^{n},i =1,2,...,N$
$y$ 为标签域，$y_i \in \{0,1\}$

测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^n \] 测试输出： \[ Y'=\{y'_1,\cdots,y'_{N'}\},y_i' \in \{0,1\} \]

2. 模型效果

2.1. 训练效果

2.2. 最终效果

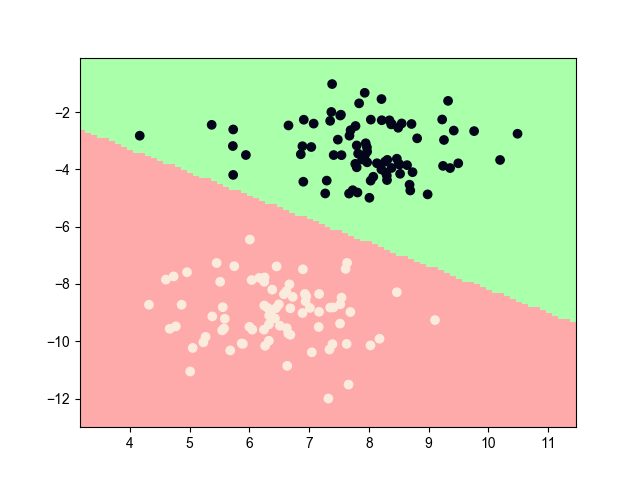
3. 模型推导

3.1. 基本方法

在线性回归中，我们假设了模型的函数为 $h(x) = wx+b$，但该值是一个预测值。于是在感知机中，通过加上一个 $sign(z)$ 函数外壳（在神经网络中，这种函数也被叫做激活函数），将连续的预测值转化为离散的分类值。感知机的做法是先对 $z$ 进行优化，再通过激活函数（这里用了神经网络的说法）对预测值进行包装。这种做法有个问题：

由于现在输入的是离散的标签，所以标签间是有很大的空隙的，预测值会有很大选择的余地，所以包装前可能是优解，但包装后的结果可能是差解了。或者换一个角度，两个细微差别的预测值在包装后差距会被强行放大，例如-0.1和0.1，就会被分为-1和1了。这显然不太合理。

逻辑回归换了种思路：直接对加了激活函数后的整体进行优化。但 $sign$ 函数是不可微的，所以这里使用了Logistic函数进行包装（由于函数图像呈S型，所以也被叫Sigmoid函数），其函数表达式和导数如下： \[ S(z) = \frac{1}{1+e^{-z}} \\ S'(z) = \frac{e^{-z}}{(1+e^{-z})^2} = S(z)(1-S(z)) \] 其函数图像如下

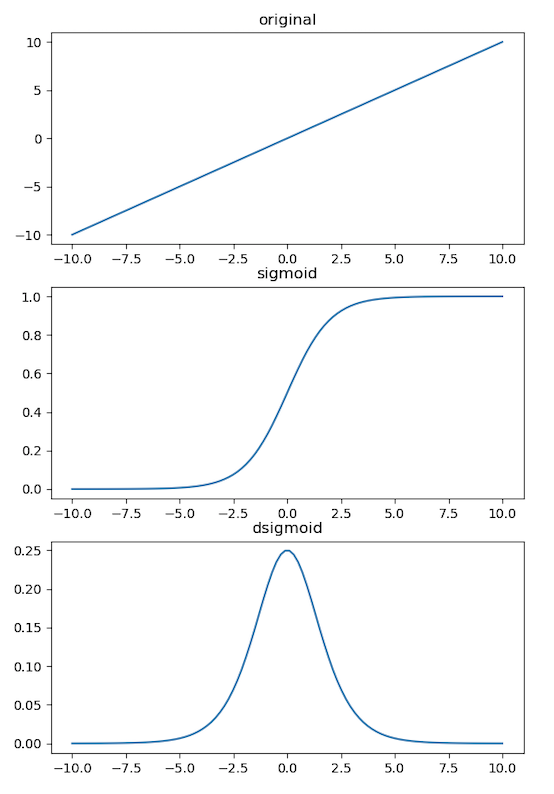
令 $wx+b=-z$，对于sigmoid函数的输出值，有如下两种构建模型函数方式

3.1.1. 基于判定边界

将函数输出看做是分类的预测值，一般设置阈值为0.5，大于阈值的数据归为1类，反之，归为0类，故模型函数表达式为 \[ f(x) = \left \{\begin{array}{ll} 1,S(x) \geq 0.5 \\ 0,S(x) < 0.5 \end{array} \right . , S(x) = \frac{1}{1+\exp(wx+b)} \]

3.1.2. 基于概率

将其看做一个后验概率值，一般上假设其为0类标签的后验概率分布，则模型的条件分布函数 \[ P(Y=1|x) = \frac{\exp(wx+b)}{1+\exp(wx+b)} \\ P(Y=0|x) = \frac{1}{1+\exp(wx+b)} \] 故模型函数表达式为 \[ f(x) = \arg \max _{c_k} \{P,1- P\},P = P(Y=0|x) \]

设事件发生是1类，则一般采用1类数据的分布作为后验概率。下面尝试从逻辑回归模型的特点进行推导。

对于二分类问题，如果一个事件发生的概率是 $p$ ，那个该事件的几率（odds，事件发生与不发生的概率）为 $p/(1-p)$，该事件的对数几率或logit函数为 \[ \text{logit(p)} = \ln \frac{p}{1-p} = \ln \frac{P(Y=1|x) }{1-P(Y=1|x) } = wx + b \] 也就是说输出 $Y=1$ 的对数几率是输入 $x$ 的线性函数表示的模型。即模型输出值与函数输出值呈正相关的关系。

当然你也可以用事件不发生的概率来推上面的结论，但一般都不使用事件不发生概率这种说法来进行推论

3.2. 学习策略

同样的，可以从两种角度出发来求得模型的优化函数

3.2.1. 基于损失函数

采用交叉熵（Cross Entropy）求其损失函数，对于二分类问题，交叉熵的表达式如下 \[ J(w,b) = - \frac{1}{N} \sum_{i=1}^N (y_i \ln p_i + (1-y_i) \ln (1-p_i)) \] 其中，$p_i$ 为事件成功的概率，即 $p_i= P(Y=1|x)$

要使模型的代价最小，应采用梯度下降法进行优化

3.2.2. 基于似然函数

模型的似然函数为 \[ l(w,b) = \prod_{i=1}^N p^{y_i} (1-p^{1-y_i}) \] 其中，$p_i$ 为事件成功的概率

为了避免向下溢出，采用对数似然函数 \[ L(w,b) = \ln l(w,b) = \sum_{i=1}^N (y_i \ln p_i + (1-y_i) \ln (1-p_i)) \] 要使模型的似然函数最大，应采用梯度上升法进行优化

3.3. 学习算法

上面学习策略无论选择哪种，殊途同归，两种方法最终的求解过程是一样的。这里采用优化损失函数的方式。

为了描述方便，令 $W=[b,w_1,w_2,...,w_n]_{1 \times n}^T,X=[1,x^{(1)},x^{(2)},...,x^{(n)}]_{N\times n}$，使得 $ X W=w x + b$，则

\[ \frac{\partial J}{\partial W} = \frac{1}{N}(X^T \cdot \frac{ \exp (XW)}{1+\exp(XW)} - X^T \cdot y) \]

更新参数 \[ W \leftarrow W - \alpha \frac{\partial J}{\partial W} \]

4. 多项逻辑回归

将二分类的逻辑回归推广至多分类的多项逻辑回归

设输入 $y_i \in \{c_1,c_2,...,c_K\}$ ，下面不加推导地给出模型函数、损失函数以及更新公式

为了描述方便，设 $w_jx_i+b=-z_{ij}$

设 $c_K$ 为正类，各个标签的值的条件概率 \[ P(Y=k|x) = \frac{\exp(z_{ik})}{1+\sum_{j=1}^{K-1} \exp(z_{ij})},k=1,2,...,K-1 \\ P(Y=K|x) = \frac{1}{1+\sum_{j=1}^{K-1} \exp(z_{ij})} \] 综合两式，可得模型函数 \[ f(x) = \arg \min \left [ P(Y=k|x) = \frac{\exp(z_k)}{\sum_{j=1}^{K} \exp(z_j)} \right ] ,k=1,2,...,K \] > 上述模型又被称为softmax回归，是线性回归分类模型的一般形式，Logistic回归是softmax回归K=2时的特殊形式 >

采用梯度下降法求解

损失函数 \[ L(W) = - \frac{1}{N}\sum_{i=1}^N \sum_{j=1}^{K}I(y_i=j)\ln \frac{\exp(z_{ij})}{\sum_{k=1}^{K} \exp(z_{ik})} \] 梯度更新表达式 \[ \frac{\partial L}{\partial W} = -\frac{1}{N} \sum_{i=1}^N(x_i I(y_i=j) - p(y_i=j|x)) \]