1. 输入输出

训练输入： \[ T=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中，

$x$ 为特征域，$x_i \in \mathbb{R}^{m \times n \times k},i =1,2,...,N$，表示一个 $k$ 通道的 $m * n$ 的图片
$y$ 为标签域，$y_i \in \mathbb R^K$ ，$K$ 为输出标签集合大小，$y_i$ 是一个one-hot向量

测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^{m \times n \times k} \] 测试输出： \[ Y'=\{y'_1,\cdots,y'_{N'}\},y_i' \in \mathbb R^K \]

2. 模型效果

上图为使用CNN做的一个手写数字识别的demo，从上往下，最上面一列数字是真实标签，第一列图像为原始图像，下面8列图像为一个8核卷积层每个通道的输出图像，最下面面一列数字为模型的预测标签。

可以看到中间的卷积层每个卷积核都可以提取出图像的部分轮廓信息的。

3. 基本定义

前面介绍的DNN模型，能用于各种拟合任务，那能不能将DNN应用与图像分类的任务中呢？可以，但传统DNN的输入 $x$ 通常是一个维度较小的向量，只需要几层少量参数即可拟合成功，而图像任务中，输入往往是 $k$ 通道 $m \times n$ 的像素矩阵，例如一个 $1000 \times 1000$ 的图像，光输入层就需要1M个节点，可想而知，后面还需要拟合参数的数量是有多庞大。

先不说这么庞大的参数量的计算资源消耗成本，传统DNN模型参数膨胀容易产生过拟和梯度爆炸问题。所以我们需要一个数学工具预先对图像输入进行信息抽取。这时候，人们想到了往神经网络中引入卷积计算。

卷积计算最开始用于信号领域的频率的过滤，后来应用于图像处理，也用来过滤图像的高低频。而图像中也存在高低频分量（高频量一般为线条轮廓和噪声点，低频量一般为颜色填充物）。

所以CNN模型的核心思想是，使用一个卷积核来抽取图像中包含大部分信息的频段，即可将一个稠密像素矩阵简化成一个稀疏矩阵，然后进行降维训练，即可减少训练的参数量。

另外，对于卷积，Hinton大佬认为，所有的神经网络的每一层都是卷积的结果。

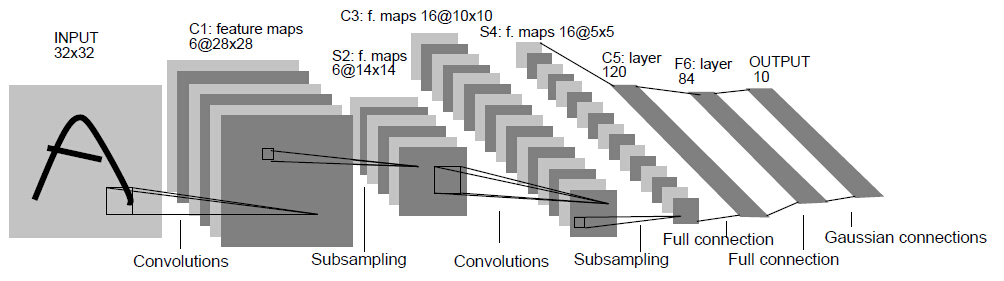
一个经典的CNN模型由输入层、卷积层（Convolutional Layer）、池化层（Pooling Layer）或下/子采样层（Down/Sub sampling Layer）、Flatten层、全连接层（Full Collection Layer）或稠密层（Dense Layer）构成

3.1. 输入层

一个图像在计算机中一般以一个 $k$ 通道的 $m n $ 像素矩阵形式进行存储，即一个图像表示为一个$m \times n \times k$ （width, height, depth）的数组，其中 $k$ 一般为1（黑白色系）或3（RGB色系）。

输入层输出维度：$[m \times n \times k]$

3.2. 卷积层

CNN模型的核心就是卷积层。

3.2.1. 卷积计算

首先来介绍卷积计算。下面直接给出其定义。

一维连续型输入卷积定义为 \[ (f * g)(t)=\int_{-\infty}^{\infty} f(\tau) g(t-\tau) d \tau \] 一维离散型输入卷积定义为 \[ (f * g)(n)=\sum_{\tau=-\infty}^{\infty} f(\tau) g(n-\tau) \] 其中，

对于$f(x)$， $x \in (x_1,x_2)$；
对于$g(x)$， $x \in (x'_1, x'_2)$；
对于 $(f * g)(x)$ ， $x \in \left (\max \{x_1,t-x'_2\}, \min\{x_2,t-x'_1\} \right )$

在信号系统中，$f(x)$ 又被称为输入响应，$g(x)$ 又被称为系统响应

以离散信号输入作为例子，推导其计算过程：

假设，$f(n)= n ,0\leq n \leq 5$ 是线性函数，$g(n) = 1, n\in R$ 是阶跃函数，求 $(f * g)(10) $

按照数学定义计算： $(f * g)(10) = f(0)g(10) + f(1)g(9) + \cdots + f(5)g(5)=15$
按照物理含义计算：将 $g(\tau)$ 以为原点中心点做对称得到 $g(-\tau)$，然后将其向左平移10个单位得到 $g(10-\tau)$，求 $f(\tau)$ 和 $g(10-\tau)$ 重合区间的内积即可，即 $[0,1,2,3,4,5] \cdot [1,1,1,1,1,1]^T=15$

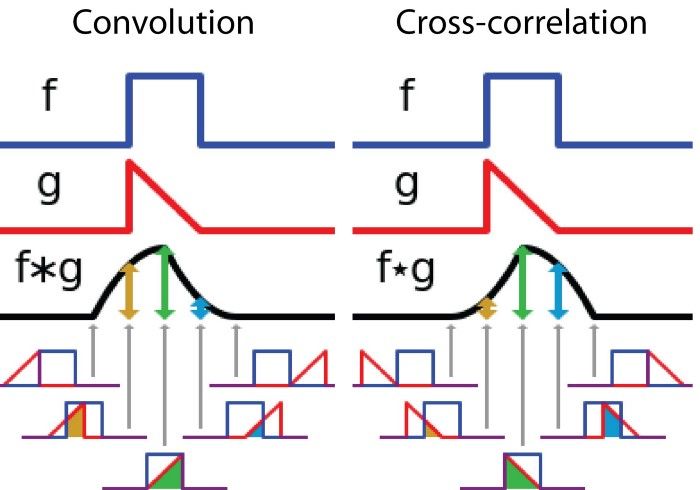
上计算过程反映了：对 $g(\tau)$ 的翻转及滑动平移，谓之“卷”；对 $f(\tau)$ 和 $g(n-\tau)$ 做相乘求和，谓之“积”。当前时刻的卷积值是之前所有时刻的输入响应的加权和，而其中的权值分布即为系统响应，故系统响应也被称作滤波器（filter）。

卷积的本质就是加权叠加，那么 $g(\tau)$ 有必要进行翻转吗？下面给出 $g(\tau)$ 翻转与不翻转的计算结果

从上图中可以看出，翻转和不翻转的卷积值是互相关的，两者是可以相互转化的，所以翻转其实不是必须。但是如果不翻转，$g(\tau)$ 是向负轴方向滑动，在信号系统中，$g(\tau)$ 是有实际的物理意义的，其只能往时序方向（即正轴方向）滑动。为了使其能正确应用于实际生活，人们就约定俗成地将$g(\tau)$ 进行了翻转。而图像处理中，filters并没有物理意义，所以图像处理中的卷积中的filters是可以不经过反转的。

来到图像处理任务。由于图像是二维输入，所以需要将一维的卷积扩展至二维。

二维离散型输入卷积定义为 \[ (f * g)(u, v)=\sum_{i} \sum_{j} f(i, j) g(u-i, v-j)=\sum_{i} \sum_{j} a_{i, j} b_{u-i, v-j} \]

与一维卷积计算差不多，二维卷积计算可以简单概括为先将 $g(u,v)$ 以原点做中心对称得到 $g(-u,-v)$（这一步可省略），然后再向左平移 $i$ 个单位、向上平移 $j$ 个单位得到 $g(i-u,j-v)$，最后重合位置做内积计算。

与一维卷积有所不一样的是：一维卷积中，滤波器一般以信号作为输入，是一个沿正方向无限延伸的物理量；而二维卷积中，滤波器没有特定具体的物理含义，一般是一个 $k_c$ 通道的 $c \times c$ 矩阵（$c$ 一般小于 $\min\{m, n\}$）。其中，一个单通道矩阵称为卷积核（kernel），$c$ 一般取3、5、7等奇数。

故二维卷积计算过程可以简单描述为，我们只需将卷积核映射到像素矩阵上，然后对重叠部分（又称为感受野（Receptive field，RF））进行加权求和，即可得到当前点卷积值。对卷积核进行滑动，即可得到所有点的卷积值。

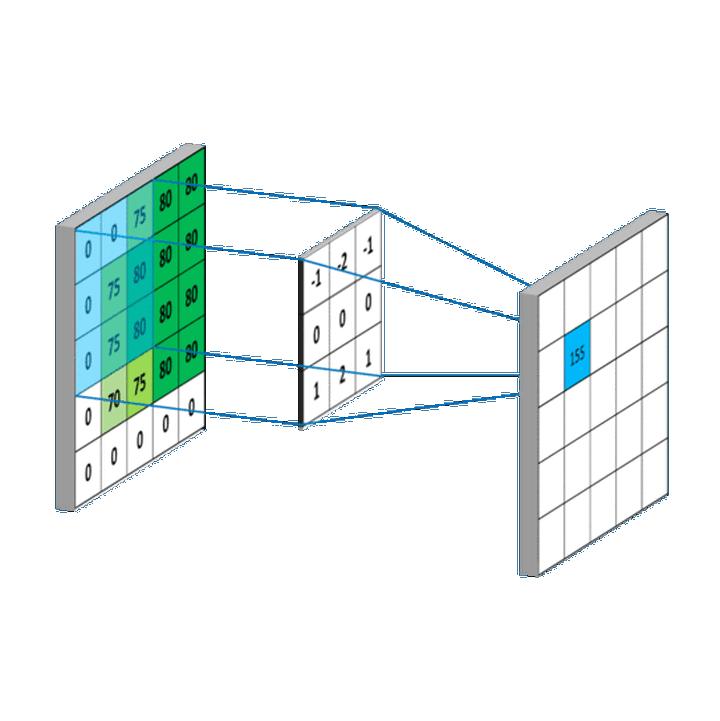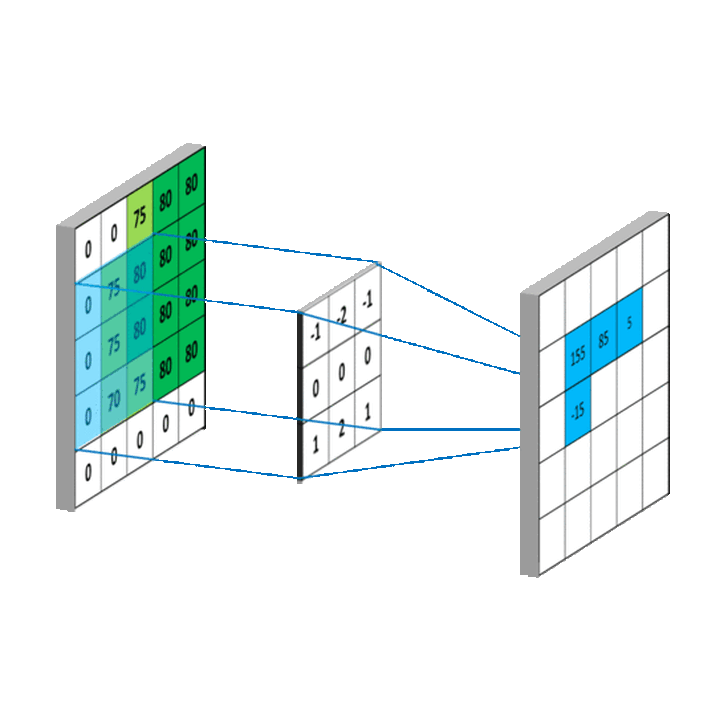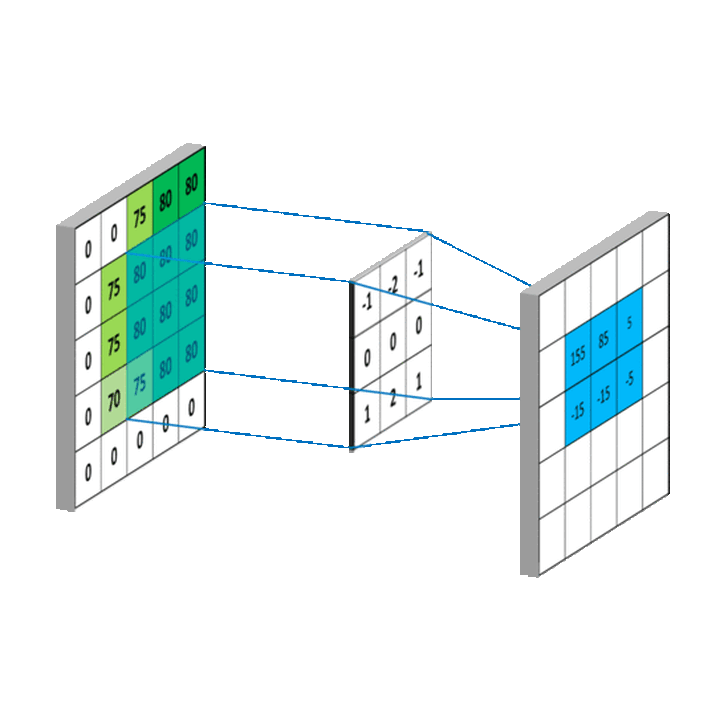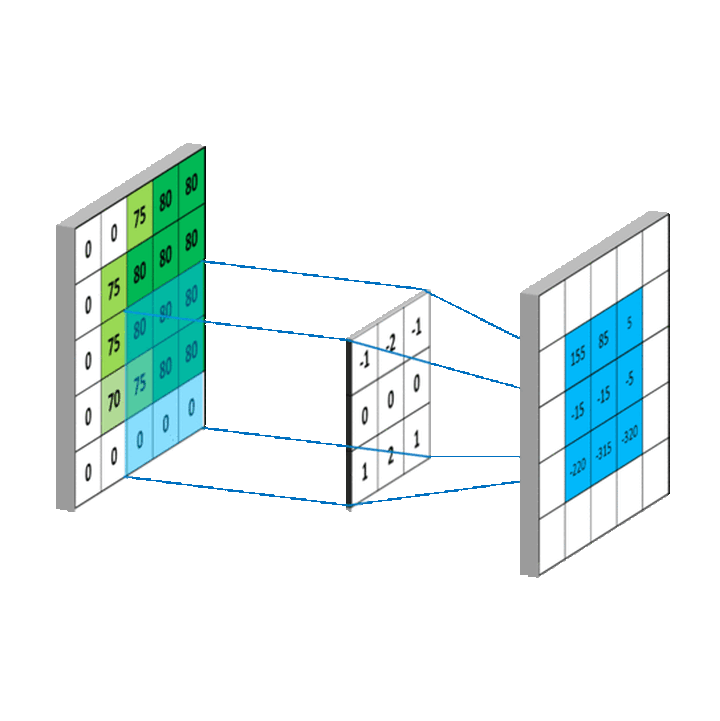
特别地，每一个特定的卷积核都可以提取图像中对应的特征信息

例如，一个形如这样的卷积核

\[ \begin{bmatrix} \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \\ \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \\ \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \end{bmatrix} \]

其卷积计算可以简化为 $(f * g)(u, v) = \frac{1}{c^2}\sum_i^c \sum_j^c f(i, j)$，即取卷积范围内9格数值的均值，从而起到平滑作用

又例如，一个形如这样的卷积核 \[ \begin{bmatrix} -1 & -1 & -1 \\ -1 & 9 & -1 \\ -1 & -1 & -1 \end{bmatrix} \]

其卷积计算可以简化为 $(f * g)(u, v) = f(u,v) - \sum_i^{i\neq u} \sum_j^{j\neq c} f(i, j)$，即将周围8格数值越小、中心点的数值越大（符合这种情况会形成一个点），其卷积结果越大。当卷积核滑动是，便形成了一条线，从而起到只提取线条的作用

在传统的图像处理任务中，这种卷积核都需要靠人工设计。而在CNN中，这个设计的过程则交给了神经网络来完成。

3.2.2. 前向传递

对于一个 $m \times n \times k$ 的输入，会被分拆成 $k$ 个1通道的矩阵，每个通道需要一个卷积核进行计算。由于每个通道的计算都是独立的，所以多通道的计算是并行的（也有说法认为每个通道的卷积核是共享的，但也需要所有通道都前向完成后才进行反向传播，所以即使是共享参数个通道的前向计算也是并行的）。每个矩阵单独进入卷积层后，最后对卷积层的输出进行求和合并。

而对于每个通道的输入，会用一个深度为 $k_c$ 的滤波器 $W$（即包含 $k_c$ 个卷积核）对其进行抽取，对应的，其输出为 $k_c$ 个像素矩阵。同时为了方便表示，将滤波器 $W$记为一个 $\{ c \times c \times k_c \times k \}$ 的数组，其中一个卷积核 $w$ 记为一个 $\{ c \times c \}$ 的数组。

至于该层的激活函数一般采用ReLu，其定义为 \[ \text{ReLu}(x) = \max(0, x) \] 这个激活函数的最大的特点是舍弃了小于0的部分、对大于0的部分不做修正。

由于在图像任务中，负值是没有意义的，所以这个函数是很适合用在图像任务中的，而且这个函数由于正值部分没有饱和区，所以其梯度消失问题会有所减轻，但会出现梯度爆炸的问题。关于该激活函数的更多特点可以参考这篇笔记：数学工具-激活函数

另外，由于卷积核的特征映射需要完全包含在像素矩阵内，所以卷积核只扫描到 $(m-c + 1) \times (n-c+1)$ 的区域，所以卷积层的输入输出是不等长的。有时候为了使输入输出等长，会采用一个trick——填充（padding）。常用的是往输出矩阵四周填充0，使其大小等同于输入矩阵，又称零填充（zero padding）

其次，由于等长的卷积计算是不降维的，有时为了能在卷积的同时进行降维，还会加入另外一个trick——步幅（stride）。步幅是一个参数，其控制卷积核窗口每滑动多少格才进行映射卷积。一个步幅为 $s$ 的滑动，零填充策略后的输出矩阵大小是输入矩阵大小的 $\frac{1}{s^2}$ 倍

最后，重新描述一遍卷积层的前向传递公式 \[ h_{t+1}(x) = \text{ReLu} \left (h_t(x) * W_t \cdot \vec 1\right) \] 其中 \[ h_{t}(x_{uv}) * W_t = \sum_{i} \sum_{j} h_{t, ij} \cdot W_{t,c-i,c-j} \] \[ \text{ReLu}(x) = \max(0, x) \]

$x \cdot \vec 1$ 表示对 $x$ 的最后一维求和，需要注意的是，求和后会默认压扁最后一个维度，即 $\{m \times n \times k_c \times 1 \} \rightarrow \{ m \times n \times k_c \}$

输入输出维度变化（有padding，无stride）：$h_t \rightarrow h_{t+1} : \{ m \times n \times k \} \rightarrow \{m \times n \times k_c\}$

可以看出卷积层实际上是把原图像由 $k$ 通道转换成 $k_c$ 通道，即所谓的将长和高变小，将深度变大。输出的每个通道称为一个特征图（feature map）

3.2.3. 反向传递

由于不包含偏置项 $b$（有时候也会加入偏置项），所以这一层的需要求两个梯度项 $\frac{\partial h_{t+1}}{\partial h_{t}}$ 和 $\frac{\partial h_{t+1}}{\partial W_t}$

先看 $\frac{\partial h_{t+1}}{\partial h_{t}}$ 的计算。

为了表示方便，令 $g_t(x) = h_t(x) * W_t,a(x) = x \cdot \vec 1$，则 $h_{t+1}(x) = \text{ReLu} \left (a(g_t(x))\right)$ \[ \frac{\partial h_{t+1}}{\partial h_{t}} = \frac{\partial h_{t+1}}{\partial a} \cdot \frac{\partial a}{\partial g_{t}} \cdot \frac{\partial g_{t}}{\partial h_{t}} \] 其中，

第一项，$\frac{\partial h_{t+1}}{\partial a}$ 就是求 $\text{ReLu}(x)$ 的导数，即 \[ \text{ReLu}'(x) = \left \{ \begin{array}{ll} 0 & ,x \leq 0 \\ 1 & ,x > 0 \end{array} \right . \]
第二项， $\frac{\partial a}{\partial g_{t}}$ 并非纯粹的数学操作，所以不能直接进行梯度求解。可以从数值流向进行分析。

对于运算 $x \cdot \vec 1$ ，这一步的求导就是按照各位置求和时的权值，加权分摊回各个位置即可。例如，数组 $[2,3]$，对应的梯度值计算就是 $\delta \cdot [0.4,0.6]$

定义数组权值为 $w' \in R^{1 \times k}$，则 \[ \delta \cdot \frac{\partial h_{t+1}}{\partial a} = \delta \cdot w' \]
第三项，$\frac{\partial g_{t}}{\partial h_{t}}$ 就是对卷积的求导了。省略求导过程，直接给出梯度表达式（卷积的求导推导起来有点麻烦，后面有时间再补吧） \[ \delta \cdot \frac{\partial g_{t}}{\partial h_{t}} = \delta * \text{rot180}(W_t) \] 其中，$\text{rot180}(x)$ 表示将 $x$ 旋转180度，如果前向传递时卷积计算对 $w$ 没有翻转，这里也不需要翻转

接下来，计算 $\frac{\partial h_{t+1}}{\partial W_t}$ \[ \frac{\partial h_{t+1}}{\partial h_{t}} = \frac{\partial h_{t+1}}{\partial a} \cdot \frac{\partial a}{\partial g_{t}} \cdot \frac{\partial g_{t}}{\partial W_{t}} \] 观察分解式，发现只有最后一项的计算与 $\frac{\partial h_{t+1}}{\partial h_{t}}$ 不一样，直接给出 $\frac{\partial g_{t}}{\partial W_{t}}$ 梯度表达式 \[ \delta \cdot \frac{\partial g_{t}}{\partial W_{t}} = \delta * h_t \]

3.3. 池化层

3.3.1. 前向传递

在几个卷积层后，通常会连接一个池化层。

池化层本质上也是一个 $p \times p$ 的过滤器，且其步幅也限定为 $p$。池化层有很多池化策略，常用的有最大池化和平均池化等。顾名思义，最大池化的过滤器的输出为感受野区域内的最大值，平均池化的过滤器的输出为感受野区域内的平均值，依次类推。

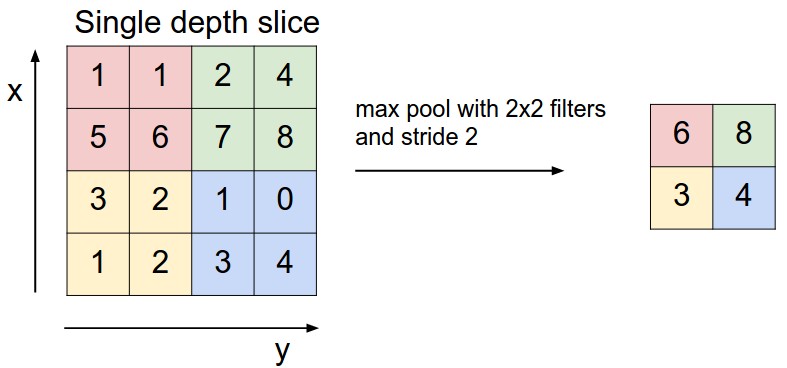
这一层的有两个作用：

降低复杂度。这个作用显而易见的。其输出降维输入的 $\frac{1}{p^2}$。复杂度降低有利于抑制噪声，降低信息冗余；提升模型的尺度不变性、旋转不变性；降低模型计算量等。
防止过拟合。你可以将过滤器其看做是一个非连续的激活函数。而非连续的激活函数是会改变原始数据的分布。例如最大池化会丢失部分信息，从而使分布改变。适当的改变分布则会降低过拟合程度。

最后给出池化层的定义式 \[ h_{t+1}(x) = \text{Pooling} (h_t(x)) \] 其中，

最大池化 \[ \text{Pooling} (X_k) = \left \{ \left \{ \max\{x_{k,ij}\mid pI< i \leq (p+1)I, pJ< j \leq (p+1)J\} \mid 0 \leq I < \frac{m}{p} \right \} \mid 0 \leq J < \frac{n}{p} \right \} \]
平均池化 \[ \text{Pooling} (X_k) = \left \{ \left \{ \frac{1}{p^2} \sum_i^{pI< i \leq (p+1)I} \sum_j^{pJ< j \leq (p+1)J} x_{k,ij} \mid 0 \leq I < \frac{m}{p} \right \} \mid 0 \leq J < \frac{n}{p} \right \} \]

一般来说，特征中只有部分信息比较有用时，选用最大池化，例如，图像存在噪声和很多无用的背景信息时，或者前景的亮度会高于背景时等；而特征中所有信息都比较有用时，使用平均池化，例如，网络最后几层，或者全连接层的前一层等。

输入输出维度变化：$h_t \rightarrow h_{t+1} : \{m \times n \times k_c\} \rightarrow \{\frac{m}{p} \times \frac{n}{p} \times k_c\}$

3.3.2. 反向传递

这一层不包含未知项（有时候也会加入偏置项），所以只有一个梯度项 $\frac{\partial h_{t+1}}{\partial h_{t}}$

同样的，这一步并非纯粹的数学操作，所以不能直接进行梯度求解。还是从数值流向角度进行分析

最大池化

池化后的数组中每一个值的梯度都由对应感受野区域内的最大值提供，所以池化前数组的最大值位置处的梯度为1，其余位置为0，写成公式表达为 \[ \delta_k \cdot \frac{\partial h_{t+1}}{\partial h_{t}} = \left \{ \left \{ \left\{\begin{array}{l}\delta_k &, (i,j)=\arg \max\{x_{ij}\mid I< i \leq I + p, J< j \leq J+p\} \\ 0 &, (i,j) \neq \arg \max\{x_{ij}\mid I< i \leq I + p, J< j \leq J+p\} \end{array}\right . \mid 0 \leq I < m \right \} \mid 0 \leq J < n \right \} \] 例如，对于池化前感受野数组 $[[1,2],[3,4]]$，最大值由 $(2,2)$ 处提供，所以对应的梯度为 $[[0,0],[0,1]]$。
平均池化

这个比较简单，由于池化后的数组中每个值都由感受野内均值提供，所以池化前数组都为感受野数值的均值，即 \[ \delta_k \cdot \frac{\partial h_{t+1}}{\partial h_{t}} = \left \{ \left \{ \frac{\delta_k}{p^2} \mid 0 \leq I < m \right \} \mid 0 \leq J < n \right \} \] 例如，对于池化前感受野数组 $[[1,2],[3,4]]$，对应的梯度为 $[[\frac{1}{4},\frac{1}{4}],[\frac{1}{4},\frac{1}{4}]]$。

3.4. Flatten层

3.4.1. 前向传递

这一层一般接到模型的输出层前，因为模型的最终输出为一维向量，而图像是一个高维的矩阵，所以需要先对输入压扁成一维向量。而这一层要实现的操作就是将一个多维的矩阵压缩为一个1维向量。这一步操作的是纯物理的，没有任何数学计算相关的操作。

定义函数 $\text{Flatten}_{m \times n \times k_c \rightarrow [m \times n \times k_c]}(x)$ 的操作为将矩阵从最后一维往上一个维度逐层压扁，直到压扁成一个一维的向量。故该层的函数定义为 \[ h_{t+1} = \text{Flatten}_{m \times n \times k_c \rightarrow [m \times n \times k_c]}(h_t) \] 实际操作中，压扁会因为横向还是纵向操作而产生不同的结果，具体可参考numpy的flatten操作的逻辑。

输入输出维度变化：$h_t \rightarrow h_{t+1} : \{ \frac{m}{p} \times \frac{n}{p} \times k_c \} \rightarrow \{[\frac{m}{p} \times \frac{n}{p} \times k_c]\}$

3.4.2. 反向传递

反向传递也纯物理操作，即将一个1维向量反向展开即可。

定义函数 $\text{UpSample}_{[m \times n \times k_c] \rightarrow m \times n \times k_c}(x)$ 的操作为将向量从第一维往下一个维度展开，直到展开成一个与 $h_t$ 的维度相同的矩阵，故该层的反向传递表达式为 \[ \delta \cdot \frac{\partial h_{t+1}}{\partial h_{t}} = \text{UpSample}_{[m \times n \times k_c] \rightarrow m \times n \times k_c}(\delta) \]

3.5. 全连接层

3.5.1. 前向传递

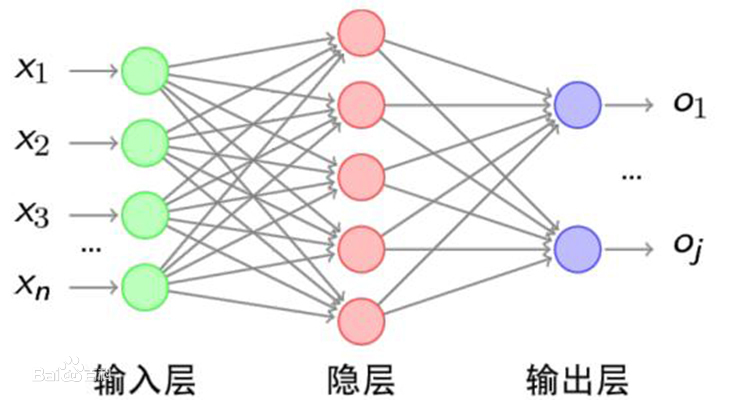
全连接层就是一层简单的DNN隐藏层，其一般作为CNN模型的输出层，输出每个图像的预测标签。

直接给出其定义 \[ h_{t+1}(x)=\text{softmax}(W_t \cdot h_{t}(x)+b_t) \] 其中， \[ \text{softmax}(x_i) = \frac{e^{x_i} }{\sum_j e^{x_j}} \] $\text{Flatten}_{m \times n \times k \rightarrow [m \times n \times k]}(x)$ 表示把一个3维的 $\{m \times n \times k \}$ 数组压扁成一个1维的 $\{[m \times n \times k]\}$ 向量

输入输出维度变化：$h_t \rightarrow h_{t+1} : \{ [\frac{m}{p} \times \frac{n}{p} \times k_c] \} \rightarrow \{K\}$

3.5.2. 反向传递

这一层一般就作为输出层，其实也没什么特别需要说的，都是老三样流程：设置损失函数然后求梯度。

损失函数方面，由于用了softmax，所以就用他的好基友交叉熵 $L(y,h_t(x)) = -y \ln h_{t}(x)$。

至于待求梯度项有三个 $\frac{\partial L}{\partial h_{t}}, \frac{\partial L}{\partial W_t}, \frac{\partial L}{\partial b_t}$

先看 $\frac{\partial L}{\partial h_{t}}$ 的计算。

同样的，为了表示方便，令 $g_t(x) = W_t \cdot h_{t}(x)+b_t$ \[ \frac{\partial L}{\partial h_{t}} = \frac{\partial L}{\partial g_{t}} \cdot \frac{\partial g_t}{\partial h_t} \] 其中，

第一项，$\frac{\partial L}{\partial g_{t}}$ 就是softmax交叉熵的求导了，即 \[ \frac{\partial L_i}{\partial g_{t,i}} =\left\{\begin{array}{l}g_{t,j}-1 &, i=j \\ g_{t,j} &, i \neq j\end{array}\right. \]
第二项，$\frac{\partial g_t}{\partial h_t} = W_t$

这一个梯度项搞定后，剩下的就比较简单了，下面直接给出计算结果 \[ \frac{\partial L}{\partial W_t} = \frac{\partial L}{\partial g_{t}} \cdot h_{t}(x) \]

\[ \frac{\partial L}{\partial b_t} = \frac{\partial L}{\partial g_{t}} \]