1. 输入输出

训练输入： \[ T=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中，

\(x\) 为特征域，\(x_i \in \mathbb{R}^{n},i =1,2,...,N\)
\(y\) 为标签域，\(y_i \in \{-1,+1\}\)

测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^n \] 测试输出： \[ Y'=\{y'_1,\cdots,y'_{N'}\},y_i' \in \{-1,+1\} \]

2. 模型效果

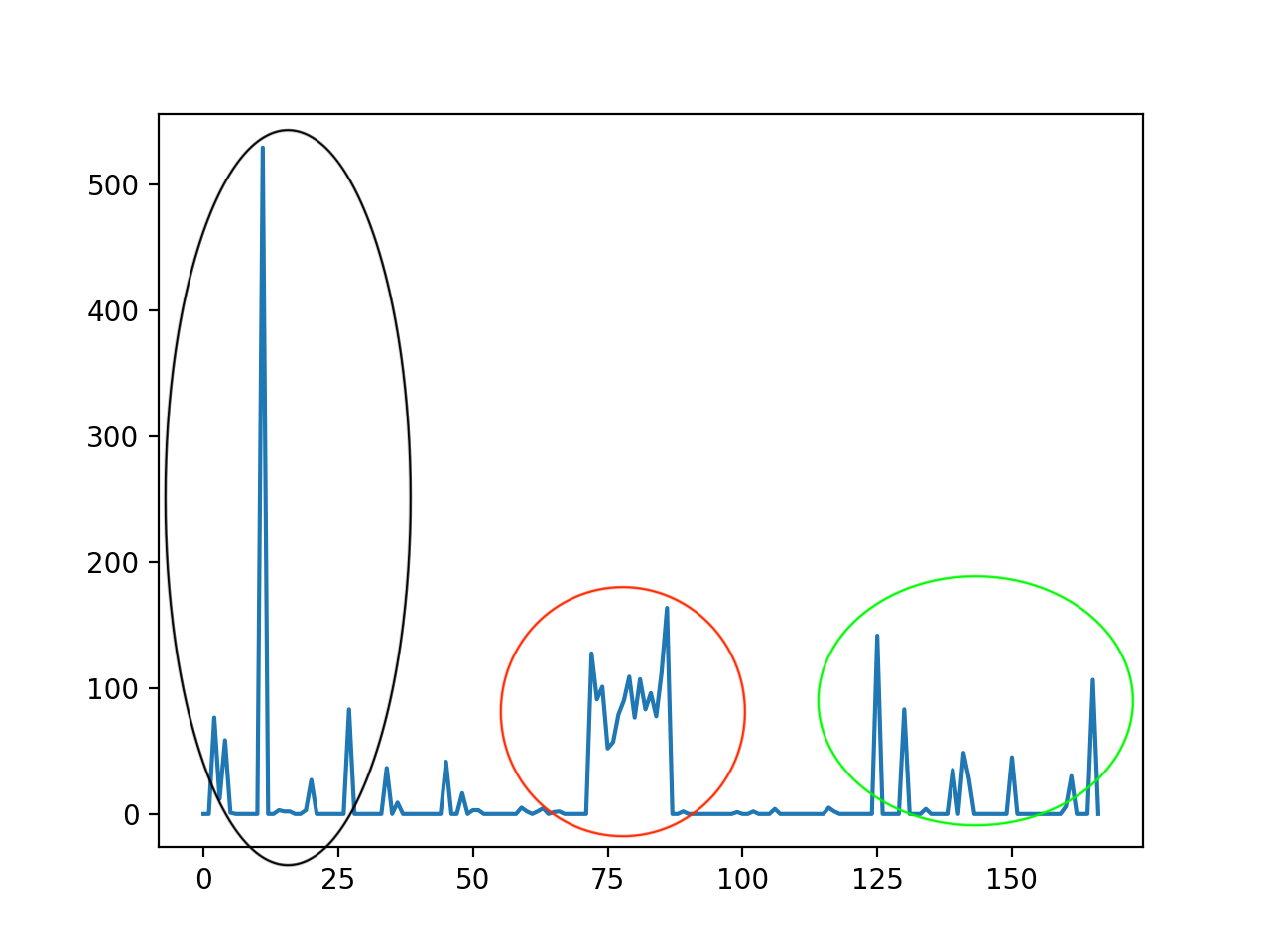
2.1. 训练效果

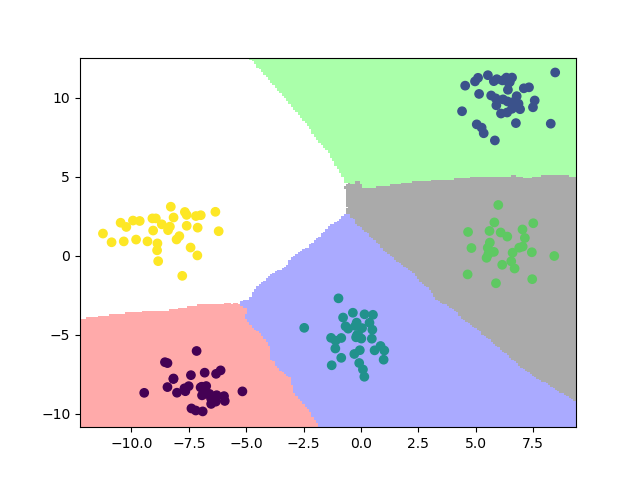
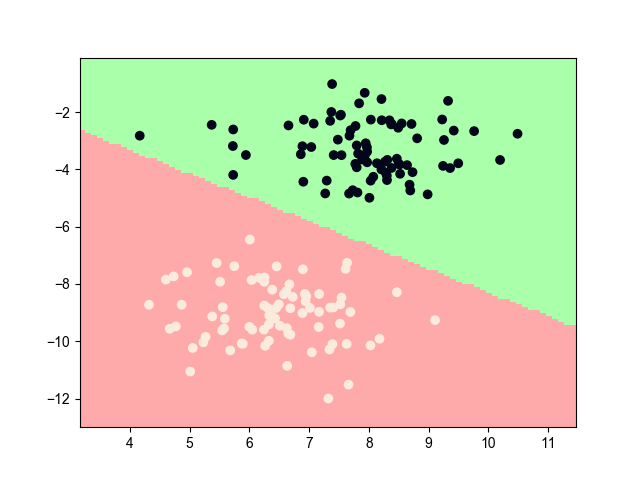
2.2. 最终效果

3. 模型推导

对于模型的推导，我一般都喜欢倒序推导，即从结果出发，从后面往前推，因为我觉得带着结果反推，会使每一步的意义变得更加清晰，更加自信地确认自己推导的过程是正确的

一般来说，如果只关注算法的编程实现，基本方法中的模型函数相当于程序的预测部分，学习算法中的参数更新相当于程序中的训练部分，而中间的学习策略是一段废话，只是告诉你算法的来龙去脉，可以直接忽略。

3.1. 基本方法

首先，我们假设 \(x_i \in \mathbf{R^2}\) ，即这是一个2维的向量。训练集 \(T\) 为一个3维的向量。

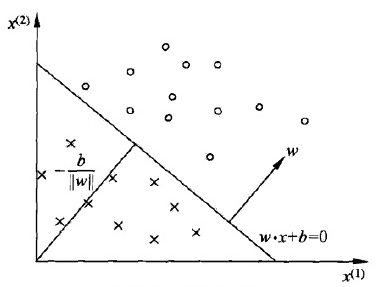
假设数据集是线性可分的，很自然地，我们可以想到可以使用一个如下的线性方程将数据集分成正负两部分 \[ w \cdot x + b = 0 \] 该线性方程对应特征域的一个超平面 \(S\)。其中，\(w\) 为 \(S\) 的法向量，\(b\) 为 \(S\) 的截距。

将特征域方向作为标签轴，将标签域方向的向量压缩成以符号的形式显示，如下图所示

即对所有 \(x \in \{ x_i|y_i=1\}\) 满足 \(w \cdot x + b > 0\)， \(x \in \{ x_i|y_i=-1\}\) 满足 \(w \cdot x + b < 0\)，即感知机模型的表达式为 \[ f(x)=\mathrm{sign}(w \cdot x + b ) \]

3.2. 学习策略

问题转化为如何求未知变量 \(w\) 和 \(b\)，但我们并不能直接求取上述两个未知变量。

为此，我们需要计算训练集中每一个点的误差值，我们可以通过定义一个损失函数来体现这个误差值。当损失函数达到最小值时，此时的 \(w\) 和 \(b\) 即为所求的未知变量。

因此，有两种损失函数的选择：一是计算所有误分类点的数量，但这个函数是离散非连续可导的，不易优化，pass掉；一是计算每个误分类点到 \(S\) 的距离，这个感觉靠谱，可以采用。

首先，为什么只计算误分类的点？因为感知机认为已经分类正确的数据没有参考价值，只需要优化误分类的点即可，所以感知机是误分类驱动的算法。对于所有误分类的点，满足如下条件 \[ -y_i(w \cdot x_i + b) > 0 \] 误分类点集 \(M\) 中每个点到 \(S\) 的距离为 \[ -y_i \cdot \frac{1}{||w||} (w \cdot x_i + b) \] 其中，\(||w||\) 为 \(w\) 的 \(L_2\) 范数

又所有误分类点到 \(S\) 的总距离即为损失函数，可得 \[ L(w,b)=- \sum_{x_i \in M}y_i (w \cdot x_i + b) \] 特别地，\(\frac{1}{||w||}\) 被忽略了（我们称原来的函数值为几何间隔，而忽略\(L_2\)范数的函数值为函数间隔）。因为\(L_2\)范数恒为正，不影响损失函数的正负判断，而损失函数优化的目的是使误分点为0，其判断依据完全由函数值的正负决定，而与该值的大小无关，故忽略 \(L_2\) 范数可以极大地简化计算。

3.3. 学习算法

问题进一步转化为如何求取损失函数的最小值。

我们可以使用随机梯度下降法逐渐逼近这个最小值。分别对未知变量 \(w\) 和 \(b\) 求其梯度值 \[ \nabla_w L(w,b) = - \sum_{x_i \in M} y_i x_i \\ \nabla_b L(w,b) = - \sum_{x_i \in M} y_i \] 对于任一时刻的任一误分点，对 \(w\) 和 \(b\) 进行如下更新 \[ w \leftarrow w + \eta y_i x_i \\ b \leftarrow b + \eta y_i \] 其中，\(\eta(0<\eta \leq 1)\) 为学习的步长，即学习率。

随机初始化未知变量 \(w_0\) 和 \(b_0\) ，不断经过上诉的迭代运算，直到误分点为0或超过预设的迭代次数，模型学习结束。

对于学习过程，可以解释为：当一个点被误分后，固定分类正确的一端，而旋转分类错误的一端，使得误分点被归类为正确的点。

4. Novikoff定理

对于 \(\hat{w} = (w^T, b)^T, \hat{x}=(x^T,1)^T\)，则 \(\hat{w} \cdot \hat{x} = w \cdot x + b\) ，不加证明地给出以下定理

对于线性可分的训练集，存在满足条件的 \(||\hat{w}||=1\) 的超平面 \(\hat{w} \cdot \hat{x}\) 将训练集完全分开，且存在 \(\gamma > 0\)，对所有的 \(i=1,2,...,N\)，有 \[ y_i(\hat{w} \cdot \hat{x}) \geq \gamma \]
令 \(R=\max_{1 \leq i \leq N} ||\hat{x}||\)，则误分类次数 \(k\) 满足 \[ k \leq (\frac{R}{\gamma})^2 \]

定理表明，误分类次数是有上界的，可以通过有限的次数将训练集正确地分开成两部分。

5. 对偶形式

上面的推导为原始形式，在特征空间的维度远大于数据集大小时，为了降低每次迭代的运算量，可以采用其对偶形式

对偶形式就是将 \(w,b\) 分别表示为 \[ w = \sum_{i=1}^N \alpha_i y_i x_i \\ b = \sum_{i=1}^N \alpha_i y_i \] 感知机模型转化为 \[ f(x) = \mathrm{sign}(\sum_{i=1}^N \alpha_i y_i x_i \cdot x + b) \] \(w,b\) 每次迭代的更新转化为 \[ \alpha_i \leftarrow \alpha_i + \eta \\ b \leftarrow b + \eta y_i \] 为了减少计算量，预先计算并保存一个Gram矩阵 \[ G=[x_i \cdot x_j]_{N \times N} \]