概率潜在语义分析(probabilistic latent semantic analysis,PLSA),也称概率潜在语义索引(PLSI),是一种利用概率生成模型对文本集合进行话题分析的无监督学习方法。
样本随机,参数虽未知但固定,所以PLSA属于频率派思想。
1. 模型推导
这一部分主要是根据李航书中的公式进行推导的,但书中一些地方感觉描述不太清晰,故有很多存疑的地方
1.1. 基本定义
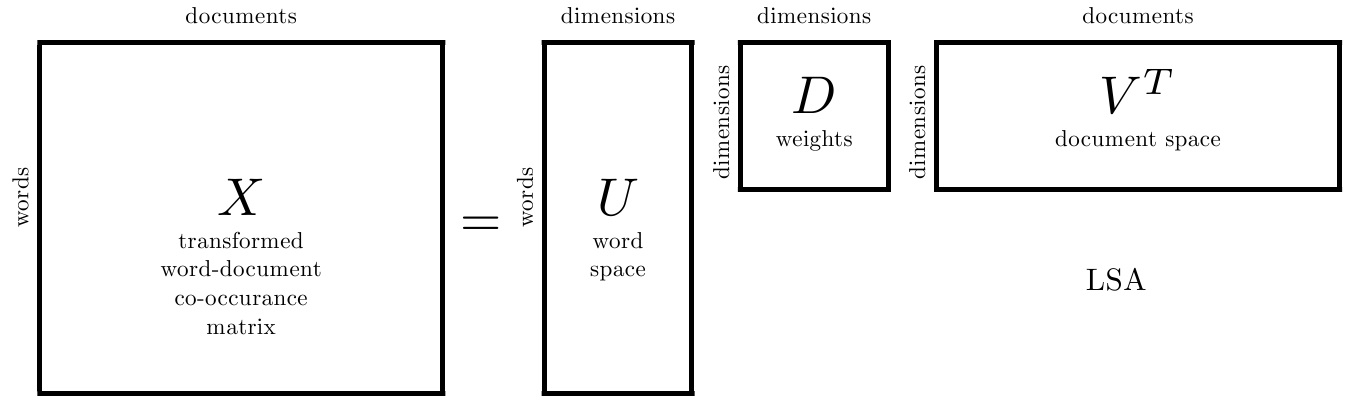
首先,从名字可以看出,PLSA是基于LSA的模型,两者最大的区别是PLSA是概率模型,而LSA是非概率模型
更进一步的,LSA模型对文本空间分解成若干个矩阵,而PLSA用概率分布理论对各矩阵进行了装饰。在后面提到的共现模型中,可以更加直接的体现了这种矩阵与概率分布的对应关系。
为了方便描述,首先给出如下符号的定义
- 文本集合 \(D=\{d_1,d_2,\cdots,d_N\}\),其中,\(N\) 为文本个数,概率分布\(P(d)\)表示生成文本\(d\)的概率
- 预设的话题集合 \(Z=\{z_1,z_2,\cdots,z_K\}\),其中,\(K\) 为预设的话题个数,条件概率分布\(P(z|d)\)表示文本\(d\)生成话题\(z\)的概率
- 单词集合 \(W=\{w_1,w_2,\cdots , w_M\}\),其中,\(M\) 为所有文本出现的单词个数,条件概率分布\(P(w|z)\)表示话题\(z\)生成单词\(w\)的概率
由上述变量,可以组合成模型的单词-话题-文本三元组 \((w,z,d)\) ,其中可观察的是单词-文本二元组 \((w,d)\),隐变量为 \(z\) ,用 \(n(w,d)\) 表示 \((w, d)\) 出现的次数,则共现数据 \(T\) (即输入的训练语料集)的生成概率为所有的 \((w,d)\) 生成概率的乘积,即 \[ P(T)=\prod_{(w, d)} P(w, d)^{n(w, d)} \] 按照对 \(P(w, d)\) 的不同定义,又有两种概率公式上相互等价的模型实现——生成模型与共现模型
1.1.1. 生成模型
生成模型认为,文本由话题决定,话题由单词决定,更加具体的:
依据概率分布\(P(d)\),从文本集合中随机选取一个文本\(d\),共生成\(N\)个文本;
在文本\(d\)给定条件下,依据条件概率分布\(P(z|d)\),从话题集合随机选取一个话题\(z\),共生成\(L\)个话题,这里\(L\)是文本长度
文本长度这个值应该理解为单词数量?但根据下面公式含义,这个值应该为话题数量?
在话题\(z\)的给定条件下,依据条件概率分布\(P(w|z)\),从单词集合中随机选取一个单词\(w\)
即下图所示关系
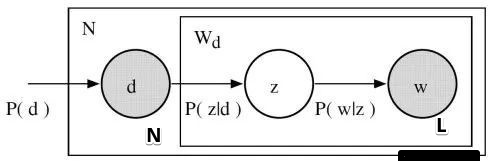
写成公式表达为
\[ \begin{aligned} P(w, d) &=P(d) P(w \mid d) \\ &=P(d) \sum_{z} P(w, z \mid d) \\ &=P(d) \sum_z P(z \mid d) P(w \mid z) \end{aligned} \]
其中,上述推导中假设在话题\(z\)给定条件下,单词\(w\)与文本\(d\)是条件独立的,即: \[ P(w, z \mid d)=P(z \mid d) P(w \mid z) \]
1.1.2. 共现模型
共现模型认为话题由文本和单词共同决定的,即下图所示关系
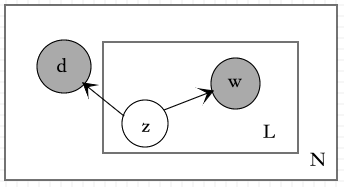
写成公式表达为
\[ \begin{aligned} P(w, d) &=\sum_{z \in Z} P(z) P(w, d \mid z) \\ &=\sum_{z \in Z} P(z) P(w \mid z) P(d \mid z) \end{aligned} \]
其中,上述推导中假设在话题\(z\)给定条件下,单词\(w\)与文本\(d\)是条件独立的,即: \[ P(w, z \mid d)=P(w \mid z) P(d \mid z) \]
注意,这跟生成模型的独立性假设是不一样的
可以观察到上述概率表达式的形式与SVD分解后的矩阵形式是类似的,故可以给出两者的弱对应关系: \[ \begin{aligned} X^{\prime} &=U^{\prime} \Sigma^{\prime} V^{\prime \top} \\ X^{\prime} &=[P(w, d)]_{M \times N} \\U^{\prime} &=[P(w \mid z)]_{M \times K} \\ \Sigma^{\prime} &=[P(z)]_{K \times K} \\ V^{\prime} &=[P(d \mid z)]_{N \times K} \end{aligned} \]
1.2. 学习算法
从两种模型的概率图可以直观的看出,生成模型是非对称的,而共现模型是对称的,由于两者的形式不同,故其学习算法也不同
下面以生成模型的学习算法为例
包含了隐变量的极值求解,熟悉的味道,熟悉的配方,于是又到了熟悉的三板斧流程——EM算法出马了
1.2.1. 极大似然函数
首先求完全数据的极大似然函数 \[ \begin{aligned} L &=\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \log P\left(w_{i}, d_{j}\right) \\&=\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \log \left[P\left(d_{j}\right) \sum_{k=1}^{K} P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)\right] \\&=\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right)\left\{\log P\left(d_{j}\right)+\log \left[\sum_{k=1}^{K} P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)\right]\right\} \\&=\sum_{i=1}^{M} \sum_{j=1}^{N}\left\{n\left(w_{i}, d_{j}\right) \log P\left(d_{j}\right)+n\left(w_{i}, d_{j}\right) \log \left[\sum_{k=1}^{K} P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)\right]\right\} \\&=\sum_{j=1}^{N} n\left(d_{j}\right) \log P\left(d_{j}\right)+\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \log \sum_{k=1}^{K} P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right) \\&= \sum_{j=1}^{N} n\left(d_{j}\right)\left(\log P\left(d_{j}\right)+\sum_{i=1}^{M} \frac{n\left(w_{i}, d_{j}\right)}{n\left(d_{j}\right)} \log \sum_{k=1}^{K} P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)\right) \end{aligned} \]
李航书中貌似缺少了 \(P\left(d_{j}\right)\) 这一项?
其中,\(n\left(d_{j}\right) = \sum_{i=1}^{M} n\left(w_{i}, d_{j}\right)\),表示文本 \(d_j\) 中的单词个数
1.2.2. E Step
计算Q函数
Q函数为完全数据的对数似然函数对不完全数据的条件分布的期望,即 \(Q=\sum_z \log P(w,d) P(z|w_i,d_j)\),继续展开为 \[ Q=\left\{\sum_{j=1}^{N} n\left(d_{j}\right)\left[\log P\left(d_{j}\right)+\sum_{i=1}^{M} \frac{n\left(w_{i}, d_{j}\right)}{n\left(d_{j}\right)} \sum_{k=1}^{K}\log P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)\right]\right\} P\left(z_{k} \mid w_{i}, d_{j}\right) \]
上面式子 \(P\left(z_{k} \mid w_{i}, d_{j}\right)\) 是在括号外的,即其下标i和j不属于括号内的求和循环中的,结合Q函数的定义,括号内的求和循环属于 \(\log P(w,d)\),所以应该表示为 \(P\left(z_{k} \mid w_{i'}, d_{j'}\right)\) 更加准确,但下面Q函数的简化中, \(P\left(z_{k} \mid w_{i}, d_{j}\right)\) 居然又被合并到内循环中了,书中也没给出具体的推导过程,不知道上下两步是如何转换的?
另外,书中的 \(\sum_{k=1}^{K}\) 这一项原本是提到花括号外面了,但这一步中 \(P\left(d_{j}\right)\) 这一项还没被去掉,所以私以为这一项不能提到外面
由于 \(P\left(d_{j}\right)\) 的计算不带有未知参数,可以忽略,则 \(Q\) 函数可以简化为 \(Q'\) 函数 \[ Q^{\prime}=\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \sum_{k=1}^{K} P\left(z_{k} \mid w_{i}, d_{j}\right) \log \left[P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)\right] \] 其中,\(P(z_k|d_j)\)和\(P(w_i|z_k)\)由上一步迭代得到,\(P\left(z_{k} \mid w_{i}, d_{j}\right)\) 可以根据贝叶斯公式计算:
\[ \begin{aligned} P\left(z_{k} \mid w_{i}, d_{j}\right) &= \frac{P(w_i,d_j,z_k)}{\sum_{l=1}^{K}P(w_i,d_j,z_l)} \\ &=\frac{P\left(w_{i} \mid d_j, z_{k}\right) P\left(z_{k} \mid d_{j}\right) P(d_j)}{\sum_{l=1}^{K} P\left(w_{i} \mid d_j, z_{l}\right) P\left(z_{l} \mid d_{j}\right) P(d_j)} \\ &= \cdots \\ &=\frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{\sum_{l=1}^{K} P\left(w_{i} \mid z_{l}\right) P\left(z_{l} \mid d_{j}\right)} \end{aligned} \]
1.2.3. M Step
极大化Q函数
此时,变量为 \(P(z_k|d_j)\)和\(P(w_i|z_k)\) ,又两者为概率函数,故满足约束条件 \[ \begin{array}{l} \sum_{i=1}^{M} P\left(w_{i} \mid z_{k}\right)=1, k=1,2, \ldots, K \\ \sum_{k=1}^{K} P\left(z_{k} \mid d_{j}\right)=1, j=1,2, \ldots, N \end{array} \]
处理带约束的极值问题,老规矩,上拉格朗日。
引入拉格朗日乘子 \(\tau_{k}\) 和 \(\rho_{j}\) ,定义拉格朗日函数: \[ \Lambda=Q^{\prime}+\sum_{k=1}^{K} \tau_{k}\left(1-\sum_{i=1}^{M} P\left(w_{i} \mid z_{k}\right)\right)+\sum_{j=1}^{N} \rho_{j}\left(1-\sum_{k=1}^{K} P\left(z_{k} \mid d_{j}\right)\right) \]
分别对 \(P(z_k|d_j)\)和\(P(w_i|z_k)\) 求偏导,并令其为0,从而得到: \[ \begin{array}{c} \sum_{j=1}^{N} \frac{n\left(w_{i}, d_{j}\right) P\left(z_{k} \mid w_{i}, d_{j}\right)}{P\left(w_{i} \mid z_{k}\right)}-\tau_{k}=0 \Rightarrow \\ \left[\sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) P\left(z_{k} \mid w_{i}, d_{j}\right)\right]-\tau_{k} P\left(w_{i} \mid z_{k}\right)=0 \\ i=1,2, \ldots, M \\k=1,2, \ldots, K \end{array} \]
\(\Lambda\) 中, \(P(z_k|d_j)\)和\(P(w_i|z_k)\) 是对称,所以根据其对称性可得 \[ \begin{array}{c} {\left[\sum_{i=1}^{M} n\left(w_{i}, d_{j}\right) P\left(z_{k} \mid w_{i}, d_{j}\right)\right]-\rho_{j} P\left(z_{k} \mid d_{j}\right)=0} \\j=1,2, \ldots, N \\ k=1,2, \ldots, K \end{array} \]
解方程消去 \(\tau_{k}\) 和 \(\rho_{j}\) ,解得 \[ P\left(w_{i} \mid z_{k}\right)=\frac{\sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) P\left(z_{k} \mid w_{i}, d_{j}\right)}{\sum_{m=1}^{M} \sum_{j=1}^{N} n\left(w_{m}, d_{j}\right) P\left(z_{k} \mid w_{m}, d_{j}\right)} \]
\[ P\left(z_{k} \mid d_{j}\right)=\frac{\sum_{i=1}^{M} n\left(w_{i}, d_{j}\right) P\left(z_{k} \mid w_{i}, d_{j}\right)}{n\left(d_{j}\right)} \]
2. references
《统计学习方法》18章,李航