1. 输入输出

Input:

观测变量 \[ X= \{x_1, x_2, ..., x_m\},x_i \in \mathbb{R}^n \] Output:

每一个 $x$ 对应的隐变量 $Z$ 概率分布函数 \[ Z= \{z_1, z_2, ..., z_m\} \]

2. 模型推导

2.1. 基本定义

在之前的模型中，都只涉及到观测变量，我们对此进行推广，加入隐变量概念。

观测变量，即可以通过实验等直接记录下来的变量，在仅有观测变量的场合中， $X$ 仅服从一个分布，即对于每个 $x$ 的输出值都是相对固定的。

加入隐变量后， $X$ 服从多个分布，即每个 $x$ 会存在多个输出值，至于最终输出哪个输出值则服从另一个额外的分布。

举一个简单的抛硬币例子。

假设仅有一枚均匀的（正面朝上和反面朝上的概率是一样的）硬币，此时仅有观测变量。则每次抛硬币，正面朝上的概率都在0.5左右；

但如果假设有A和B两枚硬币，一枚均匀，一枚不均匀，每次以一定的概率让你选择其中的一枚硬币，则这个选择概率就是隐变量。此时，正面朝上的概率就会取决于你选择了哪枚硬币。但选哪枚硬币我们是不能直接观测。所以我们需要一个数学工具去求取这个选择概率。

这里会有一个矛盾的地方。由于我们不能直接得出隐变量的分布情况，所以我们只能通过观测变量来间接求取隐变量。但观测变量的真实输出情况又依赖于隐变量的分布情况。于是便陷入了一个”鸡先蛋先“的悖论。

EM算法的基本思想就是先假设一个初始值，求出一个初始的隐变量（E步），然后通过该隐变量求得一个极大的似然分布（M步）。通过不断循环E步和M步，直到算法收敛。

这种算法思想在前面的Kmeans算法中已经有所提及

可以看出，该算法对初始状态敏感。

特别地，$X$ 和 $Z$ 连在一起称为完全数据，仅有 $X$ 称为不完全数据。

2.2. 学习策略

2.2.1. 目标函数

假设观测变量 $X$ 与隐变量 $Z$ 各服从某一分布，即 \[ X \sim A(\theta) \]

\[ z_i \sim B(\theta,\theta_i) \]

为了表示简便，这里不妨假设所有的变量都是一维的，则变量的上标不再表示变量的维度，而表示为迭代轮次，例如，$x^{(i)}$ 表示第 $i$ 次迭代中对应的 $x$ 值

仅有观测变量时，其条件概率为 $p(x;\theta)$；但加入隐变量后，$p(x;\theta)$是很难优化的，但 $p(x,z;\theta)$ 是很好优化的，例如，聚类的时候，如果提前知道每个样本的类别，那优化每个类的中心就很简单了。

所以需要使条件概率变为 $p(x;\theta)=\sum_z p(x,z;\theta)$

这里，$p(x;\theta)$ 和 $p(x|\theta)$ 的记法是等价的

于是，极大似然估计为 \[ \begin{aligned} \ell(\theta) &=\sum_{i} \log p\left(x^{(i)} ; \theta\right) \\ &=\sum_{i} \log \sum_{z^{(i)}} p\left(x^{(i)}, z^{(i)} ; \theta\right) \\&=\sum_{i} \log \sum_{z^{(i)}} Q_{i}\left(z^{(i)}\right) \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_{i}\left(z^{(i)}\right)} \\& \geq \sum_{i} \sum_{z^{(i)}} Q_{i}\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_{i}\left(z^{(i)}\right)} \\ &=J(\theta) \end{aligned} \] 上式用到了一个Jensen不等式转换，这是因为原式中是和的对数，直接求导非常麻烦。由于我们最终是对原式求极大值，那么我们不妨求一个渐进下界，通过求下界的极大值来逼近原式的极大值。于是为了方便求导，我们将和的对数转化为对数的和。

这里介绍一下Jensen不等式。

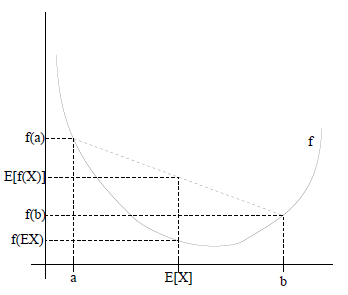
假设$f$是凸函数，$X$是随机变量，那么 $E[f(X)] \geq f(E[X])$，即函数的期望大于等于期望的函数。

特别地，如果$f$是严格凸函数，当且仅当$P(X = EX) = 1$，即$X$是常量时，上式取等号，即$E[f(X)] = f(EX)$。

对于任意实数 $x\in R$，如果二次导数 $f''(x) \geq 0$，则称 $f(x)$ 为凸函数

对于 $x$ 为向量，如果其hessian矩阵$H$是半正定的（$H \geq 0$），则称 $f(x)$ 为凸函数

如果 $f''(x) > 0 $ 或 $H > 0$，则称 $f(x)$ 为严格凸函数

Jensen不等式的函数图像如下

2.2.2. $Q$ 函数

上式中， $Q\left(z^{(i)};\theta\right) = J(\theta)$ 称为 $Q$ 函数，表示隐函数的期望值，具体含义为完全数据的对数似然函数 $\log P(X,Z|\theta)$ 对不完全数据 $X$ 在 $\theta^{(i)}$ 的条件下对未观测数据 $Z$ 的条件概率的分布 $P(Z|Y,\theta^{(i)})$ 期望

李航书中直接给出了 $Q$ 函数的定义，这里对其表达形式进行推导

由于 $\ell(\theta)$ 与 $J(\theta)$ 的梯度并不一致，所以我们不能严格通过 $J(\theta)$ 的极大值来确定 $\ell(\theta)$的极大值，退而求其次，取两者相等处作为最优解，当然这得到的是局部最优解。

于是，为了使上面的不等式取等号，需要令自变量为常数，即 \[ \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_{i}\left(z^{(i)}\right)}=c \] 则有 \[ \sum_{z} p\left(x^{(i)}, z^{(i)} ; \theta\right)=\sum_{z} Q_{i}\left(z^{(i)}\right) c \] 由于 $\sum_{z} Q_{i}\left(z^{(i)}\right)=1$，则 \[ \sum_{z} p\left(x^{i}, z^{(i)} ; \theta\right)=c \] 最终 \[ \begin{aligned} Q_{i}\left(z^{(i)}\right) &=\frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{\sum_{z} p\left(x^{(i)}, z ; \theta\right)} \\&=\frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{p\left(x^{(i)} ; \theta\right)} \\&=p\left(z^{(i)} \mid x^{(i)} ; \theta\right) \end{aligned} \]

在 $\log \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_{i}\left(z^{(i)}\right)} = \log p\left(x^{(i)}, z^{(i)} ; \theta\right) - \log Q_{i}\left(z^{(i)}\right)$ 中 $\log Q_{i}\left(z^{(i)}\right)$ 可以省去（为什么可以省去？），故得 \[ Q\left(Z;\theta\right) = E_Z\left[\log P(X,Z|\theta)|X,\theta^{(i)}\right] \\ =\sum_Z P(Z|X,\theta^{(i)}) \log P(X,Z|\theta) \]

Q函数可以简单理解为将对数似然函数中的 $\log \sum \cdot$ 转换为 $\sum \log \cdot$ 后再乘上一个 $P(Z|X,\theta^{(i)})$

2.2.3. 收敛性

在进行迭代求解之前，我们还需要证明一下目标函数 $\ell(\theta)$ 的收敛性

首先，可以知道 $\ell(\theta)$ 是一个有渐进上界的函数，所以只要证明函数是单调递增的即可，即 $\ell\left(\theta^{(t)}\right) \leq \ell\left(\theta^{(t+1)}\right)$

假设当前时刻的 $\ell\left(\theta^{(t)}\right)$ 为 \[ \ell\left(\theta^{(t)}\right)=\sum_{i} \log \sum_{z^{(i)}} Q_{i}^{(t)}\left(z^{(i)}\right) \frac{p\left(x^{(i)}, z^{(i)} ; \theta^{(t)}\right)}{Q_{i}^{(t)}\left(z^{(i)}\right)}=\sum_{i} \sum_{z^{(i)}} Q_{i}^{(t)}\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta^{(t)}\right)}{Q_{i}^{(t)}\left(z^{(i)}\right)} \] 则下一时刻的 $\ell\left(\theta^{(t+1)}\right)$ 为 \[ \begin{aligned} \ell\left(\theta^{(t+1)}\right) & = \sum_{i} \log \sum_{z^{(i)}} Q_{i}^{(t)}\left(z^{(i)}\right) \frac{p\left(x^{(i)}, z^{(i)} ; \theta^{(t+1)}\right)}{Q_{i}^{(t)}\left(z^{(i)}\right)} \\& \geq \sum_{i} \sum_{z^{(i)}} Q_{i}^{(t)}\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta^{(t+1)}\right)}{Q_{i}^{(t)}\left(z^{(i)}\right)} \\& \geq \sum_{i} \sum_{z^{(i)}} Q_{i}^{(t)}\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta^{(t)}\right)}{Q_{i}^{(t)}\left(z^{(i)}\right)} \\&=\ell\left(\theta^{(t)}\right) \end{aligned} \] 证毕

2.3. 学习算法

Init: 初始化参数 $\theta$

Repeat:

E step: 在给定参数下观测数据的后验概率，即固定参数 $\theta$ ，对于每个观测值，有 \[ Q_{i}\left(z^{(i)}\right):=p\left(z^{(i)} \mid x^{(i)} ; \theta\right) \]
M step: 重新计算新的估计值 $\theta$ \[ \theta:=\arg \max _{\theta} \sum_{i} \sum_{z^{(i)}} Q_{i}\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_{i}\left(z^{(i)}\right)} \]

Until: $\theta$ 变化值小于阈值 $\delta$

3. 一个例子

设 $X$ 服从标准分布，即 \[ X \sim N(\mu, \sigma) \] 每一个 $z_i$ 都服从二项分布，即 \[ z_i \sim B(\pi_i) \] 则E步中 \[ P(Z \mid X ; \theta)=\frac{P(X, Z ; \theta)}{\sum_{Z} P(X, Z ; \theta)}=\frac{\pi_{i} N\left(x ; \mu_{i}, \sigma_{i}\right)}{\sum_{k=1}^{m} \pi_{k} N\left(x ; \mu_{k}, \sigma_{k}\right)} \] M步中 \[ P(X, Z ; \theta)=P(Z ; \pi) P(X \mid Z ; \mu, \sigma)=\pi_{i} N\left(x ; \mu_{i}, \sigma_{i}\right) \]