数学基础数学工具

数学基础

发布日期: 2021-05-25

更新日期: 2022-08-10

文章字数: 5.8k

阅读时长: 24 分

阅读次数:

马尔科夫链蒙特卡罗（Markov Chain Monte Carlo，MCMC）

从名称上可以看出，该方法可以拆分为蒙特卡罗和马尔科夫链两种方法

传统的蒙特卡罗法是一种采用随机抽样的方式来近似求解求和或积分计算问题，但每次抽样都是是独立，只能解决单一变量问题；马尔科夫链是一种特殊的事件转换序列。于是两者结合，就可以用来解决多元变量的求和或积分计算问题。

1. 蒙特卡罗方法

1.1. 基本定义

蒙特卡罗原来是一个赌场的名称，所以说这个方法的本身就包含着赌博、碰运气的意思

蒙特卡罗法的原理很简单，为了方便描述，这里假设一个二维空间，其总面积为 $S'$，空间中有一待求区域，其面积为 $S$ ，空间中随机采集 $m$ 个点，如果采集到的点落在待求区域上的数量为 $n$，则待求区域的面积近似为 $S \approx \frac{n}{m}S'$

重用的方法有直接抽样法、接受-拒绝抽样法、重要性抽样法

接受-拒绝抽样法、重要性抽样法适合于概率密度函数复杂（如密度函数含有多个变量，各变量相互不独立，密度函数形式复杂），不能直接抽样的情况。

1.2. 具体方法

1.2.1. 直接抽样法

上述例子就是一个最简单的直接抽样法，下面推广至一般情况

面积计算问题可以转换为积分计算问题 \[ S = \int_a^b h(x) dx \] 假设抽样在 $[a,b]$ 区间内是均匀分布的，则采用 $n$ 次抽样 $\{x_1,\cdots x_n\}$ 的均值 $h(x_0)$ 代表 $[a,b]$ 区间上所有的 $h(x)$ 的值，则积分计算为 \[ S \approx \frac{b-a}{n} \sum_{i=1}^n h(x_i) \] 继续推广至抽样在 $\mathcal{X}$ 中以概率分布 $p(x)$ 抽样 $n$ 次的情况

不妨将 $h(x)$ 分解为一个函数 $f(x)$ 与概率密度函数 $p(x)$ 的形式，即 $h(x) = f(x) p(x)$，则上述积分计算变为 \[ S= \int_{\mathcal{X}} h(x) \mathrm{d} x=\int_{\mathcal{X}} f(x) p(x) \mathrm{d} x=E_{p(x)}[f(x)] \approx \frac{1}{n} \sum_{i=1}^{n} f\left(x_{i}\right) \]

$\int_{\mathcal{X}} f(x) p(x) \mathrm{d} x$ 就是统计学上关于 $x$ 的概率密度函数的期望计算公式

上述式子就是直接抽样法的一般形式，也适用于离散型的期望计算

可以使用一般形式去验证连续型均匀分布抽样的情况

均匀分布下，$p(x) = \frac{1}{b-a}$

则 $f(x) = \frac{h(x)}{p(x)} = (b-a)h(x)$

故 $\frac{1}{n} \sum_{i=1}^{n} f\left(x_{i}\right) = \frac{1}{n} \sum_{i=1}^{n} (b-a)h(x) = \frac{b-a}{n} \sum_{i=1}^n h(x_i)$

证毕。

1.2.2. 重要性采样法

有时候 $f(x)$ 可能很复杂，直接计算非常困难，可以使用重要性采样法

引入辅助概率分布 $s(x)$ ，原积分计算转换为 \[ S =\int_{\mathcal{X}} f(x) p(x) \mathrm{d} x = \int_{\mathcal{X}} \frac{f(x)}{s(x)} p(x) s(x) \mathrm{d} x \] 上式中，令 $w(x) = \frac{f(x)}{s(x)}$ 为重要性权重，则积分计算为 \[ S \approx \frac{1}{n} \sum_{i=1}^{n} w(x_i)p(x_i) \]

重要性采样法除了可以使计算方便，还一个重要的作用是时抽样后的样本更加接近真实样本

可以看出，抽样样本与真实样本的方差主要来源于 $f(x) = \frac{h(x)}{p(x)}$，所以 $h(x)$ 与 $p(x)$ 越接近，其方差越小，故只要找到一个合适的重要性权重 $w(x)$ ，抽样后的样本可以更加还原真实样本的分布情况

1.2.3. 接受-拒绝采样法

对于 $f(x)$ 非常复杂，甚至连表达式都可能给不出来的情况，可以采用接受-拒绝采样法

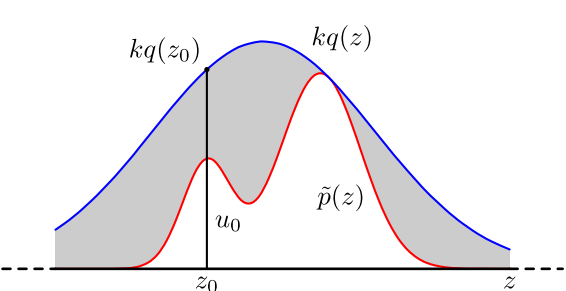
其基本想法是，找一个容易抽样的建议分布（proposal distribution）$q(x)$，其密度函数的$k$倍（$k$应尽可能小，理想情况为 $k=1$）大于等于想要抽样的概率分布的密度函数 $p(x)$，即 $kq(x)\geq p(x)$，然后按照一定的方法拒绝某些样本，以达到接近 $p(x)$ 分布的目的

效果如下图所示

采样过程：

Repeat:

从取值范围内采样得到样本 $z_0$
从均匀分布 $U(0,1)$ 中采样得到 $u$
如果 $u \leq \frac{p(z_0)}{kq(z_0)}$，则接受该次采样

Until: 采样数量达到 $n$ 个

这样采样的优点是容易实现，缺点是采样效率不高，特别到了高维区间，即使 ${p(z_0)}$和${kq(z_0)}$ 很接近，但两者涵盖体积差异也可能很大

2. 马尔科夫链

2.1. 基本定义

马尔科夫性：随机变量序列 $X=\{X_0,\cdots ,X_t,\cdots\}$ 中，$X_t$ 只依赖 $X_{t-1}$ ，而与其他变量无关的性质，即 \[ P ( X _ { t } | X _ { 0 } X _ { 1 } \cdots X _ { t - 1 } ) = P ( X _ { t } | X _ { t - 1 } ) , \quad t = 1,2 , \cdots \]
马尔科夫链：也称马尔科夫过程。具有马尔科夫性的随机序列。其中条件概率 $ P ( X _ { t } | X _ { t - 1 } )$ 为马尔科夫链的
齐次马尔科夫链：条件概率 $ P ( X _ { t } | X _ { t - 1 } )$ 与 $t$ 无关，即 \[ P ( X _ { t+s } | X _ { t - 1+s } ) = P ( X _ { t } | X _ { t - 1 } ) \] 常见序列为齐次马尔科夫链
n阶马尔科夫链：即 \[ P ( X _ { t } | X _ { 0 } X _ { 1 } \cdots X _ { t - 1 } ) = P ( X _ { t } | X _ { t - n }\cdots X_{t-1} ) , \quad t = 1,2 , \cdots \]

2.2. 离散状态马尔可夫链的一些定义

离散状态即状态集合空间 $S$ 是离散的

转移概率： $t-1$ 时刻处于状态 $i$ 转移到 $t$ 时刻处于状态 $j$ 的条件概率，即 \[ p_{ij} = p(X_t=i|X_{t-1}=j) \\ i\in S, j\in S \]
转移矩阵：记录 $t-1$ 时刻转移到 $t$ 时刻所有转移概率的矩阵，即 \[ P = [p_{ij}]_{i\in S, j\in S} \] 特别地，满足 $p_{ij} \geq 0,\sum_i p_{ij} = 1$ 也称为随机矩阵
状态分布：时刻为 $t$ 时，序列 $X$ 的状态分布，即 \[ \pi(t) = [\pi_i(t)]_{i\in S} \] 其中，$\pi_i(t) = P(X_t=i),i\in 0$

特别地，$i=0$ 的状态分布也称为初始状态分布；马尔科夫性也可表示为 \[ \begin{aligned} \pi(t) &= P \pi(t-1) \\ &=P^t \pi(0) \end{aligned} \] 其中，$P^t = P(X_t=i|X_0=j)$ 也称为 $t$ 步转移概率矩阵
平稳分布：满足 $\pi = P \pi$ 的状态分布。当序列处于平稳分布式，未来的任一时刻也将处于平稳分布

特别地，分布 $\pi=\left(\pi_{1}, \pi_{2}, \ldots\right)^{\top}$ 为$X$的平稳分布的充分必要条件是 $\pi=\left(\pi_{1}, \pi_{2}, \ldots\right)^{\top}$ 是下列方程组的解： \[ \begin{array}{c} x_{i}=\sum_{j} p_{i j} x_{j}, i=1,2, \ldots \\ x_{i} \geq 0, i=1,2, \ldots \\ \sum_{i} x_{i}=1 \end{array} \] 上式也是求平稳分布的一种方法

另外，马尔科夫链可能存在唯一、无穷多、0个平稳分布。

2.3. 连续状态马尔可夫链的一些定义

连续状态即状态集合空间 $S$ 是连续的

转移核：对应离散状态的转移概率，即 \[ P(x, A)=p(X_t=A|X_{t-1}=x) =\int_{A} p(x, y) \mathrm d y \\ x \in S, A \subset S \] 其中，$p(x,\bullet)$ 为概率密度函数，有时也称其为转移核，其满足 $p(x,\bullet) \geq 0,P(x,S)=1$
平稳分布：对应离散状态的平稳分布，即满足 \[ \pi ( y ) = \int p ( x , y ) \pi ( x ) \mathrm d x , \forall y \in S \] 或 \[ \pi ( A ) = \int p ( x , A ) \pi ( x ) \mathrm d x , \forall A \subset S \] 的状态分布

2.4. 若干性质

可约性

在状态空间$S$中，对于任意状态$i,j\in S$，如果存在一个时刻$t>0$，满足： \[ P\left(X_{t}=i \mid X_{0}=j\right)>0 \] 也就是说，时刻0从状态j出发，时刻t到达状态i的概率大于0，则称此马尔可夫链是不可约的（irreducible），否则称马尔可夫链是可约的（reducible）

直观上，一个不可约的马尔可夫链，从任意状态出发，当经过充分长时间后，可以到达任意状态。
周期性

在状态空间$S$中对于任意状态 $i\in S$，如果时刻0从状态i出发，返回状态i的的所有时长的集合 $\left \{t:P(X_{t}=i|X_{0}=i)> 0\right \}$的最大公约数是1，则称此马尔可夫链是非周期的（aperiodic），否则称马尔可夫链是周期的（periodic）。

直观上，一个非周期性的马尔可夫链，不存在一个状态，从这一个状态出发，再返回到这个状态时所经历的时间长呈一定的周期性，也就是说非周期性的马尔可夫链的任何状态都不具有周期性。
正常返

对于任意状态 $i,j\in S$，定义概率 $p_{ij}^{t}$ 为时刻0从状态j出发，时刻t首次转移到状态i的概率，即 $p_{ij}^{t}=P(X_{t}=i,X_{s}\neq i,s=1,2,\cdots ,t-1|X_{0}=j),t=1,2,\cdots$。若对所有状态 $i,j$都满足 $\lim_{t\rightarrow \infty}p_{ij}^{t}> 0$则称马尔可夫链是正常返的（positive recurrent）。

直观上，一个正常返的马尔可夫链，其中任意一个状态，从其他任意一个状态出发，当时间趋于无穷时，首次转移到这个状态的概率不为0。

定理：不可约、非周期且正常返的马尔可夫链，有唯一平稳分布存在。
遍历定理

若马尔可夫链是不可约、非周期且正常返的，则该马尔可夫链有唯一平稳分布$\pi=(\pi_{1},\pi_{2},\cdots )^T$ ，并且转移概率的极限分布是马尔可夫链的平稳分布 \[ \lim _{t \rightarrow \infty} P\left(X_{t}=i \mid X_{0}=j\right)=\pi_{i}, \quad i=1,2, \cdots, \quad j=1,2, \cdots \] 简化为 \[ \lim _{t \rightarrow \infty} P\left(X_{t}=i\right)=\pi_{i}, \quad i=1,2, \cdots \] 若$f(X)$是定义在状态空间上的函数， $E_{\pi }[f(X)]< \infty$则： \[ P\left\{\hat{f}_{t} \rightarrow E_{\pi}[f(X)]\right\}=1 \] 这里，$\hat{f}_{t}=\frac{1}{t} \sum_{s=1}^{t} f\left(x_{s}\right)$，$E_{\pi}[f(X)]=\sum_{i} f(i) \pi_{i}$ 是 $f(X)$关于平稳分布 $\pi=(\pi_{1},\pi_{2},\cdots )^T$的数学期望，$P\left \{\hat{f}_{t}\rightarrow E_{\pi }[f(X)]\right \}=1$表示 $\hat{f}_{t}\rightarrow E_{\pi }[f(X)],t\rightarrow \infty$ 几乎处处成立或以概率1成立。

直观上，满足相应条件的马尔可夫链，当时间趋于无穷时，马尔可夫链的状态分布趋近于平稳分布，随机变量的函数的样本均值以概率1收敛于该函数的数学期望。

样本均值可以认为是时间均值，数学期望是空间均值。

遍历定理表述了遍历性的含义：当时间趋于无穷时，时间均值等于空间均值。

遍历定理的三个条件：不可约、非周期、正常返，保证了当时间趋于无穷时达到任意一个状态的概率不为0。

理论上并不知道经过多少次迭代，马尔可夫链的状态分布才能接近平稳分布，在实际应用遍历定理时，取一个足够大的整数 $m$，经过$m$次迭代之后认为状态分布就是平稳分布，这时计算从第 $m+1$次迭代到第$n$次迭代的均值，即 \[ E_{\pi}[f(X)]=\frac{1}{n-m} \sum_{i=m+1}^{n} f\left(x_{i}\right) \] 称为遍历均值
可逆性

对于任意状态$i,j\in S$，对任意一个时刻$t$满足： \[ P\left(X_{t}=i \mid X_{t-1}=j\right) \pi_{j}=P\left(X_{t-1}=j \mid X_{t}=i\right) \pi_{i}, \quad i, j=1,2, \cdots \] 或简写为 \[ p_{i j} \pi_{j}=p_{j i} \pi_{i}, \quad i, j=1,2, \cdots \] 则称此马尔可夫链为可逆马尔可夫链（reversible Markov chain），上式又被称作细致平衡方程（detailed balance equation）。

直观上，如果有可逆马尔可夫链，那么以该马尔可夫链的平稳分布作为初始分布，进行随机状态转移，无论是面向过去还是面向未来，任何一个时刻的状态分布都是该平稳分布。

定理：满足细致平衡方程的状态分布 $\pi$ 就是该马尔可夫链的平稳分布

该定理说明，可逆马尔可夫链一定有唯一平稳分布

3. 马尔可夫链蒙特卡罗法

3.1. 基本想法

在进行推导前，先对问题进行如下假设：

假设多元随机变量 $x \in \mathcal{X}$，其概率密度函数为$p(x)$，$f(x)$为定义在 $x \in \mathcal{X}$上的函数，问题目标是获得概率分布$p(x)$的样本集合，以及求函数$f(x)$的数学期望 $E_{p(x)}[f(x)]$。

应用马尔可夫链蒙特卡罗法解决这个问题的想法步骤如下：

在随机变量$x$的状态空间$S$上定义一个满足遍历定理的马尔可夫链 $X=\left\{X_{0}, X_{1}, \ldots, X_{t}, \ldots\right\}$，使其平稳分布就是抽样的目标分布$p(x)$。
在这个马尔可夫链上进行随机游走，每个时刻得到一个样本。根据遍历定理，当时间趋于无穷时，样本的分布趋近平稳分布，样本的函数均值趋近于函数的数学期望。
当时间足够长时（时刻大于某个正整数$m$），在之后的时间（时刻小于等于某个正整数$n$，$n>m$）里随机游走得到的样本集合 $\left\{x_{m+1}, x_{m+2}, \ldots, x_{n}\right\}$ 就是目标概率分布的抽样结果，得到的函数均值（遍历均值）就是要计算的数学期望值: \[ \hat{E} f=\frac{1}{n-m} \sum_{i=m+1}^{n} f\left(x_{i}\right) \] 其中，到时刻$m$为止的时间段称为燃烧期。

上面步骤中，有以下问题需要解决：

如何定义马尔可夫链，保证马尔可夫链蒙特卡罗法的条件成立
如何确定收敛步数m，保证样本抽样的无偏性
如何确定迭代步数n，保证遍历均值计算的精度

针对以上问题，目前常见的有如下几种具体的解决方案

3.2. 具体算法

3.2.1. Metropolis-Hastings算法

3.2.1.1. 马链的定义

要保证马链具有平稳分布，最简单的方法就是保证其满足细致平衡方程 \[ \pi(x) q(x, x^{\prime}) = \pi(x^{\prime}) q(x^{\prime}, x) \] 其中，$q$ 是当前马链的转移矩阵

但是上式并不保证一定成立，所以不妨加入一个函数 $\alpha$ 满足 \[ \begin{array}{l} \alpha(x, x^{\prime})=\pi(x^{\prime}) q(x^{\prime}, x) \\ \alpha(x^{\prime}, x)=\pi(x) q(x, x^{\prime}) \end{array} \] 即可保证以下等式成立 \[ \pi(x) q(x, x^{\prime})\alpha(x, x^{\prime}) = \pi(x^{\prime}) q(x^{\prime}, x)\alpha(x^{\prime}, x) \] 于是MH算法对马链的转移矩阵的定义也呼之欲出了： \[ p\left(x, x^{\prime}\right)=q\left(x, x^{\prime}\right) \alpha\left(x, x^{\prime}\right) \] 其中，

$p\left(x, x^{\prime}\right)$ 为马尔可夫链的转移核，即 $p\left(x, x^{\prime}\right) = P \left(X_{t}=x \mid X_{t-1}=x^{\prime}\right)$ ，可以是离散型或连续型的
$q(x, x^{}) $ 为建议分布（proposal distribution），是马尔可夫链的另一个转移核，是不可约的，即其概率值恒不为0，同时是一个容易抽样的分布。
$\alpha\left(x, x^{\prime}\right)$ 为接受分布（acceptance distribution），其定义为 \[ \alpha\left(x, x^{\prime}\right)=\min \left\{1, \frac{p\left(x^{\prime}\right) q\left(x^{\prime}, x\right)}{p(x) q\left(x, x^{\prime}\right)}\right\} \]

特别地，上式定义可以转化为 \[ p\left(x, x^{\prime}\right)=\left\{\begin{array}{l} q\left(x, x^{\prime}\right), p\left(x^{\prime}\right) q\left(x^{\prime}, x\right) \geq p(x) q\left(x, x^{\prime}\right) \\ q\left(x^{\prime}, x\right) \frac{p\left(x^{\prime}\right)}{p(x)}, p\left(x^{\prime}\right) q\left(x^{\prime}, x\right)<p(x) q\left(x, x^{\prime}\right) \end{array}\right. \]

此时，转移核为$p(x,x^{\prime})$的马尔可夫链是可逆马尔可夫链(满足遍历原理)，其平稳分布就是$p(x)$，即要抽样的目标分布。

3.2.1.2. 马链的收敛

采用蒙卡罗特法的接受-拒绝抽样计算，直到马链收敛

更加具体的，假设上一时刻 $t-1$ 时处于状态 $x$ ，不妨先按建议分布 $q(x, x^{}) $ 抽样得到当前状态 $x^{\prime}$，取一均匀分布随机数 $u$ ，与接收分布 $\alpha\left(x, x^{\prime}\right)$ 进行比较，以此来决定是保留还是拒绝该次转移，即 \[ x_{t}=\left\{\begin{array}{l} x^{\prime}, u \leq \alpha\left(x, x^{\prime}\right) \\ x, u>\alpha\left(x, x^{\prime}\right) \end{array}\right. \]

3.2.1.3. 建议分布的确定

常采用以下两种定义：

假设建议分布是对称的，即对任意的$x$和 $x^{\prime}$ 有 \[ q\left(x, x^{\prime}\right) = q\left(x^{\prime}, x\right) \] 这样的建议分布称为Metropolis选择，也是Metropolis-Hastings算法最初采用的建议分布。这时，接受分布 $\alpha\left(x, x^{\prime}\right)$ 简化为 \[ \alpha\left(x, x^{\prime}\right)=\min \left\{1, \frac{p\left(x^{\prime}\right)}{p(x)}\right\} \] 特别地，有以下两个特例取值
- $q(x, x^{}) $ 为 $p\left( x^{\prime}, x \right)$ ，则其定义为多元正态分布，其均值为x，其协方差矩阵是常数矩阵
- $q(x, x^{}) $ 为 $q\left(x, x^{\prime}\right)=q\left(\left|x-x^{\prime}\right|\right)$，则称其为随机游走Metropolis算法，例如 \[ q\left(x, x^{\prime}\right) \propto \exp \left(-\frac{\left(x^{\prime}-x\right)^{2}}{2}\right) \]
Metropolis选择的特点是当 $x^{\prime}$ 与$x$接近时，$q(x, x^{}) $ 的概率值高，否则 $q(x, x^{}) $ 的概率值低。状态转移在附近点的可能性更大。
独立抽样。假设 $q(x, x^{}) $ 与当前状态x无关，即 $q\left(x, x^{\prime}\right) = q(x^{\prime})$ 。建议分布的计算按照 $q(x^{\prime})$ 独立抽样进行。此时，接受分布 $\alpha\left(x, x^{\prime}\right)$ 可以写成: \[ \alpha\left(x, x^{\prime}\right)=\min \left\{1, \frac{w\left(x^{\prime}\right)}{w(x)}\right\} \] 其中，$w\left(x^{\prime}\right)=p\left(x^{\prime}\right) / q\left(x^{\prime}\right), w(x)=p(x) / q(x)$

独立抽样实现简单，但通常收敛速度慢，通常选择接近目标分布$p(x)$的分布作为建议分布$q(x)$。

3.2.2. 单分量Metropolis-Hastings算法

在Metropolis-Hastings算法中，通常需要对多元变量分布进行抽样，联合抽样的计算量总是很大的。因此，可以对多元变量的每一变量的条件分布依次分别进行抽样，从而实现对整个多元变量的一次抽样，即单分量Metropolis-Hastings算法。

先进行如下定义

马链的状态矩阵 $x=(x_1,\cdots,x_k)^T$，其中，$x_j$ 表示第 $j$ 个分量，$x^{(i)}$ 表示马链在时刻 $i$ 的状态，$x_{j,i}$ 表示 $x^{(i)}$ 的第 $j$ 个分量，$x_{-j,i}$ 表示 $x^{(i)}$ 除去 $x_{j,i-1}$ 的所有值，即 $x_{-j,i}=(x_{1,i},\cdots,x_{j-1,i},x_{j+1,i-1},\cdots,x_{k,i-1})$ （这里，前一部分的上标是 $i$ ，是因为这些分量已经更新为时刻 $i$ 的分量了）
时刻$i-1$的第 $j$ 个分量的转移概率为 $p(x_{j,i-1},x^{\prime}_{j,i} | x_{-j,i})$ ，建议分布为 $q(x_{j,i-1},x^{\prime}_{j,i} | x_{-j,i})$，接受分布为 $\alpha(x_{j,i-1},x^{\prime}_{j,i} | x_{-j,i})$

其迭代过程将原始的MH算法中多元变量 $x^{(i)}$ 一起更新转换成循环对每一特征维度的单一分量 $x_{j,i}$ 单独更新即可

3.2.3. 吉布斯抽样（Gibbs sampling）

尽管可以采用单一分量的MH算是，但当状态矩阵的维度很高时，加上接受分布的存在，MH算法的计算效率仍然很低，由于一般情况下，条件概率比联合概率容易求取，因此是否可以用特征维度间的条件概率抽样来代替联合概率抽样，同时，是否可以不拒绝转移呢？这就是吉布斯抽样对MH算法的核心改进原理

其基本做法是，从联合概率分布定义满条件概率分布，依次对满条件概率分布进行抽样，得到样本的序列。

如果一个 $k$ 维状态的马链中，条件概率分布 $p(x_I|x_{-I})$ 中所有 $k$ 个变量全部出现，其中 $x_I = \{x_i,i\in I\},x_{-I}=\{x_i,i \notin I\},I \subset K = \{1,\cdots k\}$，则称这种条件概率分布为满条件分布

对于满条件分布，有 \[ p\left(x_{I} \mid x_{-I}\right)=\frac{p(x)}{\int p(x) \mathbf d x_{I}} \propto p(x) \] 及 \[ \frac{p\left(x_{I}^{\prime} \mid x_{-I}^{\prime}\right)}{p\left(x_{I} \mid x_{-I}\right)}=\frac{p\left(x^{\prime}\right)}{p(x)} \]

定义建议分布即为当前变量的满条件概率分布，即 \[ q\left(x, x^{\prime}\right) = p\left( x^{\prime}|x_{-j} \right) \] 其中，满条件概率分布可以按照其性质计算得到

此时，接受概率为 \[ \begin{aligned} \alpha\left(x, x^{\prime}\right) &=\min \left\{1, \frac{p\left(x^{\prime}\right) q\left(x^{\prime}, x\right)}{p(x) q\left(x, x^{\prime}\right)}\right\} \\ &=\min \left\{1, \frac{p\left(x_{-j}^{\prime}\right) p\left(x_{j}^{\prime} \mid x_{-j}^{\prime}\right) p\left(x_{j} \mid x_{-j}^{\prime}\right)}{p\left(x_{-j}\right) p\left(x_{j} \mid x_{-j}\right) p\left(x_{j} \mid x_{-j}^{\prime}\right)}\right\} \\ &=1 \end{aligned} \] 这意味着吉布斯采样对每次的结果都接受，没有拒绝

故最终马链的转移概率计算为 \[ p\left(x, x^{\prime}\right)= p\left( x^{\prime}|x_{-j} \right) \]

接下来马链的迭代按照单一MH算法中马链的迭代执行即可

可以证明，这样的抽样过程是在一个马尔可夫链上的随机游走，每一个样本对应着马尔可夫链的状态，平稳分布就是目标的联合分布。整体成为一个马尔可夫链蒙特卡罗法，燃烧期之后的样本就是联合分布的随机样本。

特别地，一般情况下，满条件分布可以计算出来的就采用吉布斯采用，不能计算出来的就采用单一的MH抽样