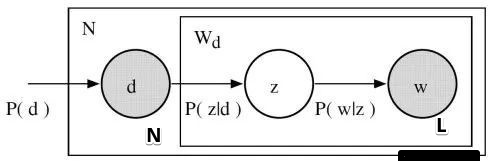
潜在语义分析(Latent Semantic Analysis,LSA),也称潜在语义索引(latent semantic indexing,LSI)是一种无监督学习方法,主要用于文本的话题分析。
1. 模型推导
1.1. 基本定义
文本任务中很多都涉及到语义相似度的计算,最简单就是利用向量空间模型(VSM),将文本转化为向量表示,然后将两个文本的向量表示的内积或标准化内积(余弦)值看做两个文本的间语义相似度。
如果采用单词向量空间表示文本向量,即每一个向量都应包含了所有输入文本的每一个单词的信息,即 \(X=[x_{ij}]_{m \times n}\),其中,\(m\) 是所有文本出现过的单词集合 \(W\) 的大小,\(n\) 是文本集合 \(D\) 的大小,\(x_{ij}\) 就是单词集合中的 \(w_i\) 在文本 \(d_j\) 中的权值表示。
这种方法的优点是模型简单,计算效率高(这是因为单词向量一般都是稀疏的,两个向量的内积计算只需在两者都不为0的维度上进行即可,所以计算量较少),但由于一词多义性和多词一义性,基于单词向量的相似度计算往往是不精确的(根本原因就是单词向量模型把每一个单词都当做是一个符号,一个单词作为一个维度,是实际上,现实中的单词与其他单词联动时会产生不同意思,而单词向量模型强行将两个单词当做是独立的,同一种语义的不同词语被当做不同维度分别计算了,或者强行将一个单词规定只能包含一种维度信息,不同语义的同一词语被当做一个维度进行计算了,从而导致计算的不准确)。
于是,主题模型就设想用一个话题向量模型来代替单词向量模型,而LSA的目标就是构建一条如下的等式 \[ X \approx TY \] 其中,\(X \in R^{m \times n}\) 为单词-话题矩阵(单词向量空间),\(T\in R^{m \times k}\) 为单词-话题矩阵(话题向量空间),\(Y\in R^{k \times n}\) 为话题-文本矩阵(文本在话题空间中的表示)
可以看出,LSA原理就是将n维的单词向量空间,通过线性变换,转换为k维话题空间的表示,使得,LSA前两文本的相似度表示为 \(x^{(i)} \cdot x^{(j)}\) ,LSA后两文本的相似度表示为 $ y{(i)}y{(j)}$
在上面3个矩阵中,\(X\) 是可以通过计算得到的,其一般使用TF-IDF计算得到,这种方法在这篇笔记中已经提及过,这里就不再赘述。
而 \(T\) 和 \(Y\) 是待求矩阵,可以通过以下算法求取。
传统的LSA算法,当有新文本加入时,上述的三个矩阵都要重新计算
1.2. 学习算法
1.2.1. 奇异值分解
LSA是将 $X $ 转换为 \(T\) 和 \(Y\) 的表示,实际上就是做矩阵分解,既然是矩阵分解,很自然地,就会想到使用截断SVD
首先给出截断SVD的目标函数 \[ X \approx U_k \Sigma_k V_k^T \] 求解各个矩阵的方法在这篇笔记中已经提及过,这里也不再赘述。
在SVD中,\(U\) 和 \(V\) 表示旋转量,\(\Sigma\) 表示缩放量,在LSA中,其物理含义表示如下
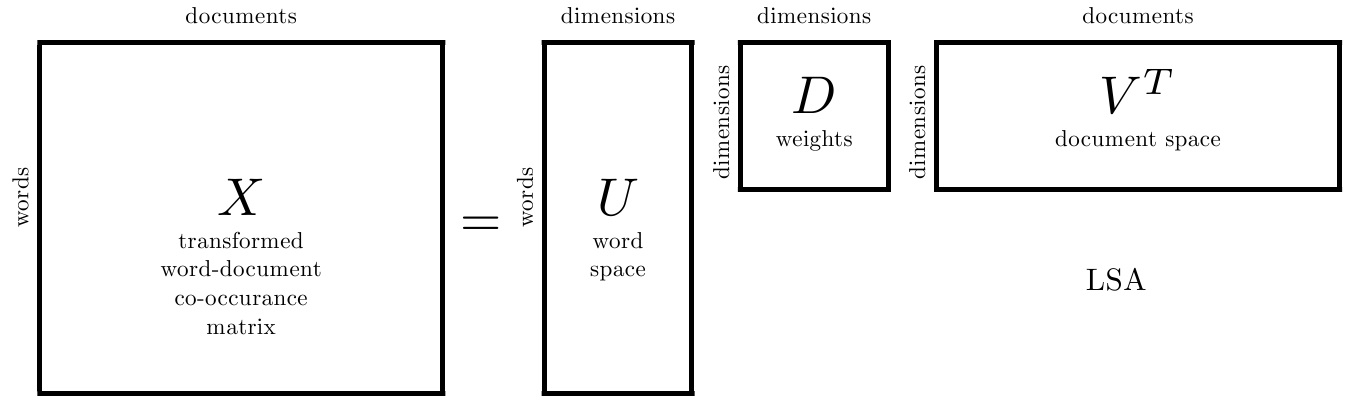
\(U\) 中每一行表示意思相关的一类词,\(V^T\) 中每一列表示同一主题的一类文本,\(\Sigma\) 表示词语与文本间的相关性
李航老师的书中令 \(U_k\) 为 \(T\) 矩阵,\(\Sigma_k V_k^T\) 为 \(Y\) 矩阵
李航老师的书中并没给出令 \(U_k\) 为 \(T\) 矩阵,\(\Sigma_k V_k^T\) 为 \(Y\) 矩阵的原因,如果按照每个矩阵的含义猜测,或者说既然\(\Sigma\) 表示缩放量,那么其实也可以令 \(U_k \Sigma_k\) 为 \(T\) 矩阵,$ V_k^T$ 为 \(Y\) 矩阵,待验证~
如果只是单纯就最后的模型效果来看,直接将LSA理解为进阶版的SVD即可
1.2.2. 非负矩阵分解
SVD分解后的矩阵是有负值的,但非负矩阵可以看做是伪概率分布矩阵,其次,SVD的优化目标基于L-2 norm 或者 Frobenius Norm 的,这相当于隐含了对数据的高斯分布假设。而 term 出现的次数是非负的,这明显不符合 Gaussian 假设,而更接近 Multi-nomial 分布。
故,可以使用非负矩阵分解方法,更加具体地,给定非负矩阵 \(X \geq 0\) ,找到两个非负矩阵 \(W \geq 0\) 和 \(H \geq 0\) ,使得 \[ X \approx W H \] 其中,\(W\) 即 \(T\) 矩阵,也称基矩阵,\(H\) 即 \(Y\) 矩阵,也称系数矩阵
至于两个矩阵的求解可以看做是最优化问题求解
李航书中提供两种可参考的代价函数
1.2.2.1. 平方损失
\[ J(W,H) = \| X - WH \|^2 = \| A - B \|^2 =\sum_{i,j} (a_{ij}-b_{ij})^2 \]
该函数当且仅当 \(A=B\) 时,达到下界为0
对应的目标函数为 \[ \min_{W,H} \quad \| X - WH \|^2 \]
\[ s.t. \quad W,H \geq 0 \]
1.2.2.2. 散度
\[ J(W,H) = D(X\|WH) = D(A\|B) = \sum_{i,j} (a_{ij}\log\frac{a_{ij}}{b_{ij}}-a_{ij}+b_{ij}) \]
该函数当且仅当 \(A=B\) 时,达到下界为0
如果 \(\sum a_{ij} = \sum b_{ij} = 1\) 时,散度退化为 KL散度或相对熵
对应的目标函数为 \[ \min_{W,H} \quad D(X\|WH) \]
\[ s.t. \quad W,H \geq 0 \]
由于上诉两中代价函数都不是同时对两个变量的凸函数,所以只能通过数值计算求解。
以平方损失为例,采用梯度下降法进行求解
首先求每个变量对应的梯度 \[ \nabla_{W_{il}} = \frac{\partial J(W,H) }{\partial W_{il}} = -[(XH^T)_{il}-(WHH^T)_{il}] \\ 1\leq i \leq m,1 \leq l \leq k \]
\[ \nabla_{H_{lj}} = \frac{\partial J(W,H) }{\partial H_{lj}} = -[(W^TX)_{lj}-(W^TWH)_{lj}] \\ 1 \leq l \leq k, 1 \leq j \leq n \]
权值更新 \[ W_{il} \leftarrow W_{il} + \lambda_{il} \nabla_{W_{il}} \\ H_{lj} \leftarrow H_{lj} + \mu_{lj} \nabla_{H_{lj}} \] 传统的梯度下降算法对步长取一个常量,然后迭代值 \(W\) 和 \(H\) 收敛,算法结束
但这种方法收敛速度太慢,Lee和Seung基于”乘法更新规则“,对此继续进行优化
取 \[ \lambda_{il} = \frac{W_{il}}{(WHH^T)_{il}},\mu_{lj} = \frac{H_{lj}}{(W^TWH)_{lj}} \] 则可令权值的更新简化为 \[ W_{il} \leftarrow W_{il} \frac{(XH^T)_{il}}{(WHH^T)_{il}} \\ H_{lj} \leftarrow H_{lj} \frac{(W^TX)_{lj}}{(W^TWH)_{lj}} \] 只要选取初始矩阵 \(W\) 和 \(H\) 为非负的,即可保证迭代过程的矩阵 \(W\) 和 \(H\) 为非负的(书中没有直接给出该推断的证明过程,后面有时间再补吧)
2. references
《统计学习方法》17章,李航