机器学习神经网络生成模型

机器学习

发布日期: 2022-09-28

更新日期: 2024-01-28

文章字数: 6.2k

阅读时长: 25 分

阅读次数:

原始的GAN存在的很多问题，例如，没有给出具体的模型架构（主要是生成器），训练并不稳定等。后面提出的很多gan的改进模型都是围绕上面两个问题进行改进。

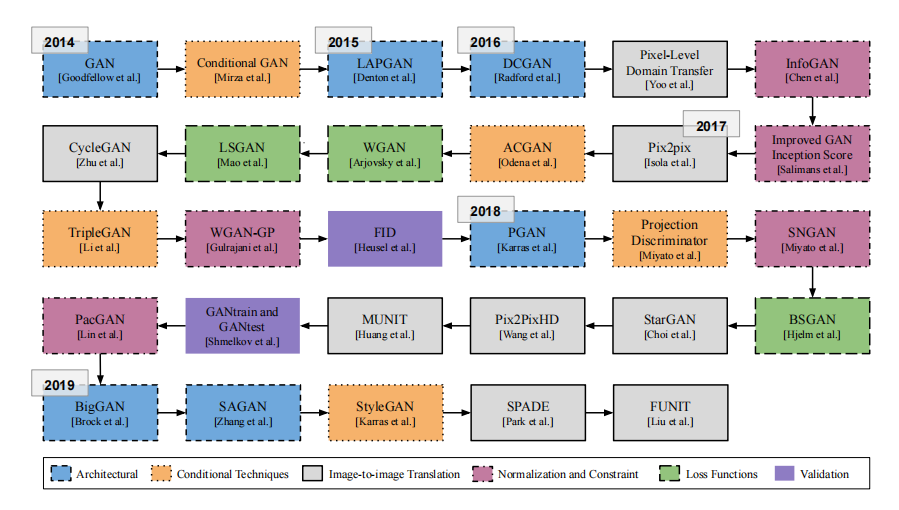
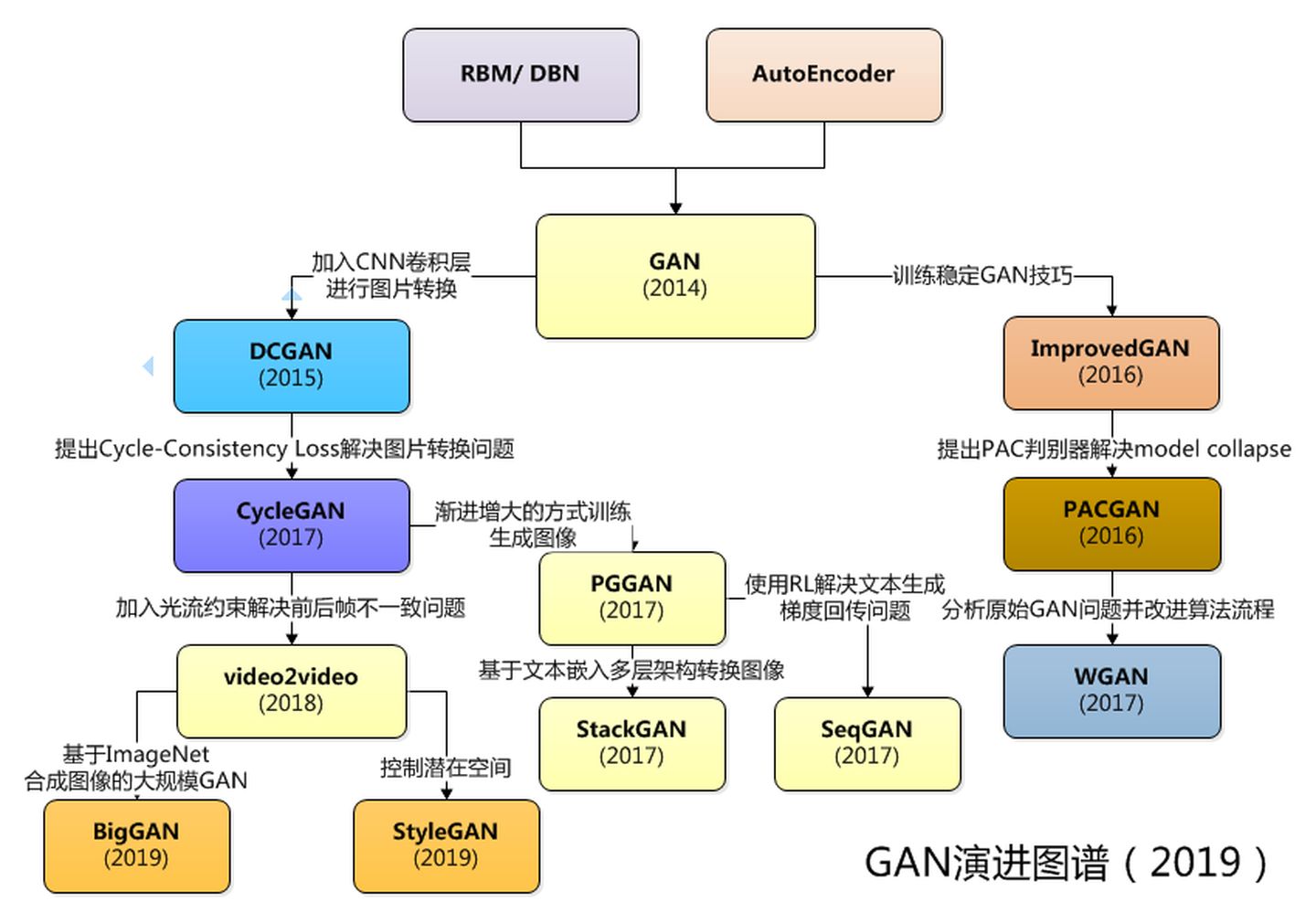
先给出两张GAN的演变史图片

这里还有一个收集了很多已提出的GAN网络的git仓库

下面挑一些个人认为比较典型突出的改进工作进行学习

1. CGAN

2014年的论文：Conditional Generative Adversarial Nets

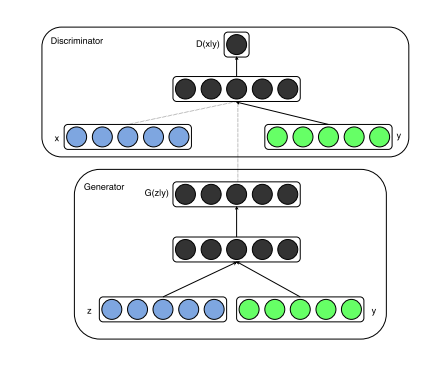
网络结构图

原始GAN的生成内容仅和生成器的参数和随机噪声有关，为了增强其结果的可控性，CGAN在判别器和生成器的输入中都加入一个条件变量 \(y\) ，这个条件变量通常是一些标签数据，所以该模型可以属于有监督的模型。

此时，生成器和判别器的输入分别变为 \(G(\boldsymbol{z} \mid \boldsymbol{y}))\) 和 \(D(\boldsymbol{x} \mid \boldsymbol{y})\)，模型的目标函数变为 \[ \min _G \max _D V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x} \mid \boldsymbol{y})]+\mathbb{E}_{\boldsymbol{z} \sim p_z(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z} \mid \boldsymbol{y})))] \]

2. DCGAN

2015年的论文：Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks

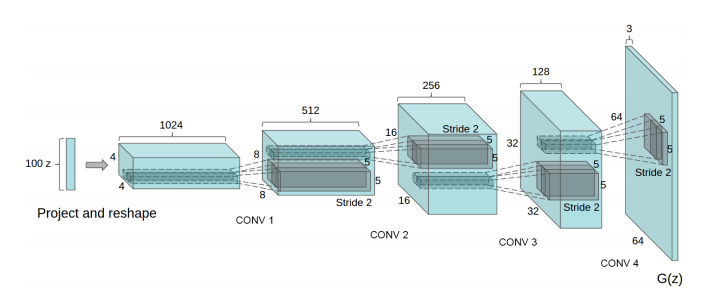
网络结构图

这篇论文最大的贡献就是提出了一个稳定通用的GAN基础架构，虽然现在看来，往模型中加入CNN网络，好像是很自然平常的事情，但在当时也是一件开创性的事件，因为其证明了GAN在图像生成任务上的可能性。

还有一些小的改进，这里也简单一提，包括，

取消池化层，判别器用带步长的卷积层代替，以及生成器用带分数步长（fractional-strided）代替；取消全连接层
生成器和判别器都采用batch norm
生成器除输出层使用tanh，其他层使用ReLU；判别器使用LeakyReLU

3. ImprovedGAN

NIPS 2016年的论文（Ian Goodfellow的续作）：Improved Techniques for Training GANs

官方代码：https://github.com/openai/improved-gan

论文中认为，仅靠梯度下降法，只能找到较低的损失点，但很难达到纳什均衡。所以论文提出了一些使收敛更加稳定的技巧

3.1. Feature matching

生成器优化过程中，从极大化 \(\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})} \mathbf{f}(G(\boldsymbol{z}))\) 改为极小化 \[ \left\|\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}} \mathbf{f}(\boldsymbol{x})-\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})} \mathbf{f}(G(\boldsymbol{z}))\right\|_2^2 \]

论文认为这样做可以使生成数据更加接近真实数据的分布，该思想可能来源于MMD距离。

最后，作者还提到，上式会有一个最优的固定点，使得生成数据和真实数据分布一致，但并不保证一定能找到，但确实有效（好像讲了什么，但好像又什么没讲，反正就是证明不了，但你尽管用就是了）

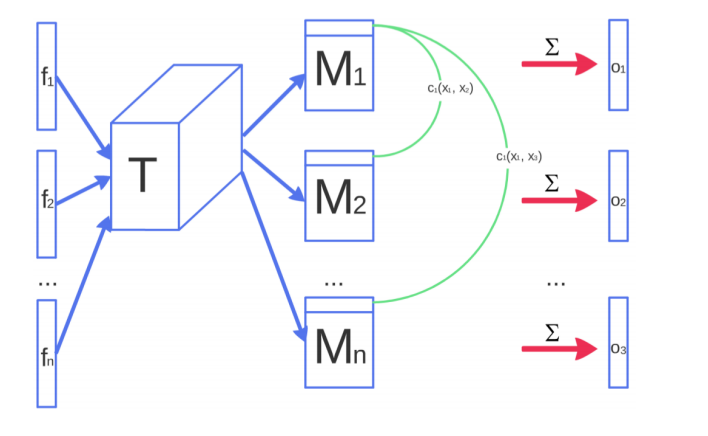
3.2. Minibatch discrimination

GAN模型中存在名为模式坍塌（mode collapse）的问题，即生成器生成的图像虽然很像真实图像，但非常单一，来来去去都只有一两张图片。

为了缓解这个问题，论文中将判别器中单个样本输入，改为一个batch输入。但与传统的Minibatch不一样，论文中对每个batch中样本做了一些融合处理。具体步骤如下：

每个batch有 \(n\) 个样本，样本 \(x_i\) 对应的向量为 \(f(x_i) \in \mathbb{R}^A\)
将 \(f(x_i)\) 与一个张量 \(T \in \mathbb{R} ^{A \times B \times C}\) 相乘，得到张量 \(M_i \in \mathbb{R}^{B \times C}\)
对 \(M\) 的每一个样本对应行两两求L1距离，得 \(c_b\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right)=\exp \left(-\left\|M_{i, b}-M_{j, b}\right\|_{L_1}\right) \in \mathbb{R}\)
求和，得 \(o\left(\boldsymbol{x}_i\right)_b =\sum_{j=1}^n c_b\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right) \in \mathbb{R}\)
拼接，得 \(o\left(\boldsymbol{x}_i\right) =\left[o\left(\boldsymbol{x}_i\right)_1, o\left(\boldsymbol{x}_i\right)_2, \ldots, o\left(\boldsymbol{x}_i\right)_B\right] \in \mathbb{R}^B\)
最终有 \(o(\mathbf{X}) \in \mathbb{R}^{n \times B}\)

结构图如下

3.3. Historical averaging

生成器和判别器的目标函数中均加入一个正则项 \[ \left\|\boldsymbol{\theta}-\frac{1}{t} \sum_{i=1}^t \boldsymbol{\theta}[i]\right\|^2 \]

该正则项常应用在在线学习中。

这个正则项的特点是一个与迭代次数相关的函数，模型参数可以在长时间内受到尺度约束，作者希望模型在学习新的样本数据时不要忘记之前样本学习的经验

3.4. One-sided label smoothing

通过

\[ D(\boldsymbol{x})=\frac{\alpha p_{\text {data }}(\boldsymbol{x})+\beta p_{\text {model }}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_{\text {model }}(\boldsymbol{x})} \]

对判别器中真实样本输出乘 \(\alpha\) ，生成样本输出乘 \(\beta\)，即将 \(\{0, 1\}\) 硬标签转化为 \([\beta,\alpha]\) 的软标签，使模型训练更加soft，属于分类器训练常用的trick了

3.5. Virtual batch normalization

论文认为梯度下降非常依赖每个batch的样本分布，而一个batch的分布可能并不能反映整体的分布。

为了缓解这个问题，论文在开始训练前，挑选一组固定的参考样本（reference batch），将其与每个batch耦合后，再计算均值和标准差，将分布拉回原始数据分布。有点类似于残差结构的思想。

但这个方法计算成本太高，所以论文只在生成器中运用。

3.6. Semi-supervised learning

原始GAN是无监督的，其判别器是一个一维向量，只能判别样本是否为真。

论文对其扩展至 \(K + 1\) 维向量，使其可以应用于部分打标样本的半监督场景。其中，已打标的样本对应一个 \(K\) 类的分类任务；而未打标的样本对应最后 \(1\) 维正例样本，生成器输出的样本对应其负例样本。

损失函数如下 \[ \begin{aligned} \mathcal{L} &=-\mathbb{E}_{\boldsymbol{x}, y \sim p_{\text {data }}(\boldsymbol{x}, y)}\left[\log p_{\text {model }}(y \mid \boldsymbol{x})\right]-\mathbb{E}_{\boldsymbol{x} \sim G}\left[\log p_{\text {model }}(y=K+1 \mid \boldsymbol{x})\right] \\ &=\mathcal{L}_{\text {supervised }}+\mathcal{L}_{\text {unsupervised }} \\ \mathcal{L}_{\text {supervised }} &=-\mathbb{E}_{\boldsymbol{x}, y \sim p_{\text {data }}(\boldsymbol{x}, y)} \log p_{\text {model }}(y \mid \boldsymbol{x}, y<K+1) \\ \mathcal{L}_{\text {unsupervised }} &=-\left\{\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})} \log \left[1-p_{\text {model }}(y=K+1 \mid \boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{x} \sim G} \log \left[p_{\text {model }}(y=K+1 \mid \boldsymbol{x})\right]\right\} \end{aligned} \] 令 \(D(\boldsymbol{x})=1-p_{\text {model }}(y=K+1 \mid \boldsymbol{x})\)，\(L_{\text {unsupervised }}\) 就是原始GAN判别器的损失函数了

4. WGAN

2017年的论文：

参考文章：https://zhuanlan.zhihu.com/p/25071913

代码实现：

官方基于pytorch的实现代码
个人基于pytorch的实现代码

作者用了两篇论文来介绍WGAN，其中第一篇主要分析原始GAN的问题，第二篇才正式推出GAN

4.1. 随机噪声

这是第一篇论文给出的一个解决方案

作者认为，在通常情况下，高维空间中自然分布的两个曲面（真实样本和生成样本就可以看作是这样的两个曲面）不重叠或重叠可忽略（即不相关？）的概率很大，所以一定存在一个曲面将其分隔开，考虑到神经网络超强的拟合能力，随着训练的迭代，必然会得到一个训练很好的判别器。

当判别器为最优判别器时，此时生成器的损失函数可以看做是一个简单的 \(J S D\left(\mathbb{P}_{r} \| \mathbb{P}_{g}\right)\) 。而当两个分布不重叠或重叠可忽略时，JS函数的梯度趋近于0。所以当判别器训练得越好时，生成器就越难继续往下迭代。

对此，作者分别向真实样本和生成样本中添加随机噪声，其分布分别为 \(\mathbb{P}_{r+\epsilon}\) 和 \(\mathbb{P}_{g+\epsilon}\)。这样做可以使两个分布产生一些不可忽略的重叠，一方面使其更难找到最优的判别器，另一方面由于重叠不可忽略，所以生成器的反向梯度也不为0

添加噪声后的损失函数变为 \[ W\left(\mathbb{P}_r, \mathbb{P}_g\right) \leq 2 V^{\frac{1}{2}}+2 C \sqrt{J S D\left(\mathbb{P}_{r+\epsilon} \| \mathbb{P}_{g+\epsilon}\right)} \\ where \quad V=\mathbb{E}\left[\|\epsilon\|_2^2\right] \]

4.2. Wasserstein距离

Wasserstein距离又叫Earth-Mover（EM，推土机）距离，其原始表达式如下

\[ W\left(\mathbb{P}_r, \mathbb{P}_g\right)=\inf _{\gamma \in \Pi\left(\mathbb{P}_r, \mathbb{P}_g\right)} \mathbb{E}_{(x, y) \sim \gamma}[\|x-y\|] \] 其中，

\(\Pi\left(\mathbb{P}_r, \mathbb{P}_g\right)\) 表示随机分布 \(\mathbb{P}_r\) 和 \(\mathbb{P}_g\) 组合起来的所有可能的联合分布的集合
\(\inf\) 表示函数的下界
x，y在这里分别表示真实样本和生成样本

上式的含义是，遍历所有的 \(\gamma \in \Pi\left(\mathbb{P}_r, \mathbb{P}_g\right)\) ，通过采样 \((x, y) \sim \gamma\) ，计算xy距离 \(\|x-y\|\) 的期望，最后求取所有的 \(\gamma\) 对应的期望的最小值

Wasserstein距离对比JS距离或者KL距离，一个很重要的特性是，当两个分布没有重叠时，JS距离或者KL距离是一个不可微的分段常量函数，而Wasserstein距离大概率仍是一个可微的平滑函数。

又通常情况下，真实样本分布和生成样本分布不重叠或重叠可忽略的概率很大，所以基于JS散度的损失函数很容易发散。

但由于 \(\inf _{\gamma \in \Pi\left(\mathbb{P}_r, \mathbb{P}_g\right)}\) 无法直接求导，所以论文对其进行了如下变换 \[ W\left(\mathbb{P}_r, \mathbb{P}_\theta\right)=\sup _{\|f\|_L \leq K} \mathbb{E}_{x \sim \mathbb{P}_r}[f(x)]-\mathbb{E}_{x \sim \mathbb{P}_\theta}[f(x)] \]

其中，

\(\|f\|_L\) 表示函数 f 的Lipschitz常数
\(\sup\) 表示函数的上界

引入超参数 \(w\) 替换，用weight clipping来使 \(f_w\) 满足Lipschitz，上式进一步改造为 \[ K W\left(\mathbb{P}_r, \mathbb{P}_\theta\right) \approx \max _{w \in \mathcal{W}} \mathbb{E}_{x \sim \mathbb{P}_r}\left[f_w(x)\right]-\mathbb{E}_{z \sim p(z)}\left[f_wg_\theta(z)\right] \] 只保留右侧表达式，即可得WGAN的损失函数 \[ \mathcal{L} = \mathbb{E}_{x \sim \mathbb{P}_r} \left[f_w(x)\right]-\mathbb{E}_{z \sim p(z)}\left[f_wg_\theta(z)\right] \] 其中，

生成器的损失函数为 \(-\mathbb{E}_{z \sim p(z)}\left[f_wg_\theta(z)\right]\)
判别器的损失函数为 \(\mathbb{E}_{z \sim p(z)}\left[f_wg_\theta(z)\right] - \mathbb{E}_{x \sim \mathbb{P}_r} \left[f_w(x)\right]\)

可以发现，其最终形式很简单，就是比原始GAN少了log计算

注，上面详细推导见论文的附录

作者认为原始GAN的损失函数的值无法作为模型效果的指标，而WGAN的损失函数的值可以作为模型效果的指标。

最终参数更新过程如下

注：作者还认为，基于动量的优化算法给出的更新方向容易与梯度方向的夹角的cos值变成负数，导致迭代不稳定，所以尽量不要使用基于动量的优化算法（如Adam）或者使用很高的学习率

最后，作者还通过实验说明，WGAN并没有出现模式坍塌的问题

在这篇博客WGAN的成功，可能跟Wasserstein距离没啥关系中，作者对“WGAN的成功归功于Wasserstein距离”这一观点产生了质疑

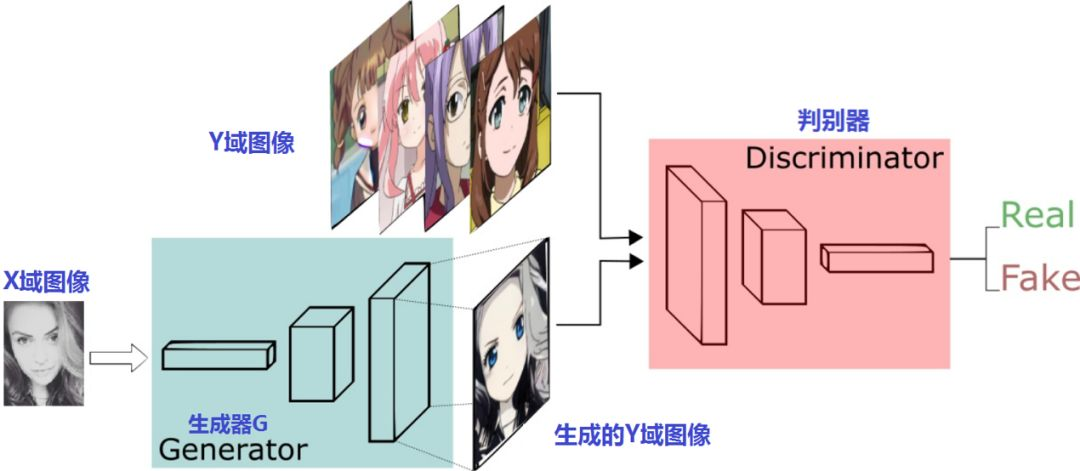
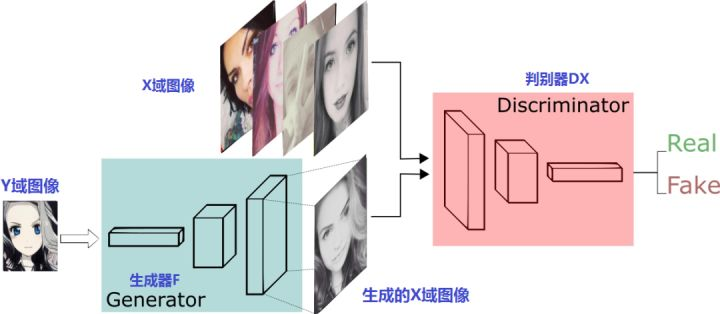
5. Pix2pix

2017年的论文：Image-to-Image Translation with Conditional Adversarial Networks

代码实现：

官方基于pytorch的实现代码
官方基于pytorch的实现代码

模型结构

这篇论文最大的贡献是提出了一个统一的框架解决了图像翻译问题（输入一张图片，输出另外一张相关的图片，例如风格迁移就是其中一类典型的图像翻译任务）

5.1. CGAN

Pix2pix是基于CGAN的改进，其训练需要一组两张翻译前后的图片。

生成器输入为翻译前的样本 \(x\) 和噪声 \(z\) （上面的结构图中省去噪声 \(z\) ，是因为在实际实验中，噪声往往被淹没在条件当中，所以就直接省去了）；判别器的输入为翻译前的样本 \(x\) 和生成器输出 \(G(x)\) / 翻译后的样本 \(y\)

Pix2pix的损失函数就是在CGAN的基础上加入一个正则项，即 \[ \begin{aligned} \mathcal{L} &= \mathcal{L}_{cGAN} + \mathcal{L}_1 \\ &= \mathbb{E}_{\boldsymbol{x} ,\boldsymbol{y}}[\log D(\boldsymbol{x} ,\boldsymbol{y})]+\mathbb{E}_{\boldsymbol{x} ,\boldsymbol{z}}[\log (1-D(G(\boldsymbol{x} , \boldsymbol{z})))] + \mathbb{E}_{(\boldsymbol{x} ,\boldsymbol{y},\boldsymbol{z})}[\|\boldsymbol{y} - G(\boldsymbol{x},\boldsymbol{z})\|] \end{aligned} \]

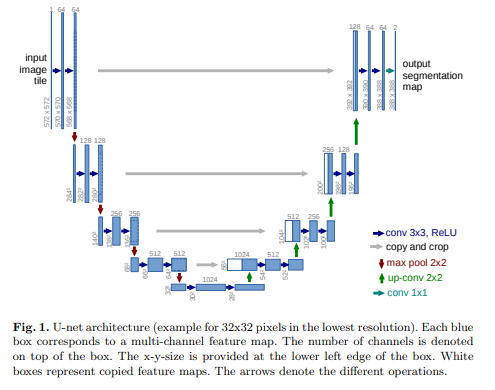
5.2. U-net

来自2015的论文：U-Net: Convolutional Networks for Biomedical Image Segmentation

模型结构：

这是一个和FPN很像的结构，两者的差异：

FPN用于图像检测，U-net用于图像分割
FPN有多个预测输出，U-net只有一个
FPN的特征图融合是直接相加，U-net是沿通道方向直接拼接在一起

论文将U-net应用到了模型的生成器中

5.3. PatchGAN

论文认为判别器输入的图像的分辨率太高，导致判别器太弱，以至于无法生成清晰的图片。

所以论文将判别器的输入图像分成 N×N 个图像块（Patch），然后再分批进行预测，最后将所有Patch的Loss求平均作为最终的Loss

论文称这种方法为PatchGAN（如果分成的图像块是1×1 的像素点，则称其为PixelGAN；如果之分成1个图像块，则称其为ImageGAN）

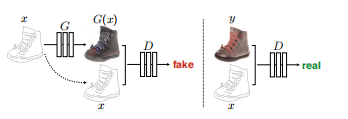
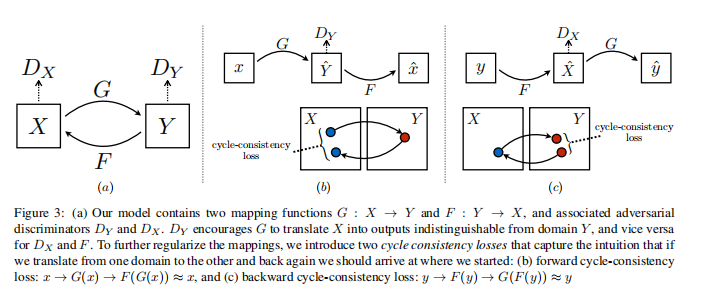
6. CycleGAN

2017年ICCV的论文：Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks

代码实现：

官方基于pytorch的实现代码
个人基于pytorch的实现代码

模型结构

这篇论文同样是用于图像翻译任务，其最大的亮点是，不要求训练样本要成对出现，即提供一种通过无监督学习（准确来说是半监督学习？因为还是需要预先将样本分成两部分）来解决图像翻译任务的方法。

将\(X\)转换成\(Y\)后，再将\(Y\)转换成 \(\hat X\)，如果 \(X=\hat X\)，则称其为具有循环一致性（cycle consistency）的特性

根据这一想法，如下图所示

论文设计了两个生成器 \(G\) 和 \(F\)，分别负责将将\(X\)转换成\(Y\)和将\(Y\)转换成 \(X\)；对应的也有两个判别器，其输出分别为 \(D_X=D(F(y))\) 和 \(D_Y=D(G(x))\)

设计思路看上去还是很简单，就是将一个原始GAN网络复制两份，然后将两个GAN生成器的两个输入相互调换，对称式训练，最后再将两部分联合求解即可。但实际上，由于网络交错复杂，还是很容易把人绕晕的

生成器模型的损失函数为 \[ \begin{aligned} \mathcal{L}\left(G, F, D_X, D_Y\right) =&\mathcal{L}_{\mathrm{GAN}}\left(G, D_Y, X, Y\right) +\mathcal{L}_{\mathrm{GAN}}\left(F, D_X, Y, X\right) +\lambda \mathcal{L}_{\mathrm{cyc}}(G, F) \\ \mathcal{L}_{\mathrm{GAN}}\left(G, D_Y, X, Y\right) = & \mathbb{E}_{y \sim p_{\text {data }}(y)}\left[\log D_Y(y)\right]+\mathbb{E}_{x \sim p_{\text {data }}(x)}\left[\log \left(1-D_Y(G(x))\right)\right] \\ \mathcal{L}_{\mathrm{GAN}}\left(F, D_X, Y, X\right) = & \mathbb{E}_{x \sim p_{\text {data }}(x)}\left[\log D_X(x)\right]+\mathbb{E}_{y \sim p_{\text {data }}(y)}\left[\log \left(1-D_X(F(y))\right)\right] \\ \mathcal{L}_{\mathrm{cyc}}(G, F) = & \mathbb{E}_{x \sim p_{\text {data }}(x)}\left[\|F(G(x))-x\|_1\right] + \mathbb{E}_{y \sim p_{\text {data }}(y)}\left[\|G(F(y))-y\|_1\right] \end{aligned} \] 其中，\(\mathcal{L}_{\mathrm{cyc}}\) 为正则项

上面 \(\mathcal{L}_{\mathrm{GAN}}\) 论文中第一项给出的是 \(\mathbb{E}_{y \sim p_{\text {data }}(y)}\left[\log D_Y(y)\right]\)，但阅读官方的源码时发现，使用的是 \(\mathbb{E}_{y \sim p_{\text {data }}(y)}\left[\|\|G(y)-y\|_1\right]\)

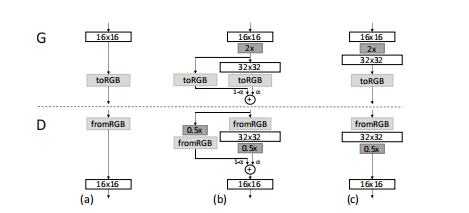
7. PGGAN（ProGAN）

ICLR 2018年的论文：Progressive Growing of GANs for Improved Quality, Stability, and Variation

官方代码：https://github.com/tkarras/progressive_growing_of_gans

该论文主要提供了一个生成高分辨率图像的解决方案

7.1. progressive train

论文认为，既然很难一次性生成高质量的高分辨率图片，那么可以由浅入深，先训练可以生成高质量的低分辨率的图片的GAN。训练完成后，在此基础上，添加一些网络中间层，加深网络，然后训练可以生成更高分辨率的GAN。按此一步步的训练出可以生成高质量的高分辨图片的GAN

但直接添加层，会使得模型训练不稳定，所以论文提出一种如下渐进式的增加网络深度的结构

其中，\(\alpha \in [0,1]\) 是权重因子，初始化为0，表示该层不存在，然后随迭代次数增加，直到增大到为1，表示该层被完全添加到网络中。

7.2. Minibatch standard deviation

在ImprovedGAN中，为了增加生成样本的多样性，提出了Minibatch discrimination的技巧，但PGGAN认为这太复杂了，所以直接简化为Minibatch standard deviation操作。其做法很简单，就是对每个minibatch的样本计算每一个特征（即沿通道方向计算）的标准差和方差，得到一个和特征图同样大小的矩阵，然后直接拼接，作为特征图的一个通道进行输出

7.3. equalized learning rate

通过 \(w_i = w_i /c\) 动态控制网络的权重，其中 \(c\) 为何凯明初始化常数（He’s initializer）

7.4. pixel-normalization

为了防止生成器和判别器恶性竞争，导致系统失控，在生成器的每个卷积操作后，添加如下的pixel-normalization操作 \[ b_{x, y}=\frac{a_{x, y}} {\sqrt{\frac{1}{N} \sum_{j=0}^{N-1}\left(a_{x, y}^j\right)^2+\epsilon} } \]

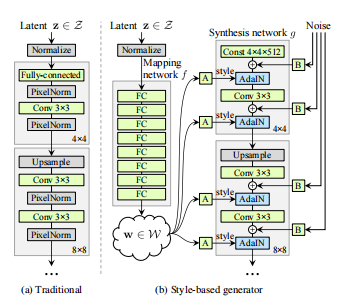
8. StyleGAN

2019年的论文：A Style-Based Generator Architecture for Generative Adversarial Networks

代码实现：

官方基于pytorch的实现代码
个人基于pytorch的实现代码

生成器网络结构图

PGGAN作者的另一作品，StyleGAN也套用了PGGAN渐进式的训练策略。

该论文最大的贡献是，提出了噪声可以从生成器的任意中间层中加入，强化并细化了噪声对网络的影响，从而更好的控制图片的一些细节部分的生成

注：个人认为这种方式其实和CGAN很很像，就是把噪声当成条件进行输入。

8.1. Mapping Network

论文认为每一种风格（style）都可以由隐空间中一维向量决定，所以如果可以将隐空间进行解纠缠（disentangled），得到特定风格的控制变量表示，就可以生成具有对应风格特征的图片。

论文通过名为映射网络（Mapping Network，即一系列的全连接层）的结构，将原始的隐变量 \(z\) 映射为控制变量 \(w\)

8.2. AdaIN

论文通过一个名为自适应实例规范化（adaptive instance normalization，AdaIN）的模块，将控制变量 \(w\) 和每个生成器中间层的输出 \(x\) 进行耦合

在耦合前，还需要将 \(w\) 变换成风格 \(y= (y_s,y_b)\) （论文并没有给出 \(w\) 转换成 \(y\) 的方式，结合网上相关的资料，猜测是添加一层全连接层），然后进行如下计算 \[ \operatorname{AdaIN}\left(\mathbf{x}_i, \mathbf{y}\right)=\mathbf{y}_{s, i} \frac{\mathbf{x}_i-\mu\left(\mathbf{x}_i\right)}{\sigma\left(\mathbf{x}_i\right)}+\mathbf{y}_{b, i} \] 上式原理很简单，就是对 \(x\) 标准化后，进行一次线性变换。

8.3. Const input

论文认为，既然生成器每个中间层的输入都会受 \(A\) 的影响，生成器的输入其实已经无关重要了，所以使用一个固定常量作为输入即可

8.4. Random noise

论文还在每个中间层的输出与一个随机的噪声 \(B\) 进行相加，用来控制一些随机的微小特征的生成，使生成的图片更加多变及真实。

9. SAGAN

2018年的论文：Self-Attention Generative Adversarial Networks

官方代码：https://github.com/brain-research/self-attention-gan

9.1. Non-local Neural Networks

SAGAN生成器使用的是论文Non-local Neural Networks中提出的结构，这是一个attention+残差的模块

首先输入接入一个典型的attention结构

对应的表达式 \[ v(x) = \text{Attention}(f(x),g(x),h(x)) = \text{softmax}\left(f(x)g(x)^{\top}\right)h(x) \\ h(x) = W_h x \\ f(x) = W_f x \\ g(x) = W_g x \\ \] 然后再接上一个残差结构，便是Non-local Neural Networks的输出了 \[ y = \gamma (W_v v(x)) + x \]

9.2. hinge损失

损失函数采用hinge损失，这算是一个创新点 \[ \begin{aligned} L_D & =-\mathbb{E}_{(x, y) \sim p_{\text {data }}}[\min (0,-1+D(x, y))]-\mathbb{E}_{z \sim p_z, y \sim p_{\text {data }}}[\min (0,-1-D(G(z), y))] \\ L_G & =-\mathbb{E}_{z \sim p_z, y \sim p_{\text {data }}} D(G(z), y) \end{aligned} \]

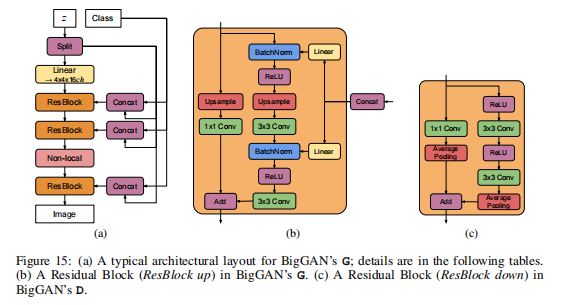
10. BigGAN

DeepMind 2019年的论文：Large Scale GAN Training for High Fidelity Natural Image Synthesis

10.1. large model

BigGAN在SAGAN的基础上，通过实验发现，增大batch size的大小（最终增大至2048）、增大生成器中间层的通道数（最终比原来增大了50%）以及增加网络深度（最终网络参数达16亿），可以显著提升模型的效果。一言蔽之，大力出奇迹。

除了加大网络参数，还参考了ProGAN，加入一个类别条件参数，并且该参数可以在生成器的任意中间层中加入，使其可以生成指定类别的图像

下面贴出来的是基础BigGAN结构图，论文中还有BigGAN-deep的结构图，这里就不一一贴出来了

10.2. truncation trick

论文认为噪声不一定只能是标准正态分布或者均匀分布，所以采用一种名为截断技巧（truncation trick，即设定一个阈值，当采样数据大于该阈值时，则重新采样）的处理手段，对标准正态分布进行截断采样。

通过实验，论文发现随着截断阈值的下降，图像的质量会逐渐提高，图像的多样性会逐渐下降。这个结果是符合主观猜测的。

论文还发现，一些大型的模型采用截断技巧后，会出现饱和伪影（saturation artifacts）的现象。论文认为这是因为噪声 \(z\) 没有投影到整个样本空间，所以加入了如下正则项，使噪声强制与样本正交，以投影到整个样本空间 \[ R_\beta(W)=\beta\left\|W^{\top} W \odot(\mathbf{1}-I)\right\|_{\mathrm{F}}^2 \]

10.3. characterizing instability

论文还发现了有一些层在训练过程中会出现参数爆炸的情况，通过对生成器参数更新范围的限制（具体公式请查看原论文），实验结果分析认为，这一种现象是无法避免的；通过对判别器添加不同的正则项（具体正则项请查看原论文），实验结果分析认为，对判别器的惩罚力度越大，模型的性能越稳定，但训练成本也越高，且图像生成质量也越差。

另外，论文中还介绍了很多调参的技巧，这里就不展开介绍了。