生成对抗网络(Generative Adversarial Networks,GAN)是一个通过对抗的方式,去学习数据分布的生成式模型
一些题外话:
据说当年GAN的提出者Ian Goodfellow,在NIPS大会讲解GAN的时候,遭到 Jürgen Schmidhube (RNN网络的提出者)的质疑,称其疑似抄袭自己的论文,当然Goodfellow也解释了之前已经和Schmidhube通了好几次邮件,详细分析了两个算法的异同之处,否认了抄袭。
这就当两个深度学习界的大佬间的一个趣谈了。
1. 输入输出
训练输入: \[ X= \{x_1, x_2, ..., x_N\} \\ Z=\{z_1,z_2,...,z_{N}\} \] 其中,
- \(x_i \in \mathbb{R}^{m},i =1,2,...,N\),\(x_i\) 为特征域
- \(z_i \in \mathbb{R}^k,,i =1,2,...,N\),\(z_i\) 为噪声域
测试输入 \[ Z'=\{z'_1,z'_2,...,z'_{N'}\},z'_i \in \mathbb{R}^k \] 测试输出: \[ \hat X'=\{\hat x'_1, \hat x'_2,..., \hat x'_{N'}\},\hat x'_i \in \mathbb{R}^m \]
2. 基本定义
2.1. 模型推导
GAN的结构和VAE是很像的,也是分为两部分:生成器G(Generator)和判别器D(Discrimnator)。
顾名思义,生成器的作用是通过给定的噪声 \(z \sim p_{Z}\) 生成样本 \(\hat x\) ;判别器的作用的区分生成数据 \(\hat x\) 和真实数据 \(x \sim p_{data}\) 。常见的通俗理解是,将生成器当作是一个造假者,将判别器当作是一个鉴别者。造假者努力提升自己,制造赝品,欺骗鉴别者;而鉴别者也努力提升自己,区分出赝品。在造假和鉴假的过程中,两者相互学习,相互提高,即所谓的“魔高一尺,道高一丈”的对抗式学习。
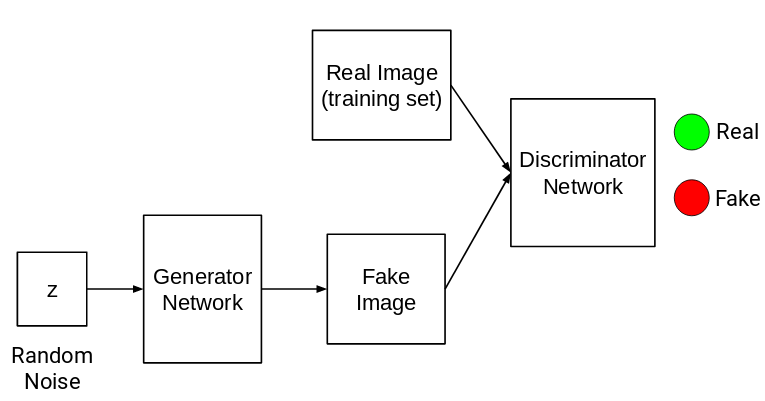
GAN的整体结构如下所示
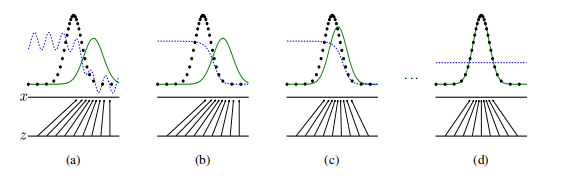
理想情况下的数据分布变化如下图所示
上图中,
- 黑色虚线表示真实的样本的分布情况,蓝色虚线表示判别器判别概率的分布情况,绿色实线表示生成样本的分布。\(Z \rightarrow x\) 表示从噪声生成数据的过程。
- a图表示系统的初始状态,由于并未经过训练,生成器的生成分布和真实分布区别很大,判别器对两者的预测不稳定。
- b图表示只对判别器训练,此时判别器的效果很好。
- c图表示同时对判别器和生成器训练,此时生成器的生成分布逐渐拟合真实分布,判别器的效果逐渐下降。
- d图表示系统的最终状态,此时生成器的生成分布和真实分布基本一致,判别器无法分辨样本是生成的还是真实的(\(D(x) = 1/2\))。
2.2. 学习策略
这里只考虑一般情况下的推导,所以不讨论 \(D(x;\theta_d)\) 、 \(G(z;\theta_g)\) 及 \(z\) 的具体表达形式。
下面直接给出模型的目标函数
\[ \min _G \max _D V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))] \]
注:
VAE和GAN一个很大的区别是目标函数的关注点不一样,对比VAE的目标函数显式地包含了对噪声的计算,GAN的目标函数只显式的包含了对最终结果的计算。
另外,有一种观点认为,VAE是pointwise的,所以会脱离数据流形面,因此看起来生成的图片会比较模糊
上式中,
- 从构成要素来看,\(\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]\) 表示判别器D对真实数据的区分能力;\(\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]\) 表示判别器D对生成数据的区分能力,由于我们希望判别器最终无法区分生成数据,所以这里用的是 \(1-D\) ,这也和前一部分形成了对抗之势。
- 从解决目标来看,\(\max_D\) 表示固定生成器G,求解最优的判别器D;\(\min_G\) 表示固定判别器D,求解最优的生成器G。求解的顺序可以调换,但先max再min的推导会更加方便。
下面对上式进行进一步的推导
对 \(V(G, D)\) 进一步展开 \[ \begin{aligned} V(G, D) &=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x})) d x+\int_z p_{\boldsymbol{z}}(\boldsymbol{z}) \log (1-D(g(\boldsymbol{z}))) d z \\ &=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x}))+p_g(\boldsymbol{x}) \log (1-D(\boldsymbol{x})) d x \end{aligned} \] 由于 \(D(x)\) 为一般形态,所以将 \(x\) 当作常量,令 \[ f(D) = p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x}))+p_g(\boldsymbol{x}) \log (1-D(\boldsymbol{x})) \] 求解 \(\arg \max_D V(D,G)\) 可以转化为 \(\arg \max_D f(D)\),即 \[ D^* = \arg \max_D f(D) \] 得 \[ D_G^*(\boldsymbol{x})=\frac{p_{\text {data }}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x})} \] 代入 \(V(G,D)\) 中,有 \[ \begin{aligned} C(G) &=\max _D V(G, D) = V(G, D^*) \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_G^*(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}\left[\log \left(1-D_G^*(G(\boldsymbol{z}))\right)\right] \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_G^*(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{x} \sim p_g}\left[\log \left(1-D_G^*(\boldsymbol{x})\right)\right] \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{p_{\text {data }}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x})}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_g}\left[\log (1- \frac{p_\text {data }(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x})})\right] \end{aligned} \]
得生成器的目标函数 \[ \begin{aligned} C(G) &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{p_{\text {data }}(\boldsymbol{x})}{P_{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x})}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_g}\left[\log \frac{p_g(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x})}\right] \\ &= \mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{p_{\text {data }}(\boldsymbol{x})}{ (P_{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x}))/2}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_g}\left[\log \frac{p_g(\boldsymbol{x})}{(p_{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x}))/2}\right] - 2\log2 \\ &= -\log 4+K L\left(p_{\text {data }} \| \frac{p_{\text {data }}+p_g}{2}\right)+K L\left(p_g \| \frac{p_{\text {data }}+p_g}{2}\right) \end{aligned} \]
吐槽一下,原论文这里的推导很乱,让人看得云里雾里得。上面的推导过程和原论文中的推导不一样
上式的除2操作是为了更方便的将KS散度转换为JS散度,整理得最终的目标函数为 \[ G^* = \arg \min_G C(G) = JSD(p_{\text{data} } || p_g) \\ 0 \leq JSD(p_{\text{data} } || p_g) \leq \log2 \]
注:
JS散度( Jensen–Shannon divergence,JSD)是一个对称的函数,与KS散度的关系为 \[ J S D(P \| Q)=\frac{1}{2} K L(P \| M)+\frac{1}{2} K L(Q \| M) \\ M = \frac{1}{2}(P + Q) \]
2.3. 学习算法
上面看似推导了很多,但实际上只是理想情况下模型的表示形式,而且难以优化(就是经典的图一乐的推导)。对于一般情况下,还是使用梯度法(一般就是神经网络了)对原式(非JS距离形式的目标函数)进行求解。
由于实际样本是有限的,所以只能求解近似解。
从 \(p_{data}\) 和 \(p_Z\) 中分别采样 \[ X= \{x_1, x_2, ..., x_N\} \\ Z=\{z_1,z_2,...,z_{N}\} \] 将期望计算转为近似计算,得 \[ V(D,G) = \frac{1}{N} \sum_{i=1}^N\left[\log D\left(\boldsymbol{x}_i\right)+\log \left(1-D\left(G\left(\boldsymbol{z}_i\right)\right)\right)\right] \] 参数更新分成两个部分
首先,优化判别器,即使用梯度上升法求解 \(\max_D\) ,参数更新表达式 \[ \theta_d \leftarrow \theta_d + \eta \nabla_{\theta_d} V \] 这一步骤通常重复若干次
接着,优化生成器,即使用梯度下降法求解 \(\min_G\) ,参数更新表达式 \[ \theta_g \leftarrow \theta_g - \eta \nabla_{\theta_g} V \] 由于第一项不涉及 \(\theta_g\) ,所以 \(\nabla_{\theta_g} V\) 可以简写为 \[ \nabla_{\theta_g} = \frac{1}{N} \sum_{i=1}^N\log \left(1-D\left(G\left(\boldsymbol{z}_i\right)\right)\right) \] 这一步骤通常只重复一次
两个部分交替进行,直到模型完全收敛(纳什均衡(Nash equilibrium))。
注:
之所以判别器更新多次后,生成器才更新一次,一种观点认为生成器的效果更依赖判别器的效果。判别器太弱,生成器容易停滞不前;判别器太强,生成器难以学习到知识。WGAN对此也给出了详细的数学推导证明,当然这是后话了。
最后,判别器更新次数的设置是需要有一定的先验知识的,在先验知识比较匮乏的时候,一般设置判别器更新次数为1,然后看效果再慢慢增大判别器更新次数。
整体流程的伪代码如下
3. references
Generative Adversarial Networks