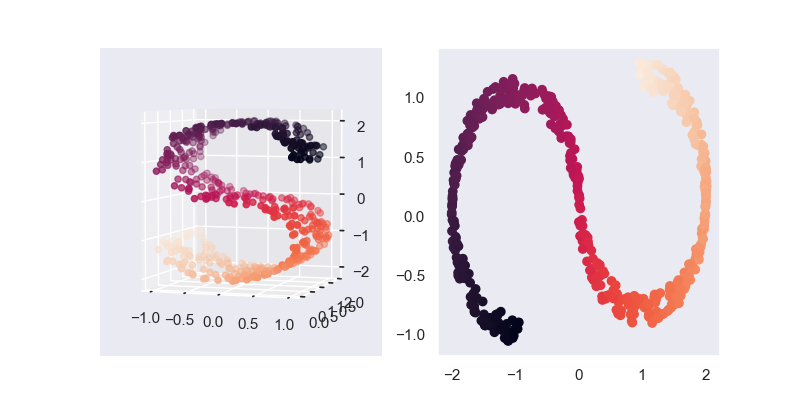
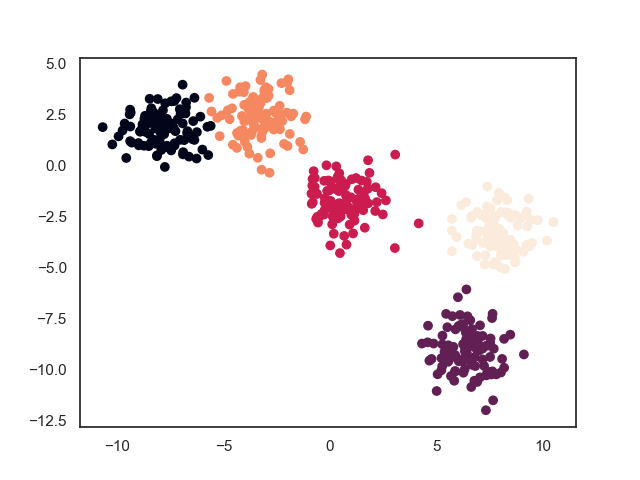
基于numpy的实现代码传送门
奇异值分解(Singular Value Decomposition,SVD)是一种线性代数工具,机器学习中常被用于数据降维任务。
1. 降维定义
数据在降维前,不同维度的特征不一定完全正交,所以会存在信息冗余的部分。而降维算法对通过将高维空间投射到低维空间中,只保留数据相互正交的信息,达到对数据压缩的目的。
降维后的矩阵的信息一定是会损失的。评价一个降维算法的优劣不是一件容易的事情,一般以
- 最小信息损失率
- 最大数据压缩率
作为评价的指标.
降维算法的流程一般都比较简单,可以看做是一种简单的数学工具,但由于在机器学习中应用广泛,加上推导过程一般都比较繁琐,所以也将其归为一种算法,如果没有特殊说明,一般将其归为无监督学习的一种。
2. 输入输出
Input:
原始矩阵 \[ A = [a_{ij}]_{m \times n} \] Output:
降维后的矩阵 \[ A' = [a'_{ij}]_{m \times n} \]
3. 模型效果
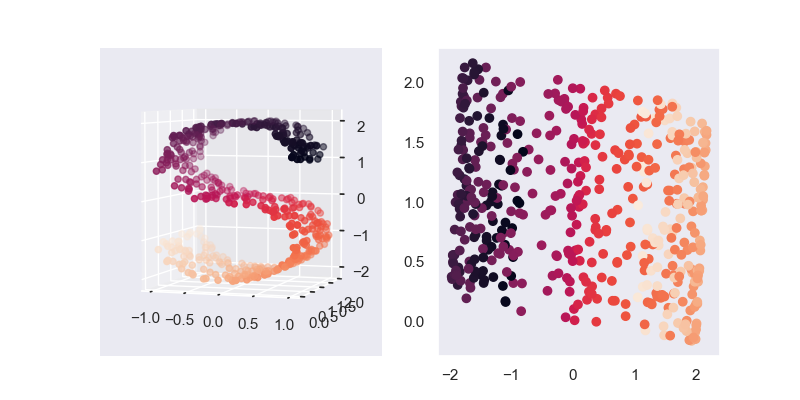
传统的SVD在降维前后,矩阵的维度并未发生变化,所以严格上SVD不能被称为数据降维,采用特征提取或者数据压缩的说法更为准确
上图仿照sklearn中SVD的做法,直接使用 \(A'=AV_k\) 实现真正意义上的降维
4. 模型推导
4.1. 基本定义
4.1.1. 数学表达
对于任意的矩阵 \(A\) ,一定可以分解为下列形式 \[ A = U \Sigma V^T \] 其中,\(U \in R^{m \times m}\) 称为左奇异矩阵, \(V \in R^{n \times n}\) 称为右奇异矩阵,\(U\) 和 \(V\) 都是单位正交矩阵,故有 \(U^TU = I,V^TV=I\);\(\Sigma \in R^{m \times n}\) 是一个仅主对角线上有值,其余部分为0的奇异值矩阵,其中,设对角线上的值为 \(\{\sigma_1,...,\sigma_{\min \{m,n\}}\}\) ,这是一组降序非负的序列,\(\sigma_i\) 称为 \(A\) 的奇异值
定义 \(A\) 的秩为 \(r \leq \min \{m, n\}\),设 \(k \leq r\),则取 \(U\) 和 \(V\) 的前 \(k\) 列组成矩阵 \(U_k \in R^{m \times k}, V_k \in R^{n \times k}\),以及 \(\Sigma\) 的前 \(k\) 行前 \(k\) 列组成矩阵 \(\Sigma_k \in R^{k \times k}\),则降维后的矩阵为 \[ A' =U_k \Sigma_k V^T_k \]
其中,如果 \(k = r\) ,则称其为紧(compact)SVD;如果 \(k < r\) ,则称其为截断(truncated)SVD
4.1.2. 物理意义
设空间中的一个基向量为 \(e\),则有,由于 \(U\) 和 \(V\) 都是正交矩阵, \(Ue\) 或 \(V^Te\) 表示对该向量的旋转变换;由于 \(\Sigma\) 是一个对角矩阵,则 \(\Sigma e\) 表示对该向量的各个维度的缩放变换。
设基向量 \(e_i \in R^n\),为了描述方便,下面假设 \(m>n\),则
\(V^Te_i\) 表示对 \(e_i\) 在 \(R^n\) 空间上进行一次旋转;\(\Sigma V^T e_i\) 表示对 \(V^Te_i\) 的每个维度都单独进行一次缩放,这里需要注意,由于 \(\Sigma \in R^{m \times n}\),所以缩放完后还需对向量扩展至 \(R^m\) 空间,只是由于 \(m-n\) 行全为0,所以这只是单纯的增加了 \(m-n\) 个维度;最后,\(U \Sigma V^T e_i\) 表示对 \(\Sigma V^T e_i\) 在 \(R^m\) 空间上进行一次旋转。
经过上述变换,我们就得到了一个向量 \(a_i \in R^m\) ,这便是矩阵 \(A\) 中一个特征维度的所有信息;对空间中的 \(n\) 个基向量 \(e_i\) 都进行如上操作,得到的 \(n\) 个向量便组成了一个空间矩阵 \(A\)
现在来看 \(U_k \Sigma_k V^T_k e_i\)
\(V^T_ke_i\) 表示对 \(e_i\) 仍按原计划进行旋转,但旋转完后,对于 \(n-k\) 的维度的信息直接去掉,即将其垂直投影至 \(R^k\) 空间中(这一步的解析性不强的,因为我们并不能确定比其他维度的信息一定比高维度的信息多,所以这有一种碰运气的感觉);接着对 \(V^T_ke_i\) 进行缩放,注意 \(\Sigma\) 矩阵对角线的值是降序的,所以高纬度的变换量是比较少的,这样就可以尽可能减少信息的损失量,所以这一步是可以解释得通的; 最终再进行一次旋转,注意这里旋转完后需要进行扩维,但由于是垂直映射到高维空间,所以会增加一些0值。
SVD降维使得矩阵中的某些值会变为0,最终矩阵变得稀疏了,即数据量被压缩了。
4.2. 学习策略
最终问题只剩下3个奇异矩阵的求解了,下面介绍一种简单的计算流程
首先,我们应当注意到 \(U^TU = I,V^TV=I\),故 \(A\) 具有如下性质 \[ A A^{T}=U \Sigma V^{T} V \Sigma^{T} U^{T}=U \Sigma \Sigma^{T} U^{T} \\ A^{T} A=V \Sigma^{T} U^{T} U \Sigma V^{T}=V \Sigma^{T} \Sigma V^{T} \] 注意到 \(\Sigma^T \Sigma = \Sigma \Sigma^T = \Sigma^2\),故有 \[ (AA^T)u_i = \sigma_i^2 u_i \\ (A^TA)v_i = \sigma_i^2 v_i \] 可以看出 \(u_i\) 是 \(AA^T\) 的一个特征向量,\(v_i\) 是 \(A^TA\) 的一个特征向量
这启发我们可以通过求 \(AA^T\) 的m个特征列向量组成 \(U\) 以及求 \(A^TA\) 的n个特征列向量组成 \(V\)
最后,如果 \(m > n\) ,则取 \(A^TA\) 的特征值降序排序,组成 \(\Sigma\) 矩阵;反之,则取 \(AA^T\) 的特征值降序排序,组成 \(\Sigma\) 矩阵
4.3. 学习算法
最终算法流程总结如下:
- 计算 \(A^TA\) 的n个特征值 \(\lambda\) 和单位特征向量 \(v\),按 \(\lambda\) 降序排序,用 \(v\) 构成正交矩阵 \(V=\{v_1,...,v_n\}\)
- 计算 \(AA^T\) 的m个特征值 \(\lambda\) 和单位特征向量 \(u\),按 \(\lambda\) 降序排序,用 \(u\) 构成正交矩阵 \(U=\{u_1,...,u_m\}\)
- 取上面计算结果的前 \(\min \{m,n\}\) 个 \(\lambda\) 值,组成对角矩阵 \(\Sigma = \text{diag}(\{\sqrt{\lambda_1},...,\sqrt{\lambda_{\min \{m,n\}}}\})\)
- 取 \(U\) 和 \(V\) 的前 \(k\) 列组成矩阵 \(U_k \in R^{m \times k}, V_k \in R^{n \times k}\),以及 \(\Sigma\) 的前 \(k\) 行前 \(k\) 列组成矩阵 \(\Sigma_k \in R^{k \times k}\)
- 计算降维矩阵 \(A' =U_k \Sigma_k V^T_k\)
5. references
《统计学习方法》15章,李航