本来和神经网络-CNN基础为同一篇笔记,但由于篇幅太长,故将其一拆为二,另起一篇
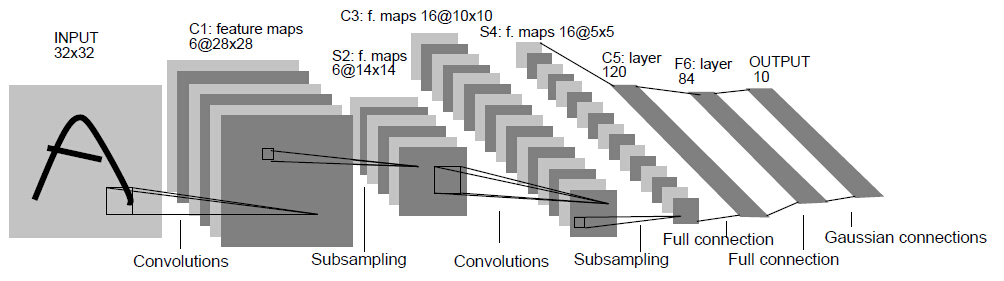
1. LeNet
1989年的论文(比我的年龄还大(⊙ˍ⊙)):
- Handwritten Digit Recognition with a Back-Propagation Network
- Backpropagation Applied to Handwritten Zip Code Recognition
个人基于pytorch的实现代码
网络结构:
卷积神经网络的奠基之作,提出了CNN网络一些最基础的概念:卷积、池化、全连接、反向传播等
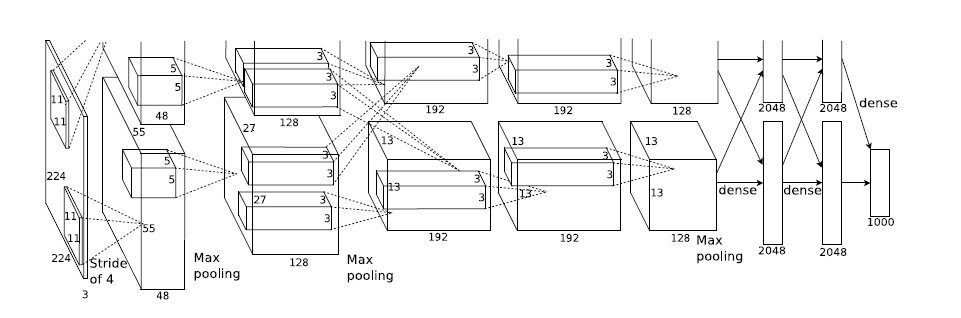
2. AlexNet
ISLVRC 2012的分类任务组冠军:ImageNet Classification with Deep Convolutional Neural Networks
个人基于pytorch的实现代码
网络结构:
这是最经典的CNN网络,拥有更深的网络,且增加了ReLU和Dropout
2.1. Local Response Normalization
论文中还提出一个局部响应归一化(Local Response Normalization,LRN)层,计算公式 \[ b_{x, y}^{i}=a_{x, y}^{i} /\left(k+\alpha \sum_{j=\max (0, i-n / 2)}^{\min (N-1, i+n / 2)}\left(a_{x, y}^{j}\right)^{2}\right)^{\beta} \] 其中,\(a_{x, y}^{i}\) 为输出通道 \(i\) 在位置 \((x,y)\) 处的原始值,\(b_{x, y}^{i}\) 为归一化之后的值。\(n\) 为影响第 \(i\) 个通道的通道数量(分别从左侧、右侧 \(n/2\) 个通道考虑)。\(\alpha,\beta,k\) 为超参数。论文中取 \(k=2,n=5,\alpha=10^{-4},\beta=0.75\)
该层的基本思想是,输出通道 \(i\) 在位置 \((x,y)\) 处的输出会受到相邻通道在相同位置输出的影响。达到横向抑制的效果,即使得不同的卷积核所获得的响应产生竞争
但现在一般认为该结构用处不大(VGG中有相关的证明),只会增加网络的运算量,所以现在该结构很少被使用
2.2. Overlapping Pooling
一般池化都是不重叠的,即步长大于pooling size。AlexNet中允许可重叠的池化,即步长小于pooling size,并认为这种做法可以轻微的减轻过拟合的问题。
对此,一种观点认为,重叠池化会带来更多的特征,这些特征很可能会有利于提高模型的泛化能力。
2.3. Data Augmentation
- 统一尺寸。先对图片等比resize,使短边至固定长度;然后裁剪长边,使其与短边相等,便得到了一个大小固定的矩形图片
- 尺寸修剪。训练阶段,对同一张图片进行随机性的裁剪(256->224),然后随机水平翻转;预测阶段,裁剪出四个角落位置、一个中心位置,再加上水平翻转的图片,共10张裁剪后图片(256->224)。预测结果的均值作为最终的预测输出
- 颜色抖动。裁剪翻转的图片,经过PCA降维去噪后,放大一个随机(服从 \(N(0,0.1)\) 正态分布)的因子倍数 \(\alpha\),即 \(\left[\mathbf{p}_1, \mathbf{p}_2, \mathbf{p}_3\right]\left[\alpha_1 \lambda_1, \alpha_2 \lambda_2, \alpha_3 \lambda_3\right]^T\),其中,\(\mathbf{p}_i,\lambda_i\) 分别为PCA降维后的特征向量矩阵和特征值
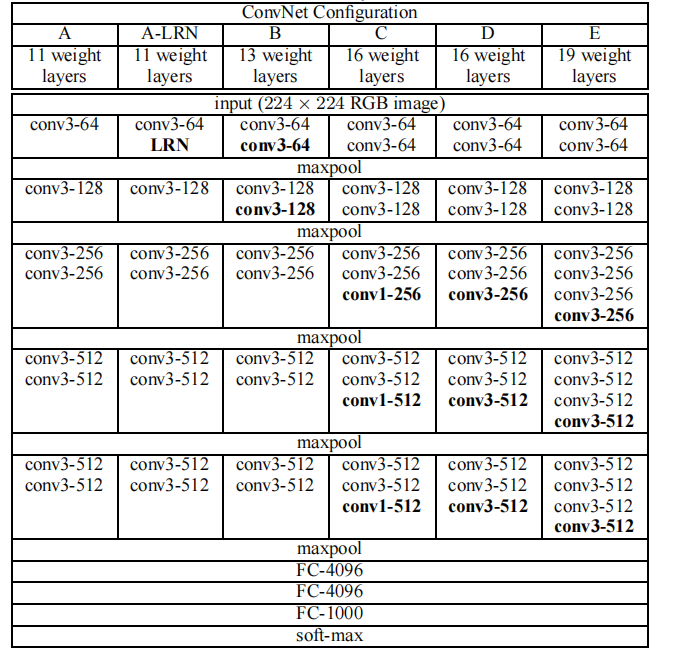
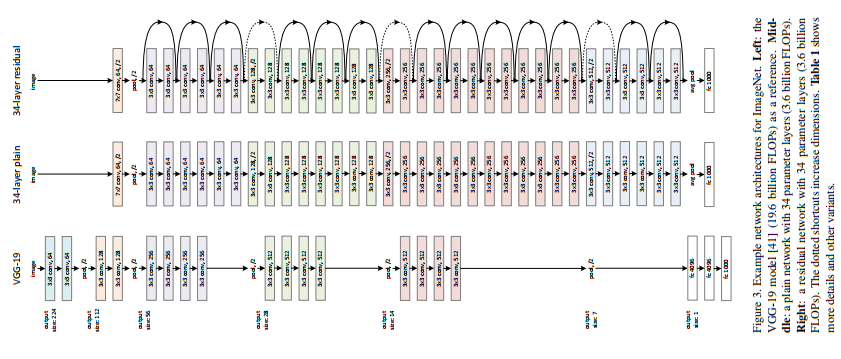
3. VGG-Net
ILSVRC 2014的分类任务组亚军:Very Deep Convolutional Networks for Large-Scale Image Recognition
个人基于pytorch的实现代码
网络结构:
3.1. 小卷积核
一般来说,卷积核越大,感受野面积越大,获取到的特征越好。但卷积核越大,需要训练的参数也越大。而VGG则证明了小尺寸卷积核的深层网络要优于大尺寸卷积核的浅层网络,这也是这篇论文最大的贡献
使用多个小卷积核取代一个大的卷积核,需要训练的参数量大大减少。例如,一个 \(5\times 5\) 的卷积核,要使得输出的特征图面积不变,则需要2个 \(3\times 3\) 的卷积核替代,而替代后的参数只有原来的 \(\frac{2 \times 3 \times 3}{5\times 5} = 0.72\) 倍
另外,论文中也证明了深度对网络的泛化性能的重要性
3.2. 尺寸抖动(scale jittering)
论文采用的数据增强方式:训练前选取一个随机值 \(S \in [S_{\min},S_{\max}]\) ,等比resize,使短边为 \(S\),然后再裁剪成固定尺寸的图片。
论文通过实验认为,相比resize固定短边后再裁剪成固定尺寸图片的方式,scale jittering可以显著提升模型效果
除了尺寸抖动的方式,为了应对多尺度图片输入,论文还训练了多个不同尺度输入的模型,然后对这些网络的结果求平均。
注:大尺寸的网络是在小网络的基础上finetune出来的,但论文认为这只是为了节省时间,就是不承认finetune,啧啧啧~
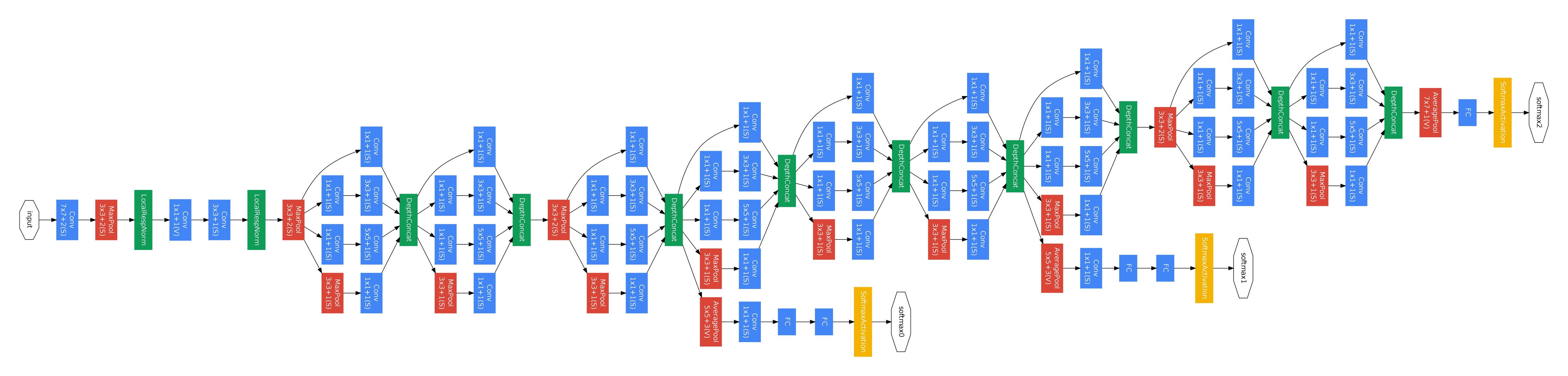
4. GoogLeNet(Inception系列)
ILSVRC 2014的分类任务组冠军:Going deeper with convolutions
这篇论文其实是专门讲Inception的,GoogLeNet只是顺带提一下。另外,GoogLeNet中L是大写,是为向LeCuns做出的贡献表示敬意。
网络结构:
4.1. Inception
个人基于pytorch的实现代码
Inception原义有开端、全面启动等意思,还有一部电影也叫Inception,译名盗梦空间,作者取这个名字,除了受到电影中“We need to go deeper”台词的影响,是不是也展示了他对该结构的自信与野心?事实上,这的确是一个很富有开端式的结构
当时的CNN都是通过堆叠串联卷积层,将网络做深,是模型具有更好的性能。但网络变深,一方面意味着过拟合变严重,另一方面计算量也变大。
GoogLeNet应用了一种Inception结构,这种结构将串行的卷积层变成并行的,然后再将每个卷积层的结构耦合(沿深度方向拼接)在一起。具体结构如下:
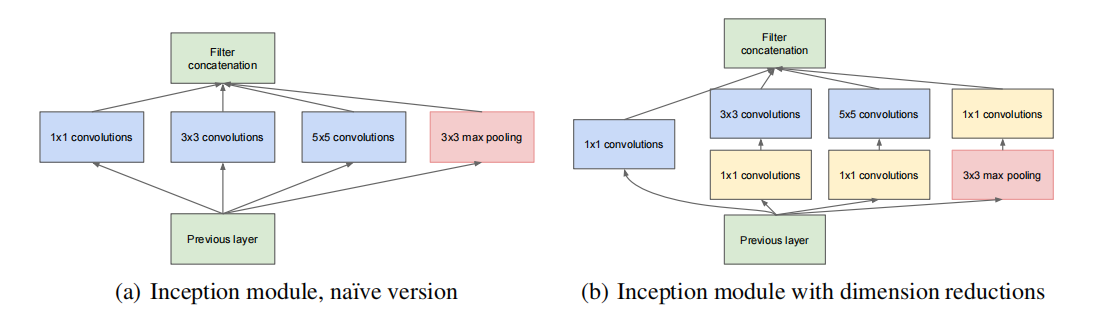
最原始的Inception结构如图a所示,3个不同尺寸的卷积层并行计算,其输出特征图然后再按高度拼接到一起。为了使得输出的特征图大小一致,需要进行padding操作。另外,结构还直接拼接了一个最大池化层,这一层是为了获取输入的原始特征。
拼接一个简单的卷积层或池化层的操作,就很有后面resnet提出的残差层那味了
另外,网络结构每一层的参数没有太多的规律,看来是使用了一些网络搜索的技巧。
论文中认为原始的结构最终的通道数可能会太大了,所以预先分别输入一个 \(1*1\) 的卷积层进行降维,所以这是一种稀疏连接。有一点需要注意的是,需要先池化再进行降维,这是因为先降维,池化不是获取最原始的输入特征了。
Inception结构从网络的宽度入手,将串行变成并行,一方面降低模型的深度,减轻过拟合程度;另一方面有利于集群并行计算,侧面降低了计算成本。
4.2. Inception V2
2015年的论文:Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
个人基于pytorch的实现代码
注:Inception V2以及后面的Inception系列已经不包含在GoogLeNet中,这里为了方便,都写在同一个章节里面。
该论文提出了经典的批次归一化(Batch Normalization,BN)处理
前向计算:
反向计算:
优点:
- 加快训练速度
- 提高模型泛化能力
除了BN,后面还提出了layer normalization(LN),以及其他各种的normalization。其实就是一个立方体,无论是正切、反切、斜切、对半切,其实都可以。只要结果是work的,再倒回来自圆其说就可以了。
4.3. Inception V3
2015年的论文:Rethinking the Inception Architecture for Computer Vision
个人基于pytorch的实现代码
注:网上找资料的时候,有一些材料认为这是Inception V2,而且论文里面有一个章节说这是Inception V2的结构。但我网上并未找到其他Inception V3的结构,如果这是Inception V2,那如果这是Inception V3的结构长什么样呢?所以这个地方先存疑。
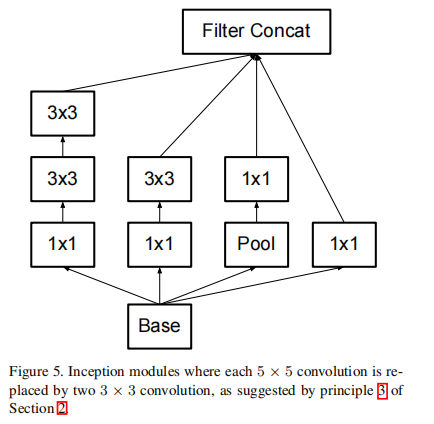
将大卷积核转换成小卷积核,这个在VGG中已经讲过了
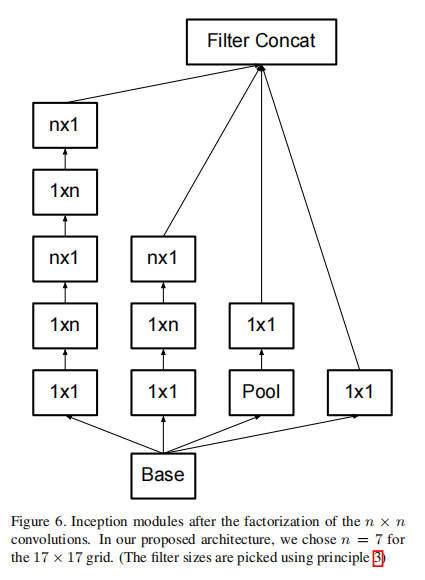
论文中还提出将大卷积转换成非对称式的卷积核,即将一个 \(n \times n\) 的卷积核转换成一个 \(1 \times n\) 和一个 \(n \times 1\) 的卷积核,从而减少训练参数。
这是一个很巧妙的设计,一个大卷积核拆成两个非对称的卷积核后,两者最终输出特征图的大小是一样的,但参数后者只有前者的 \(\frac{2}{n}\)
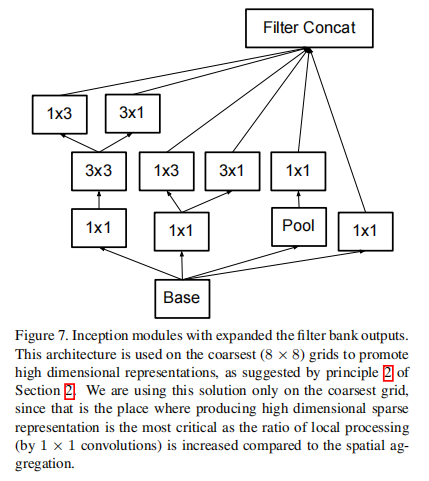
一不做二不休,论文最后还继续将两个非对称的卷积核改成并联模式(有点丧心病狂了:-))
4.4. Inception V4 & Inception-ResNet
2016年的论文:Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning
该论文同时提出了两种结构:Inception V4 和 Inception-ResNet
Inception V4,总体没有太大的改进,就是在v3的基础上增加或减少一些卷积层,缝缝补补(非常能体现搭积木的思想)。整体结构图如下:
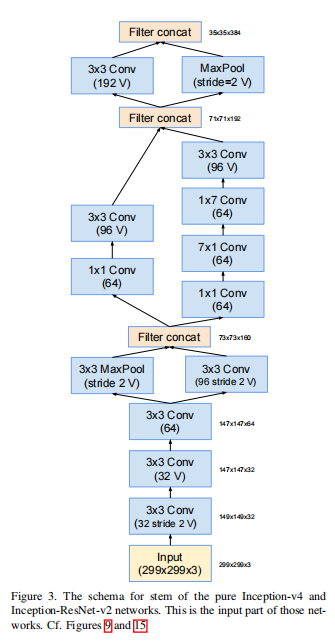
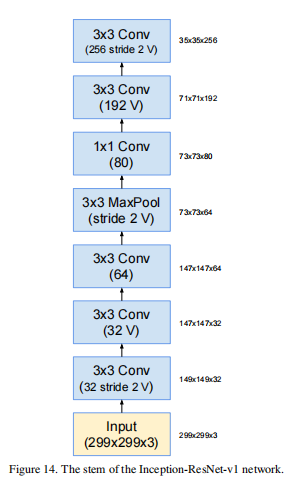
其中Inception-A/B/C以及Reduction-A/B都是一些比较基础的Inception结构,这里就不放结构图了,直接看论文就可以了。下面挑一些stem的结构进行展示:
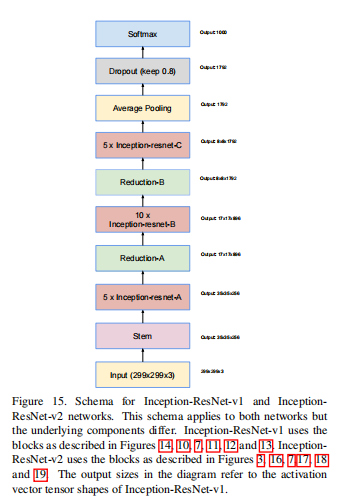
Inception-ResNet,就是结合了ResNet的残差结构。残差结构放在ResNet章节中重点分析,下面直接给出网络结构图:
stem结构:
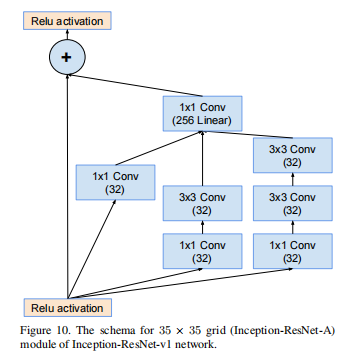
Inception-ResNet-A结构:
4.5. Xception
2016年的论文:Xception: Deep Learning with Depthwise Separable Convolutions
Xception,即Extreme Inception,将每个通道使用一个filter,改为所有通道共用一个filter,即
- simple Inception:\([D_W \cdot D_H \cdot M] * [1 \cdot 1 \cdot M \cdot N] * [D_{K} \cdot D_{K} \cdot N \cdot M] \rightarrow [D_W \cdot D_H \cdot M]\)
- Xception:\([D_W \cdot D_H \cdot M] * [1 \cdot 1 \cdot 1 \cdot M] * [D_{K} \cdot D_{K} \cdot 1 \cdot M] \rightarrow [D_W \cdot D_H \cdot M]\)
优点:
- 减少的参数量,降低了模型复杂度
- 加强了通道相关性和空间相关性
5. ResNet
CVPR 2016的最佳论文:Deep Residual Learning for Image Recognition
个人基于pytorch的实现代码
网络结构:
5.1. Deep Residual Learning
论文发现,当模型加深的时候,除了会引起梯度爆炸/消失问题(这个问题已经在Inception V2中通过BN有所减轻),还会引起网络退化的问题。
所谓的网络退化,就是上一层网络的误差不断累积到下一层,随着网络加深,网络逐渐偏离原来问题的中心(准确率达到饱和并有下降趋势),甚至已经退化成解决其他问题的网络。
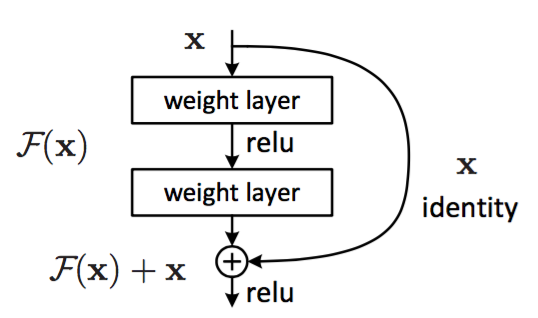
于是,论文中提出了大名鼎鼎的残差结构(如下图所示)来对抗网络退化问题。
数学表达式 \[ x_l=\mathcal{F}\left(x_{l-1},W_{k}\right)+W_{s} x_{l-1} \] 该结构包括两部分内容:残差表示(Residual Representations) 和 短路连接(Shortcut Connections)。其中,
- 残差表示就是 \(F(x) + x\) 的表达形式;
- 短路连接就是输入和输出直接耦合的做法,就像电路的短路一样。
对于残差结构的作用,
一种具象化的解释是:下一层耦合了上一层的数据后,下一层网络其实需要完成两个任务。一个是对上一层输入的优化,一个是对上一层输出的优化。或者说,网络参考着上一层的优化结果,重新对问题进行优化,从而将网络重新拉回问题中心,从而可以对抗网络退化。
从数学推导上分析,普遍的观点认为残差结构通过减轻梯度消失来对抗网络退化。因为在反向传播中,有 \[ \frac{\partial x_l}{\partial x_{l-1}} = W_s \cdot 1 + \frac{\partial }{\partial x_{l-1}}(\sum \mathcal{F_i}) \] 可以看到,原始输入的梯度被完整的传递下去了,保证了梯度不会消失
5.2. bottleneck
为了节省训练时间,当网络比较深时,论文将两层卷积的残差结构改为三层的。其中第一个1x1卷积用于降维,中间的3x3卷积用于提取信息,最后一个1x1卷积用于升维。
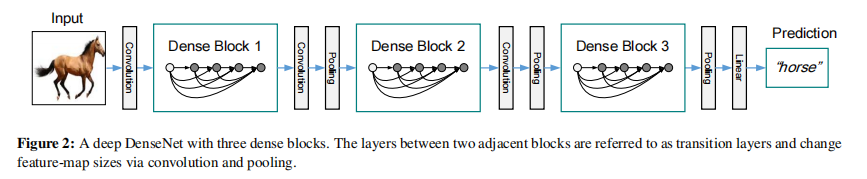
6. DenseNet
CVPR 2017的最佳论文:Densely Connected Convolutional Networks
代码实现:
网络结构:
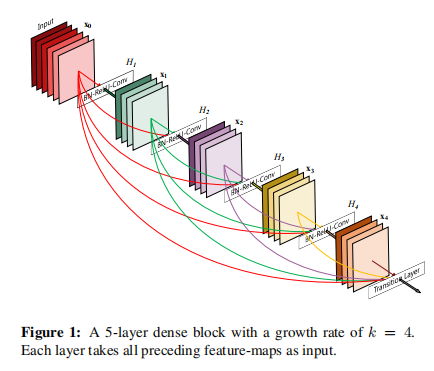
6.1. Dense Block
ResNet残差结构的升级版,其结构如下:
数学表达式 \[ x_l=\mathcal{F}\left(x_{l-1},W_{k}\right)+ \sum_{i=0}^{l-1} W_{i} x_{i} \] ResNet是只与前面一层相连,而DenseNet则索性将当前层与前面所有层直接相连,非常稠密(dense),DenseNet称这样的处理为特征重用(feature reuse)
优点:
- 可以比ResNet在参数和计算成本更少的情形下拥有更优的性能
- 更进一步的减轻梯度消失的问题,是网络更加容易训练,提升网络的学习能力
7. SENet
ILSVRC 2017分类任务组冠军:Squeeze-and-Excitation Networks
代码实现:
这篇论文最大的亮点是提出了一个Squeeze-Excitation(SE) block的结构,这种结构可以很好的嵌入到众多主流的CNN框架(如Inception、ResNet等)中,并提高了网络的表达能力
7.1. SE block
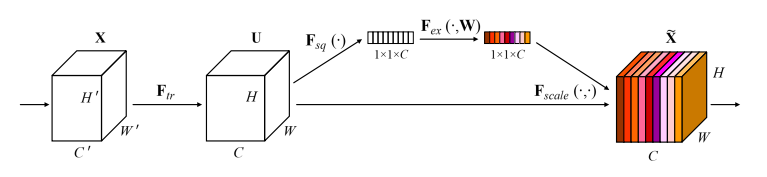
通过显式地对通道之间的相互依赖关系建模,自适应的重新校准通道维度的特征响应,从而提高了网络的表达能力
Transformation。一些卷积操作 \[ \mathbf{u}_{c} = \mathbf{F}_{tr}\left(\mathbf{v}_{c}\right) = \mathbf{v}_{c} * \mathbf{X} \]
Squeeze。一个global pooling,分别对每个通道求平均,即 \[ z_{c}=\mathbf{F}_{s q}\left(\mathbf{u}_{c}\right)=\frac{1}{H \times W} \sum_{i=1}^{H} \sum_{j=1}^{W} \mathbf{u}_{c}(i, j) \] 这一步将一个三维的矩阵压缩成一个一维的向量编码,可以理解为每个通道的权重。
Excitation。这一步实际上是两个全连接层,即 \[ \mathbf{s}=\mathbf{F}_{e x}(\mathbf{z}, \mathbf{W})=\sigma(g(\mathbf{z}, \mathbf{W}))=\sigma\left(\mathbf{W}_{2} \delta\left(\mathbf{W}_{1} \mathbf{z}\right)\right) \\ where\quad \delta = Relu,\sigma = Sigmoid,\mathbf{W}_1 \in \mathbb R^{\frac{C}{r} \times C},\mathbf{W}_2 \in \mathbb R^{C \times \frac{C}{r}} \] 可以理解为通过先降维再升维,来提高网络的泛化能力。
Scale。用输入乘上权重,得到最终输出,即 \[ \widetilde{\mathbf{x}}_{c}=\mathbf{F}_{\text {scale }}\left(\mathbf{u}_{c}, s_{c}\right)=s_{c} \mathbf{u}_{c} \]
论文中认为这实际上就是一种attention的机制。
8. SqueezeNet
2016年的论文:Squeezenet: Alexnet-level accuracy with 50x fewer parameters and< 0.5 mb model size
代码实现:
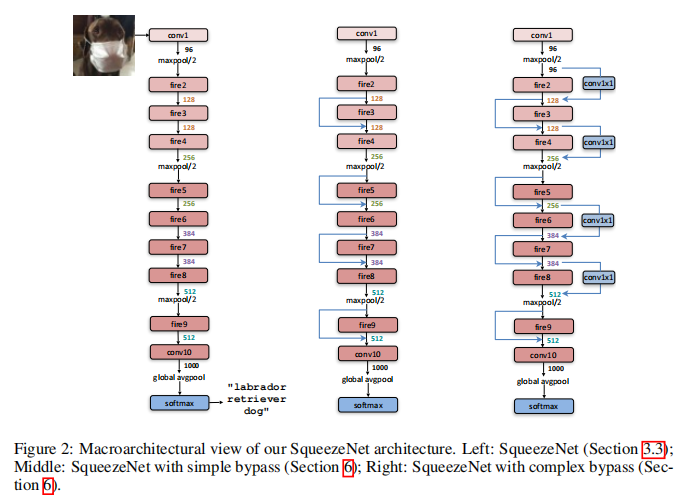
网络结构:
SqueezeNet是一个轻量化的网路,论文题目也非常直白:我就是冲着网络轻量化去的。
一般为了获得更好的效果,都是将神经网络做大做深。但随着移动端的崛起,神经网络也逐渐往轻量化方向发展。
一个轻量化模型的标准:数据量小于150 MFLOPs(一次前向推断需要n百万次浮点运算)
8.1. Fire module
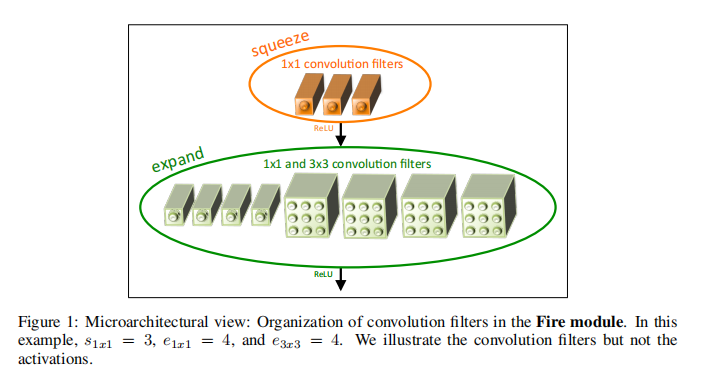
SqueezeNet的核心是fire module,其结构如下:
其包含两部分操作:
- squeeze,普通的 \(1 \times 1\) 的卷积层
- expand,将一部分 \(3 \times 3\) 的卷积核直接削减成 \(1 \times 1\) 的卷积核,然后将两部分的结果沿深度拼接
减少参数量的方法非常简单粗暴,就是直接缩小卷积核的尺寸,然后做了下实验,发现参数少了50倍,但模型效果只降低一点,这笔买卖非常合得来。
其实也从侧面说明,对于一些数据量不大的任务,完全没必要使用很大的卷积核,即使是最简单的 \(1 \times 1\) 的卷积层(这是其实就变成全连接层了)也是足以胜任的。
8.2. 模型压缩
SqueezeNet还使用了一些模型压缩的算法,如SVD,网络剪枝(network pruning)和量化(quantization)等,这里就不展开讲了
9. MobileNet系列
MobileNet也是一个轻量化的神经网络。
9.1. MobileNet V1
2017年的论文:MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
个人基于pytorch的实现代码
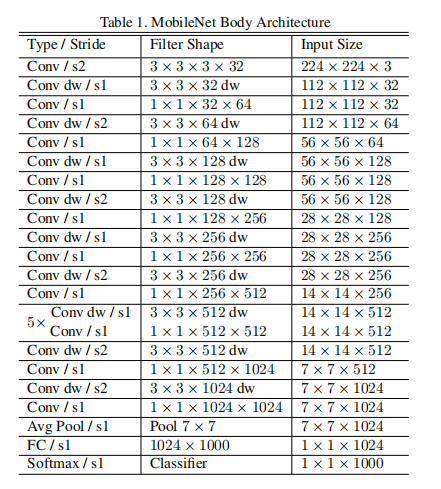
网络结构:
注:
上表中,倒数第3、4层的input size有误,应为4x4x1024
MobileNet的结构和Xception的结构是很像的,而MobileNet的发表时间比Xception稍晚,但据说当时是两个团队同时研究,但MobileNet的发表较晚。而且都是同一个公司的出品,其实也不存在谁抄袭谁的说法了,只能说研究方向撞车了。
另外,两者最大的不同之处是MobileNet是先depthwise再pointwise;而Xception是先pointwise再depthwise
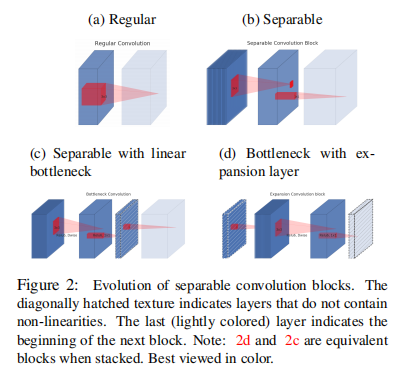
9.1.1. Depthwise Separable Convolution
使用深度可分离卷积(Depthwise Separable Convolution)替换普通卷积,两者的计算流程(默认padding)分别为:
- 普通卷积:\([D_W \cdot D_H \cdot M] * [D_{K} \cdot D_{K} \cdot M \cdot N] \rightarrow [D_W \cdot D_H \cdot N]\)
- 深度可分离卷积:\([D_W \cdot D_H \cdot M] * [D_{K} \cdot D_{K} \cdot 1 \cdot M] * [1 \cdot 1 \cdot M \cdot N] \rightarrow [D_W \cdot D_H \cdot N]\)
可以看出,深度可分离卷积将卷积计算分成了两部分,其中,\([D_{K} \cdot D_{K} \cdot 1 \cdot M]\) 部分的卷积称为深度(depthwise)卷积;\([1 \cdot 1 \cdot M \cdot N]\) 部分的卷积称为逐点(pointwise)卷积
参数量和计算量替换前后(分子替换前,分母替换后)比较: \[ \text{参数量比} = \frac{D_{K} \cdot D_{K} \cdot M +M \cdot N }{D_{K} \cdot D_{K} \cdot M \cdot N } =\frac{1}{N}+\frac{1}{D_{K}^{2}} \\ \text{计算量比} = \frac{D_{K} \cdot D_{K} \cdot M \cdot D_W \cdot D_H +M \cdot N \cdot D_W \cdot D_H}{D_{K} \cdot D_{K} \cdot M \cdot N \cdot D_W \cdot D_H} = \frac{1}{N}+\frac{1}{D_{K}^{2}} \] 可以看出,在保持最终输出的特征图大小一致的前提下,参数量和计算量比较都下降了 \(\frac{1}{N}+\frac{1}{D_{K}^{2}}\),例如,常用的 \(3\times3\) 卷积核,下降量为八分之一左右。
9.1.2. width multiplier & resolution multiplier
- width multiplier,宽度因子 \(\alpha\),等比例降低输入输出的通道数,参数量下降 \(\alpha^2\) ,计算量不变
- resolution multiplier,分辨率因子 \(\rho\),等比例降低输入输出的尺寸,参数量不变,计算量下降 \(\rho^2\)
其实我没太懂论文中为什么要把这部分的内容单独拿出来讲,这难道不就是很普通的工程调参吗?
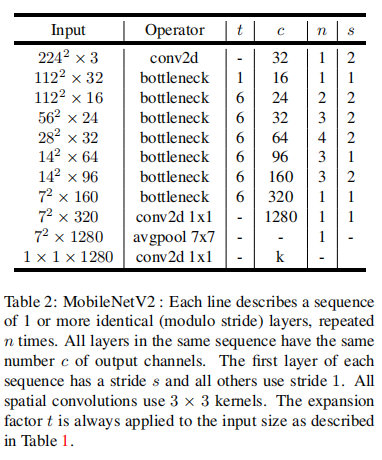
9.2. MobileNet V2
2019年的论文:MobileNetV2: Inverted Residuals and Linear Bottlenecks
网络结构:
9.2.1. Linear Bottlenecks
论文中认为,由于ReLU激活函数的存在,某些通道可能会被全部都置0,从而出现不可逆的信息损失。所以应该在最后几层设置一些不使用激活函数的瓶颈(bottlenecks)层,即所谓的线性瓶颈(Linear Bottlenecks)结构。
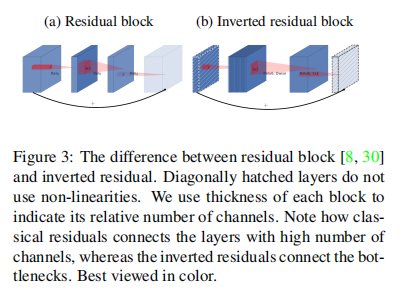
9.2.2. Inverted residuals
一般的残差结构会使用一个\(1 \times 1\)的卷积核降维,而反转残差(Inverted residuals)结构,则先使用一个\(1 \times 1\)的卷积核升维,然后是卷积操作,最后再使用一个\(1 \times 1\) 的卷积核降维至原来的大小。
需要注意的是,最后一步的降维操作不需要使用激活函数,是一个瓶颈层。
9.2.3. ReLU6
ReLU6对比ReLU增加了一个上界,其表达式为 \[ \text{ReLU(6)} = \min (\max (0,x),6) \] 作者认为ReLU6在低精度计算下具有更强的鲁棒性
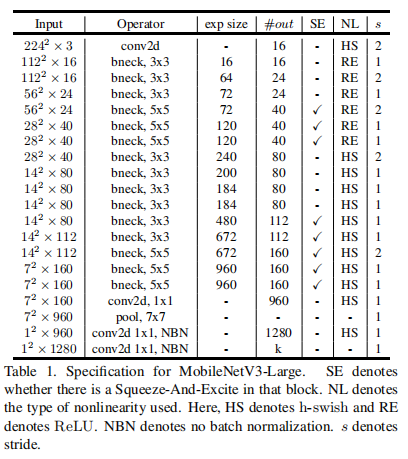
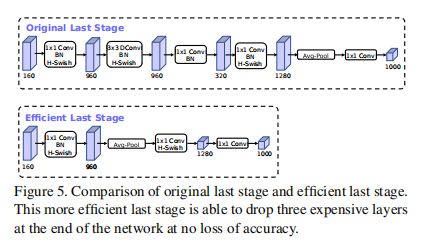
9.3. MobileNet V3
2019年的论文:Searching for MobileNetV3
网络结构(Large):
一个很有趣的点是,V3的网络结构是使用NetAdapt算法优化出来的
9.3.1. bneck
直接将V2版本的瓶颈层去掉
9.3.2. h-wish
hard swish(h-wish)是使用近似模拟swish和ReLU函数得出的,其表达式: \[ \operatorname{h-swish}(x)=x \frac{\operatorname{ReLU} 6(x+3)}{6} \] 但论文研究发现,h-wish只在深层网络中效果更好,考虑到其计算成本,所以网络前半部分使用ReLU,后半部分使用h-wish
10. ShuffleNet系列
10.1. ShuffleNet V1
2017年的论文:ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices
代码实现:
论文中发现,像ResNet、MobileNet等网络,计算量占比最大的是 \(1 \times 1\) 的卷积层(约93%的计算量),为此,论文提出采用分组卷积的方式,减少网络的参数。
例如,对于一个输入深度为 \(M\) 、输出深度为 \(N\) 的任务,则需要 \(N\) 个 \(1\times 1 \times M\) 的卷积核,先按通道对输入分成 \(G\) 个组,然后再进行分组卷积,则只需 \(N\) 个 \(1\times 1 \times M/G\) 的卷积核
但每次都按固定分组卷积,每个卷积核学到的都是固定分组内的信息,阻止通道之间的信息流动,降低网络的表达能力。所以在每次分组前,还应该按通道打乱(论文中采用的并非随机打乱,而是有序的打乱,具体的打乱规则见下图),当迭代次数增大时,每个卷积核还是能看到所有通道的信息的
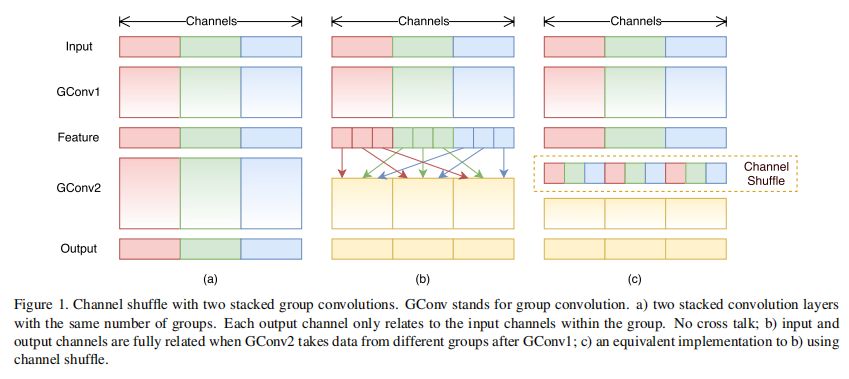
10.2. ShuffleNet V2
2018年的论文:ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design
官方代码:https://github.com/megvii-model/ShuffleNet-Series
论文中指出除了计算量,内存使用量(memory access cost, MAC)同样会影响计算速度。论文中还提出了四个模型轻量化的指导准则:
- 输入输出通道数相等时,MAC最小
- 过量使用分组卷积会增大MAC
- 网络分支会降低并行度
- 不能忽视元素级操作(例如ReLU、求和等)的影响
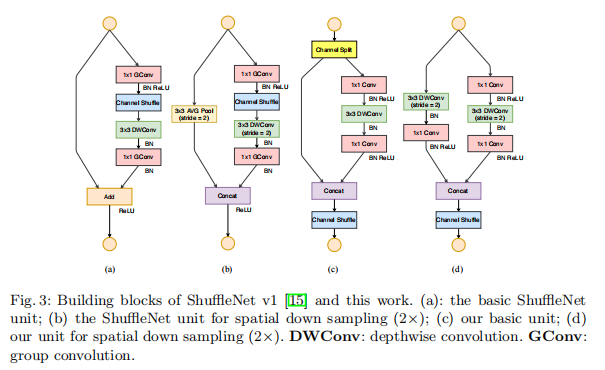
针对上述的准则,论文中提出了改进版的ShuffleNet模块
主要改进点:
- 取消 \(1 \times 1\) 的分组卷积,而只保留 \(3 \times 3\) 的分组卷积
- 左右两路特征图不再相加,都改为直接拼接
- 分组打乱移到拼接操作之后
11. IGC系列
IGC系列是分组卷积的集大成者
11.1. IGC V1
2017年的论文:Interleaved Group Convolutions for Deep Neural Networks
个人基于pytorch的实现代码
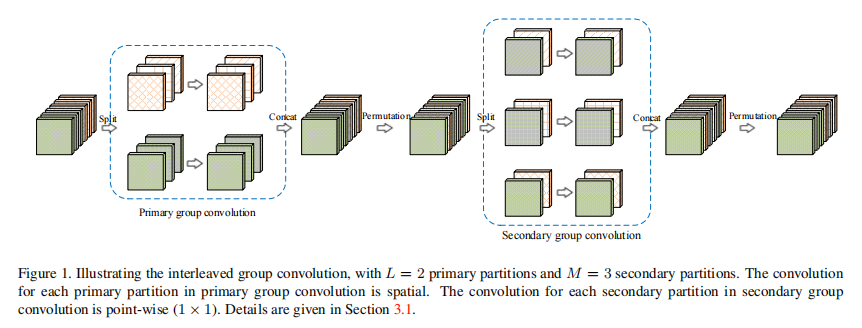
交错组卷积(Interleaved Group Convolutions,IGC)分成两个部分:
- Primary group convolutions,使用 \(3 \times 3\) 的分组卷积,主要用来提取特征
- Secondary group convolutions,使用 \(1 \times 1\) 的分组卷积,主要用来处理通道间的相关性
这两层分组卷积是互补交错的,例如,第一层分组数为 \(L\),每个分组的通道数为 \(M\);则第二层分组数为 \(M\),每个分组的通道数为 \(L\)。
论文中认为这样的互补结构可以减少网络的冗余性
11.2. IGC V2
2018年的论文:IGCV2: Interleaved Structured Sparse Convolutional Neural Networks
在V1中,一般第一层分组卷积的分组数较少,而通道数较多,这导致了第二层分组卷积的分组数较多,过于稠密。
于是,V2抛弃了原先两层分组的结构,改为若干个连续的稀疏的分组卷积,更加具体的,将其写成数学表达式为 \[ y = P_L W_L \cdots P_1 W_1 x \] 其中,\(P_l\) 表示交错重排,\(W_l\) 表示分组卷积
可以看出来和ShuffleNet的做法是很像的,只能说又撞车了。
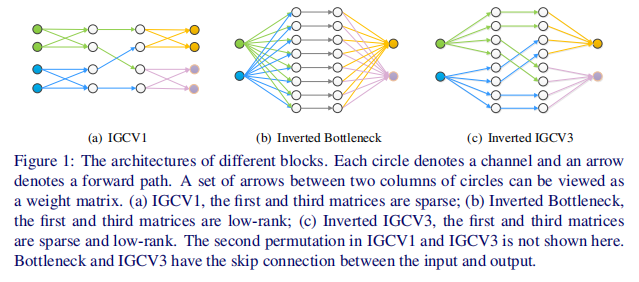
11.3. IGC V3
2018年的论文:IGCV3: Interleaved Low-Rank Group Convolutions for Efficient Deep Neural Networks
官方代码:https://github.com/homles11/IGCV3
V3借鉴了MobileNet V2的Inverted residuals结构,再结合分组卷积,整体流程如下
- 进行 \(1\times 1\) 的分组卷积升维
- 先进行普通的分组卷积,然后重排
- 进行 \(1\times 1\) 的分组卷积降维至原来的维度
因为是bottleneck结构,所以上述的卷积操作都不需要加激活函数
12. CondenseNet系列
12.1. CondenseNet V1
CVPR 2018的论文:CondenseNet: An Efficient DenseNet using Learned Group Convolutions
代码实现:
denseNet+ShuffleNet的混合体。
论文中认为像denseNet那样的连接密度太高了,里面存在着很多的冗余计算,所以可以尝试加入类似ShuffleNet的分组卷积结构,降低计算的冗余。但通过实验,论文发现,如果只对 \(3 \times 3\) 使用分组卷积,对模型效果影响不大;但如果只对 \(1 \times 1\) 使用分组卷积,模型效果会下降很多。论文认为原因可能是:
- 通道间并非独立,存在一定的顺序性及相关性,随便分配会打乱这种顺序
- 每个通道存在着一定的多样性,如果随便分配到不相交的组,会降低特征的重用性
- 尽管使用了shuffle的策略,但每个卷积核仍然无法看到全局的特征,这里会存在不少的信息损失
所以,要减轻分组带来的影响,一种最直接的方案就是减少分组对通道间相关性的干扰。
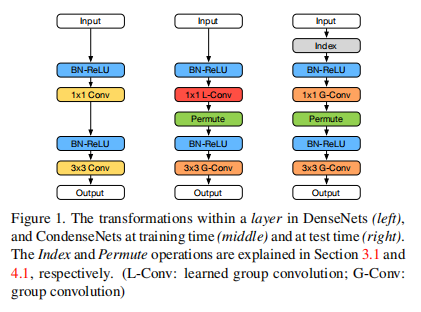
论文中提出一个分组的思路,对于 \(1 \times 1\) 的卷积层,训练的时候使用自学习分组卷积(Learned Group Convolution,LGC),得到一个关于输入通道的权重编码;而测试的时候直接使用该权重编码直接进行分组卷积,如下所示
其中,LGC结构如下
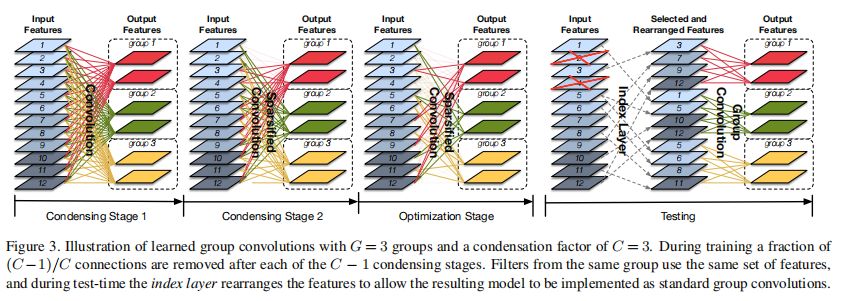
当模型迭代到一定的次数的时候,会进入一个mask的stage,该stage又分为浓缩(Condensation)和优化(optimization)两个阶段
浓缩阶段:
Filter Groups,对 \(1\times 1\) 的卷积核分组。这里的分组和ShuffleNet的对feature进行分组有所区别。前者卷积核没变,后者卷积核变小了。
Condensation Criterion,计算每个分组内的各个通道的L1范式作为权值,即\(\sum_{i=1}^{O / G} |\mathbf{F}_{i, j}^{g}|\),其中,\(G\)是分组数,\(O\) 是输出通道数。
Group Lasso,计算置0操作所带来的损失,用于反向求解 \[ \sum_{g=1}^{G} \sum_{j=1}^{R} \sqrt{\sum_{i=1}^{O / G} (\mathbf{F}_{i, j}^{g})^2} \]
优化阶段
- Condensation Factor,设定一个浓缩因子 \(C\),该值表示一共需要经过 \(C-1\) 次stage
- Condensation Procedure,丢弃权值较小的 \(I/C\) 个通道,其中,\(I\) 为输入通道数。这意味着最终只能拿到一个最多只保留 \(I/C\) 个有效值的稀疏卷积核
- Learning rate,采用cosine学习率
- Index Layer,保存每个分组卷积核最终的权重,这样在测试阶段,就不需要再经过前面分组卷积了,直接使用保存的权重编码即可。
12.2. CondenseNet V2
CVPR 2021年的论文:CondenseNet V2: Sparse Feature Reactivation for Deep Networks
官方代码:https://github.com/jianghaojun/CondenseNetV2
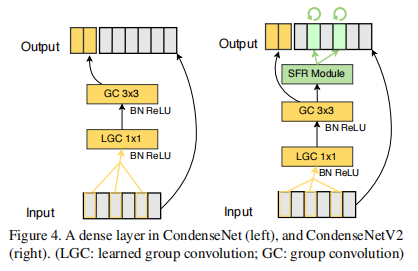
论文中认为V1中直接裁剪冗余特征过于粗暴,即使是冗余的,也有可能存在一定的信息,所以论文提出了稀疏特征重激活(Sparse feature reactivation,SFR)结构,重新利用冗余特征。对比V1的网络结构,V2的网络结构如下:
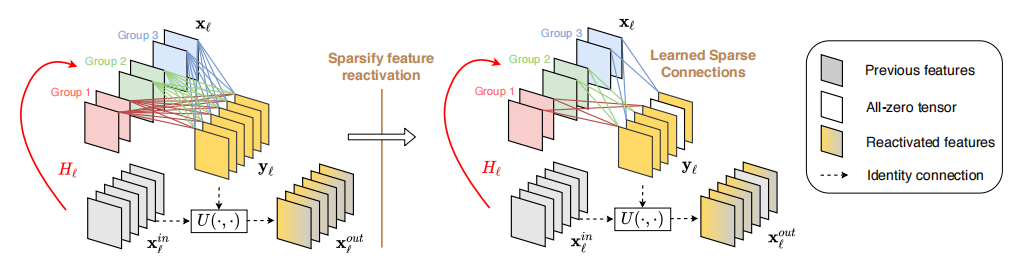
其中,SFR的结构如下:
流程伪代码(来自论文作者的论文扩展):
对比V1,V2对每个输入也做一次L1正则化,即 \(\sum_{i=1}^{I / G} |\mathbf{F}_{i, j}^{g}|\);然后根据因子 \(S\),选取权值最小的 \(O/S\) 个输出,将其置0
从论文的描述以及伪代码流程来看,是对所有的输入通道做一次筛选,怎么就是重激活了呢?但从图中来看,应该是从被丢弃的 \(I/C\) 的输入通道中做筛选,就相当于重新激活了。所以应该采用后者的做法才对。