机器学习神经网络

机器学习

发布日期: 2021-09-23

更新日期: 2024-01-24

文章字数: 3.2k

阅读时长: 12 分

阅读次数:

自编码器（Auto-Encoder，AE）和变自分编码器（Variational Auto-Encoder，VAE）是一种无监督的神经网络

1. 输入输出

训练输入： \[ X= \{x_1, x_2, ..., x_N\} \] 其中，\(x_i \in \mathbb{R}^{m},i =1,2,...,N\)，\(x_i\) 为特征域

测试输入 \[ X=\{x'_1,x'_2,...,x'_{N'}\},x'_i \in \mathbb{R}^m \] 测试输出：

用于降维类任务 \[ \hat X'=\{\hat x'_1, \hat x'_2,..., \hat x'_{N'}\},\hat x'_i \in \mathbb{R}^{m'} \]

用于生成类任务

\[ \hat X'=\{\hat x'_1, \hat x'_2,..., \hat x'_{N'}\},\hat x'_i \in \mathbb{R}^m \]

2. AE

2.1. 模型推导

原始的自编码器的结构非常简单。

原始的自编码器又称为Vanilla Autoencoder；Vanilla -> 香草 -> 冰激凌的基础口味 -> 原始的。

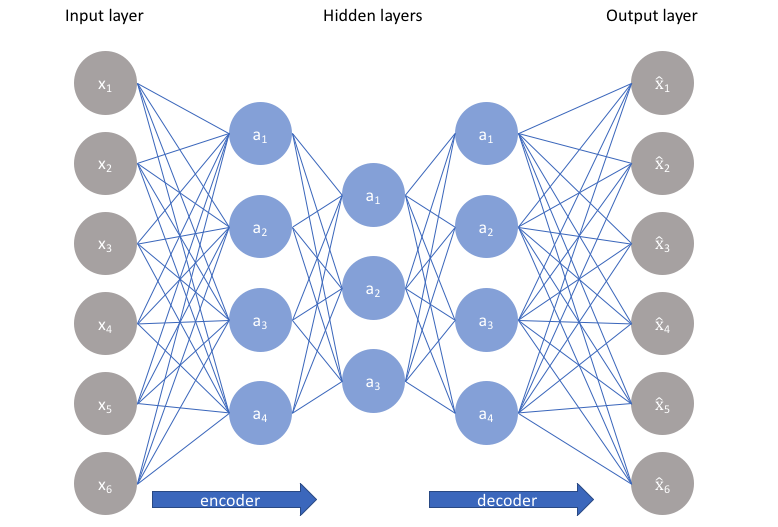
其基本思想是，输入经过一系列变换后，最终的输出和输入相同。简单来说就是输入即输出。模型的函数表达式为 \[ f(x) = x \] 一个经典的AE模型的结构如下

图中的隐藏层皆为全连接层，隐层函数表达式为 \[ h_t = a_t(W_t \cdot h_{t-1} + b_t) \] 其中，\(a(\cdot)\) 为激活函数，根据不同类型的任务选择不同的激活函数

根据每个结构的功能特点，将上述模型结构划分为两部分，一般将用于数据压缩（降维）的部分称为编码器（encoder），有时也称为识别网络；将用于参数重构（升维）的部分称为译码器（decoder），有时也称为生成网络

一般来说，都是先编码器，后译码器，但是否可以先译码器，后编码器，即先升维再降维？

网上的说法莫衷一是。

参考这个知乎的回答，从数学运算和模型功能相结合的角度进行分析。

不妨设编码器和译码器的函数表达式为 \(H = XW\) 及 \(F=HV\) ，即模型整体的表达式为 \(F=X(WV)\)，其中，\(F \approx X \in R^m, W \in R^{m \times n},V \in R^{n \times m}\)

当 \(m=n\) 时，X、H、F三者都是同秩的，所以 \(W=V=I_m\) （\(I_m\) 是秩为m的单位矩阵）必然是模型的一个最优解，即模型的参数W和V最终大概率拟合为一个单位矩阵，即网络最终大概率学习不到任何东西。

当 \(m < n\) 时，即先升维，再降维，此时存在多个解使得 \(WV=I_m\) ，即模型存在多个最优解。

当 \(m > n\) 时，即先降维，再升维，不存在解使得 \(WV = I_m\) ，因为假如存在成立解，则 \(m = r(I_m)=r(WV) \leq \min\{r(W),r(V)\} \leq \min\{n,n\}=n\) 矛盾，故不存在成立解，即模型不存在最优解。

所以对于生成类任务，是可以先升维，再降维的，而且能拟合出最优解；但对于降维类任务，先升维，再降维的做法对提取特征毫无意义，因为我们需要的是中间的特征值，当然，如果先降维，再升维，由于无法得出最优解，所以这种降维算法是有损的

损失函数一般使用L2损失，即

\[ J(x, f(x)) = ||x - f(x)||^2 \]

2.2. 一些结论

无监督类的模型都很适用于降维类或者生成类任务。

当AE用于降维类任务时，网络训练完毕后，将译码器部分去除，以编码器的输出作为模型的预测输出。

单纯的AE一般不太适用于生成类任务。因为其实质是样本空间的变换，对隐空间并没有直接约束。只考虑了可观察变量，这会带来如下问题：

容易受噪声数据干扰
对于没见过的输入，会给出意料之外的输出
以原输入再生成出原输入，在生成任务中，并未没有多大的意义。因为我们需要的是指定一些特征（例如文本），然后生成一张图片，而不是指定一张图片，再生成一张一样的图片
由于变换过程是有损的，所以是否可以生成高清原图都难以保障

当然，可以利用其容易受噪声干扰的特点，通过检测输出波动情况，可以用于异常检测任务

3. VAE

变自分编码器基于自编码器，主要用于生成类任务。

3.1. 模型推导

AE从观测变量学习的角度出发，而VAE从隐变量学习的角度出发。

一个经典的VAE框架

3.1.1. 前向传播

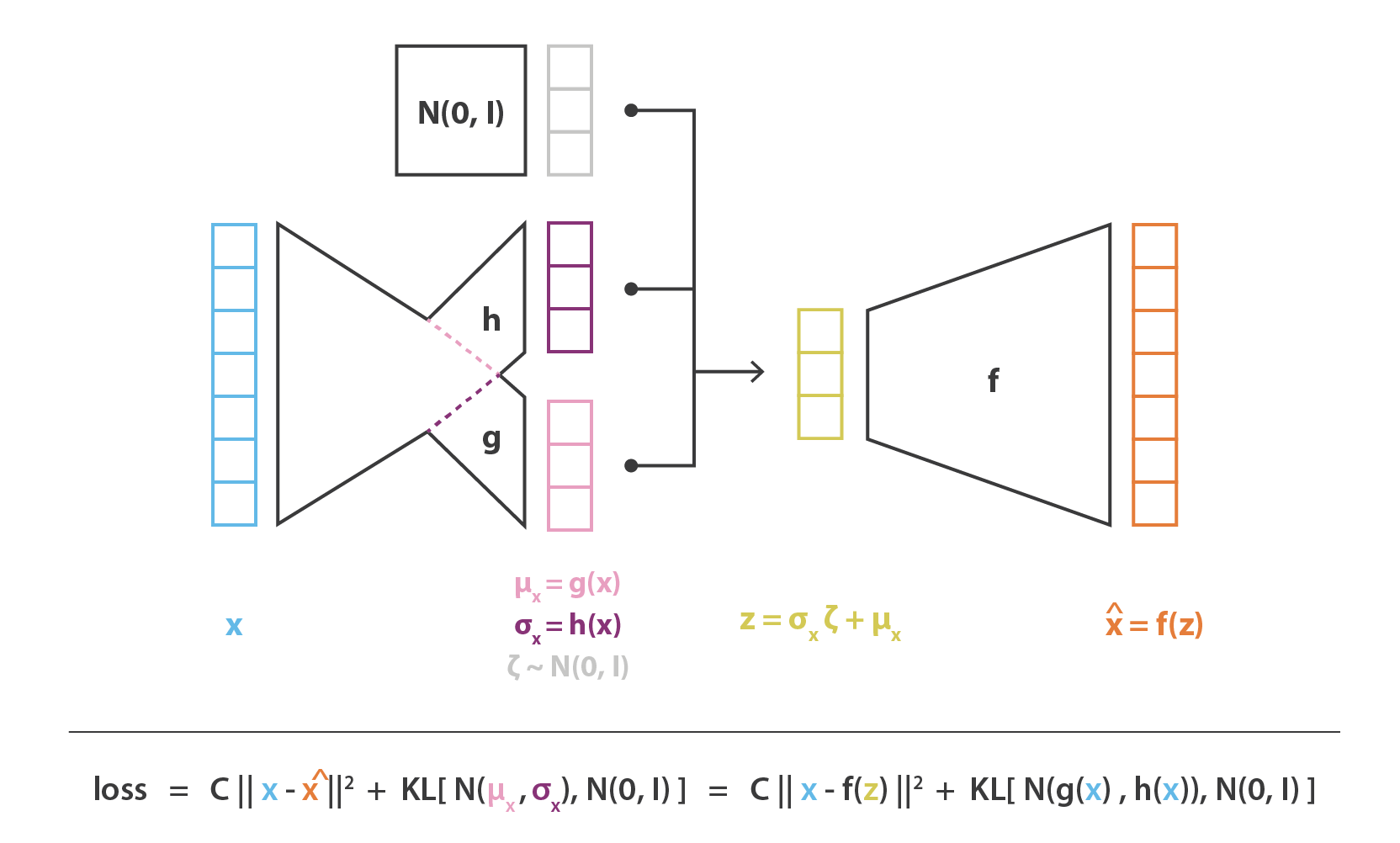
VAE结合贝叶斯理论，不再认为整个样本空间只服从一个可观测的概率分布，而认为存在一个隐变量 \(z\) ，控制着每个样本的概率分布。模型框架可以用贝叶斯公式进行概括

\[ p(z \mid x)=\frac{p(x \mid z) p(z)}{p(x)} \] 其中，\(p(x \mid z)\) 为似然性概率，表示每个隐变量的控制下生成样本的分布，具体为模型生成器的输出分布；\(p(z)\) 为先验分布，表示整个隐变量空间的分布；\(p(x)\) 为边缘概率，表示模型整体样本空间的分布；\(p(z \mid x)\) 为后验概率，表示每个样本的隐变量的分布，具体模型中编码器的输出分布

但是，上述所有概率的分布类型都是未知的，为了推导方便，不妨先假设\(p(z \mid x)\) 近似服从正态分布 \(q(z \mid x) = N(\mu, \sigma^2)\)，然后从这个假设开始进行推导。

假设为其他的分布形式也是可以的，但需要加比较严格的限定条件。

计算 \(q(z \mid x)\) 的均值 \(\mu\) 及方差 \(\sigma^2\)

由于自编码的输入即输出的特性，我们可以从每个样本输入中求取均值和方差。但直接从样本中求解均值和方差比较困难，所以直接使用两个并行的全连接层进行拟合。其中，均值计算不需要激活函数；方差计算，考虑到其非负性及后序推导的便利，对其取指数处理。两个神经层公式表示为 \[ \mu = W_\mu x + b_\mu \\ \sigma^2 = \exp(W_\sigma x+ b_\sigma) \]

原论文对方差的计算没有加激活函数，认为其输出为 \(\log \sigma^2 = W_\sigma x+ b_\sigma\)，两者是等价的，这只会影响编程上的实现。

计算 \(z \sim q(z \mid x)\)

计算出隐变量的参数 \(\mu, \sigma^2\) 后，便可以求出 \(q(z \mid x)\)，随后只需从中随机抽取一个 \(z\) 便可以生成一个样本。

随机抽取一个和随机抽取若干个进行训练的效果是一样的

所以，只需对两个全连接层的输出进行耦合，计算出分布 \(q(z \mid x) = N(\mu, \sigma^2)\) ，然后从中随机抽取一个 \(z\) ，即可完成数据流前向传递。

但是在反向传播中需要对 \(q(z \mid x)\) 进行求导，而随机抽取这一动作并不可导。论文中采用重参数技巧（reparameterization trick）解决这一问题。

基于前面的假设，我们有 \[ \begin{aligned} & E_{z \sim N(\mu, \sigma^2)}[f(z)] \\=&\int \frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{(z-\mu)^{2}}{2 \sigma^{2}}\right) d z \\=&\int \frac{1}{\sqrt{2 \pi}} \exp \left[-\frac{1}{2}\left(\frac{z-\mu}{\sigma}\right)^{2}\right] d\left(\frac{z-\mu}{\sigma}\right) \\ =&\int \frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{\epsilon^2}{2}\right) d\epsilon \\=& E_{\epsilon \sim N(0,I)}\left [f(\epsilon) \right ] \end{aligned} \] 其中，\(\epsilon = \frac{z-\mu}{\sigma}\)，转换可得 \(z=\mu+\epsilon \sigma\)

在 \(N(\mu, \sigma^2)\) 中采样一个 \(z\)，等价于从 \(N(0,I)\) 中采样一个 \(\epsilon\)，然后做变换 \(\mu+\epsilon \sigma\) 得到 \(z\)，所以只需将 \(p(z)\) 近似服从标准正态分布 \(N(0,I)\) ，即可将上述转换代入前向传播的过程中，此时两个全连接层的耦合表达式为

\[ z=\mu+\epsilon \sigma \] 而后续的反向传播过程中，由于 \(p(z)\) 是先验分布，并不需要对 \(p(z)\) 进行拟合，而 \(\epsilon\) 又将作为一个权重参数参与求导计算，从而绕开了对随机抽取动作求导，非常的巧妙。

计算 \(\hat x\)

令 \(\hat x = p(x \mid z)\)，不知道具体的概率分布，也直接使用一个全连接层拟合即可：

\[ \hat x = W_z z + b_z \]

3.1.2. 反向传播

根据经典的贝叶斯推断，使后验分布假设 \(q(z \mid x)\) 近似于 \(p(z \mid x)\)，使用变分推断进行推导。目标函数表示为 \[ \begin{aligned} J =& \text{KL}\left(q(z \mid x) \| p(z \mid x)\right) \\=& E_{z \sim q(x)}[\log p(x \mid z)] + \text{KL} (q(z \mid x) || p(z)) \\ =& L + \Phi \end{aligned} \]

变分推断相关知识可以参考这篇笔记：数学工具-变分推断

另外，个人感觉如果仅因为采用了KL散度就称该模型为变分编码器，有点过于简单粗暴。由于该模型实际上更多应用的是贝叶斯推断，所以该模型更偏向于被称为贝叶斯自编码器

函数由两部分组成，第一项是模型的损失函数，第二项是正则项。

第一项由正态分布的定义可得 \[ E_{z \sim q(x)}[\log p(x \mid z)] = E_{z \sim q(x)}\left(\frac{\|x-f(z)\|^{2}}{2 \sigma^2}\right) \] 第二项可以理解为对隐空间的约束。由于 \(p(z) = N(0,I)\)，使 \(q(z \mid x)\) 近似于 \(p(z)\)，即其使 \(q(z \mid x)\) 的均值趋向于0，且方差趋向于1，使模型中存在噪声，提高模型的泛化能力，否则模型就会退化成一般的自编码。其推导为 \[ \begin{aligned} &\text{KL} (q(z \mid x) || p(z)) \\ =& \text{KL}\left(N\left(\mu, \sigma^{2}\right) \| N(0,1)\right) \\=& \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-(x-\mu)^{2} / 2 \sigma^{2}}\left(\log \frac{e^{-(x-\mu)^{2} / 2 \sigma^{2}} / \sqrt{2 \pi \sigma^{2}}}{e^{-x^{2} / 2 / \sqrt{2 \pi}}}\right) d x \\=& \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-(x-\mu)^{2} / 2 \sigma^{2}} \log \left\{\frac{1}{\sqrt{\sigma^{2}}} \exp \left\{\frac{1}{2}\left[x^{2}-(x-\mu)^{2} / \sigma^{2}\right]\right\}\right\} d x \\=& \frac{1}{2} \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-(x-\mu)^{2} / 2 \sigma^{2}}\left[-\log \sigma^{2}+x^{2}-(x-\mu)^{2} / \sigma^{2}\right] d x \\=& \frac{1}{2}\left(-\log \sigma^{2}+\mu^{2}+\sigma^{2}-1\right) \end{aligned} \]

3.2. 实际应用

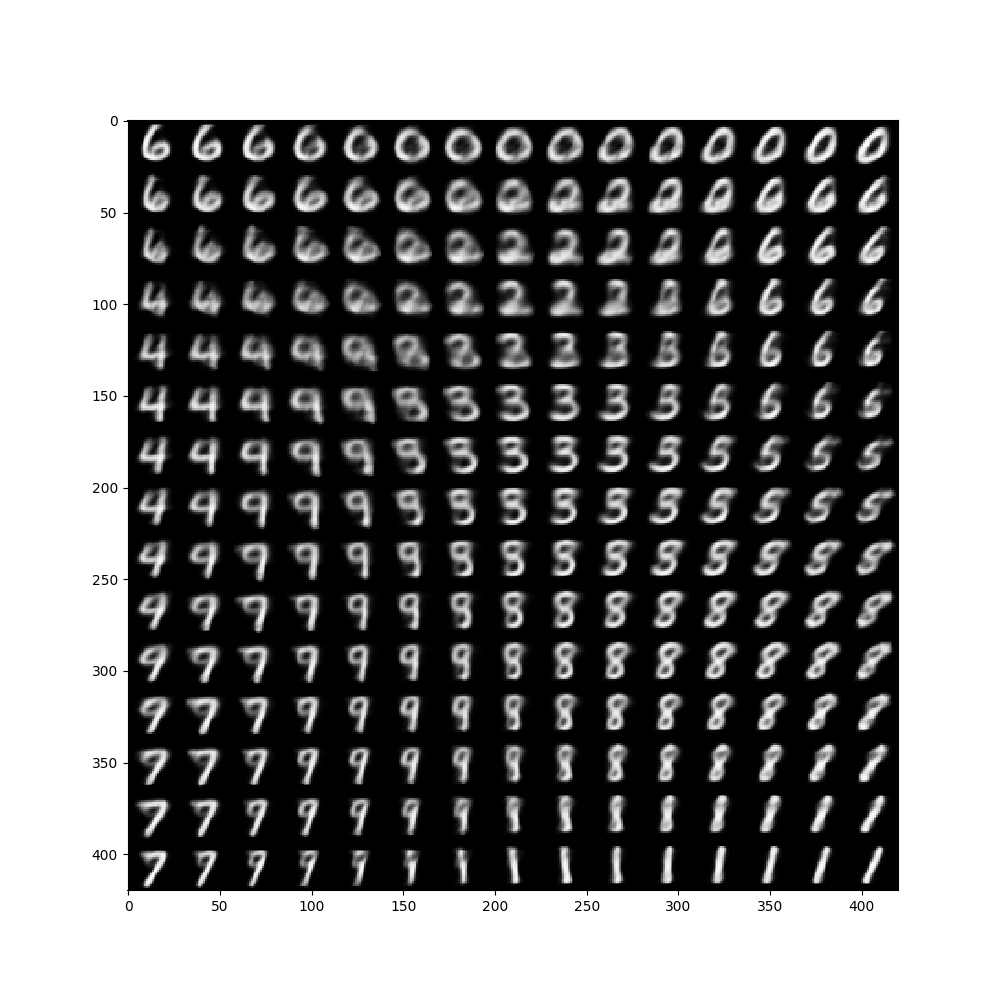
应用于实际的生成任务时，只保留生成器。每次从多元标准正态分布中随机抽取一个点，即可生成一个图像。

这是一个使用手写数据集作为训练集的生成任务demo。为方便作图，使 \(z\) 服从二元标准正态分布。下图是进行从二元标准正态分布抽取若干个点生成的若干个图像。

4. 相关研究工作

正则自编码（Regularized AE）
- 稀疏自编码器（Sparse AE）
  
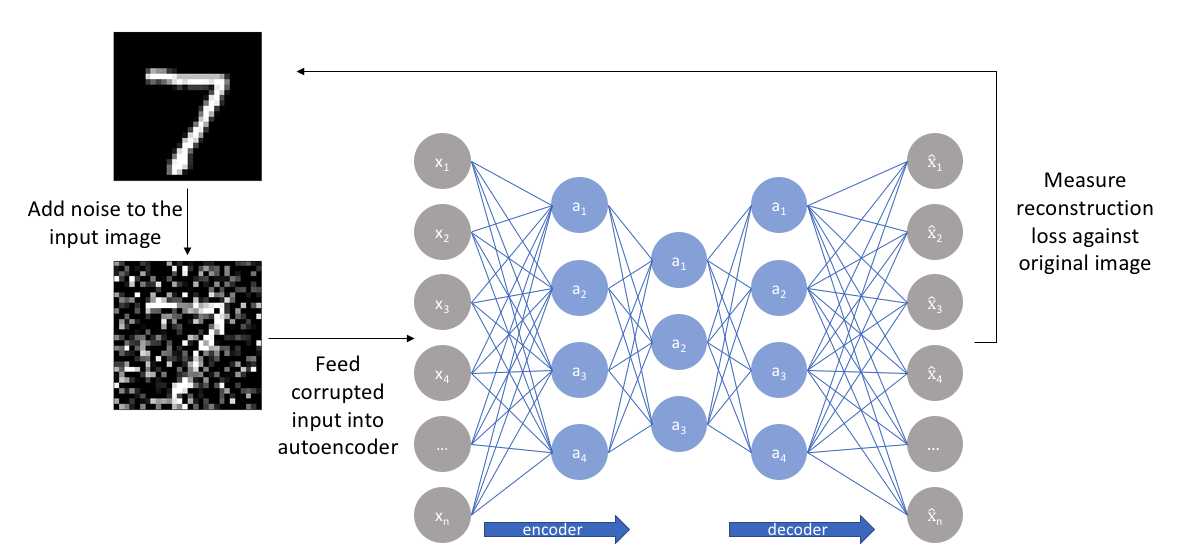
  论文：Sparse autoencoder, Andrew Ng, etc, 2011
- 降噪自编码器（Denoising AE）
收缩自编码器（Contractive AE）
浅层自编码器（Shallow AE）

编码器和解码器中只有一个层。它与 PCA 的区别是在编码器中使用 ReLU 激活函数，在解码器中使用 sigmoid 函数，因此它是非线性的。
堆叠自编码器（Stacked AE）

训练方式不是端到端，而是逐层贪婪训练。

论文：Stacked Convolutional Auto-Encoders for Hierarchical Feature, Jonathan Masci, Jurgen Schmidhuber etc, 2011
Beta 变分自编码器（beta-VAE）

对vae的改进，反向传播时，对正则项加入影响因子 \(\beta\) ，用以加深/减轻对隐空间的约束。
向量量化变分自编码器（vq-VAE）

对vae的改进，使用均匀的类别分布抽取替代随机抽样
多层自编码器（Multilayer AE）
卷积自编码器（Convolutional AE）

使用卷积层作为隐层