1. 基本定义

对于未知且形式难以给出的分布 \(p(z)\)，MCMC采取模拟取样的方法进行近似。但对于大量数据，MCMC的计算较慢。而变分推断的基本思想是，直接构造一个容易观察的分布 \(q(z)\) ，不断缩短两个分布的距离，直到收敛。此时， \(q(z)\) 就可以看做是 \(p(z)\) 的近似。其中，\(q(z)\) 也称为变分分布（variational distribution）

假设\(x\)是观测变量，\(z\)是隐变量，\(\theta\) 是参数。由于在贝叶斯推断中，对隐变量的推断都转化为后验概率计算，所以变分推断中，\(q(z)\) 一般不直接近似先验分布 \(p(z)\)，而是近似后验概率 \(p(z|x)\)

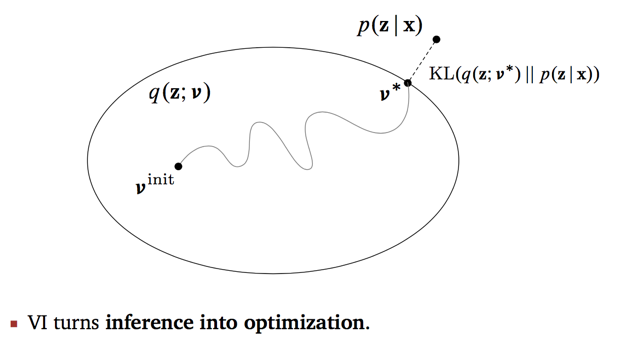
两分布间距离一般使用KL散度\(\text{KL}(q(z)‖p(z|x))\) 进行定义，该值越小，两个分布越接近。所以变分推断的目标是 \(q(z^*)=\arg \min_{q(z) \in Q} \text{KL}(q(z)‖p(z|x))\)，如下图所示

上图中，\(v\) 是关于 \(q\) 的未知参数，又由于在进行一般推导时，假设 \(v\) 只与 \(q\) 有关，所以 \(q(z;v)\) 一般也简写为 \(q(z)\)。

另外，一般假设 \(q(z)\) 中所有分量是互相独立的，此时的变分分布又称为平均场（mean field）。

2. 具体方法

对两分布的KL散度进行展开 \[ \begin{aligned} \text{KL}(q(z) \| p(z \mid x)) &=E_{q}[\log q(z)]-E_{q}[\log p(z \mid x)] \\ &=E_{q}[\log q(z)]-E_{q}[\log p(x, z)]+\log p(x) \\ &=\log p(x)-\left\{E_{q}[\log p(x, z)]-E_{q}[\log q(z)]\right\} \end{aligned} \] 其中，\(E_q[\cdot]\) 表示期望是对于分布 \(q\) 上的期望，先验分布 \(p(x) = \int p(x,z)dz\) 是一个常量（这里以连续型数据为例，离散型数据改为求和即可）

KL散度取值大于等于0，于是上式可以改写为 \[ \log p(x) \geq E_q[\log p(x,z)] - E_q[\log q(z)] = L(q) \] 其中，左端称作证据（evidence），右端称为证据下界（evidence lower bound, ELBO）

当且仅当两个分布一致时，KL散度的值为0，又由于 \(\log p(x)\) 是一个常量，所以原问题转换为求解右边证据下界 \(L(q)\) 的最大值

所以目标函数可以直接定义为 \(L(q)\)

\[ \begin{aligned} J= L(q) &= E_q[\log p(x,z)] - E_q[\log q(z)] \\ & = E_q[\log p(z)] + E_q[\log p(x|z)] - E_q[\log q(z)] \\ &= E_q[\log p(x|z)] - \text{KL} (q(z) || p(z)) \end{aligned} \] 其中，