1. 模型推导

1.1. 基本定义

首先先给出如下定义

单词集合 $W=\{w_1,\cdots,w_v,\cdots,w_V\}$，V是单词的个数
文本集合 $D=\{\mathbf w_1,\cdots,\mathbf w_m,\cdots,\mathbf w_M\}$，M是文本的个数，其中，文本 $\mathbf w_m$ 是一个单词序列 $w_m=(\mathbf w_{m1},\cdots,\mathbf w_{mn},\cdots,\mathbf w_{mN_m})$，$N_m$ 是文本 $\mathbf w_m$ 的单词的个数
话题集合 $Z = \{z_1,\cdots,z_k,\cdots,z_K\}$，K是话题的个数
每个话题 $z_k$ 由条件概率分布 $p(w|z_k)$ 决定。分布 $p(w|z_k)$ 服从多项式分布，其参数为 $\varphi_k=(\varphi_{k1},\cdots,\varphi_{kV})$，$\varphi_k$ 表示话题 $z_k$ 生成单词 $w_v$ 的概率。参数 $\varphi_k$ 的先验输入服从狄利克雷分布，其超参数为 $\beta=(\beta_1,\cdots,\beta_V)$
每个文本 $\mathbf w_m$ 由一个话题的条件概率分布 $p(z|\mathbf w_m)$ 决定。分布 $p(z|\mathbf w_m)$ 服从多项分布，其参数为 $\theta_m=(\theta_{m1},\cdots,\theta_{mK})$ ，表示文本 $\mathbf w_m$ 生成话题 $z_k$ 的概率。参数 $\theta_m$ 的先验输入服从狄利克雷分布，其超参数为 $\alpha=(\alpha_1,\cdots,\alpha_K)$ 。

1.2. 学习策略

LDA算法的生成过程和PLSA算法的生成模型的生成过程类似，其最大区别是LDA提供了先验分布作为参考，而PLSA没有。更具体的，PLSA的生成过程简述为 $d \rightarrow z \rightarrow w$，而LDA的生成过程简述为 $\theta \rightarrow z \rightarrow w \leftarrow \varphi$

LDA的具体流程如下：

生成文本的话题分布。按照狄利克雷分布 $\operatorname{Dir}(\alpha)$ 随机生成一个参数向量 $\theta_m$，循环$M$遍，得到参数向量 $\theta = (\theta_1,\cdots,\theta_M)$
生成话题。取第m个文本的参数 $\theta_m$，按照多项分布$\operatorname{Mult}(\theta_m)$随机生成一个话题 $z_{mn}$，循环 $N_m$ 遍，得到话题向量 $z_m=(z_{m1},\cdots,z_{mN_m})$
生成话题的单词分布。按照狄利克雷分布 $\operatorname{Dir}(\beta)$ 随机生成一个参数向量 $\varphi_k$，循环$K$遍，得到参数向量 $\varphi_1,\cdots,\varphi_K$
生成单词。取第m个文本的第n个话题的参数 $\varphi_{z_{mn}}$，按照多项分布$\operatorname{Mult}(\varphi_{z_{mn}})$随机生成一个单词 $w_{mn}$，循环 $N_m$ 遍，得到单词序列 $w_m=(w_1,\cdots,w_{mN_m})$，其对应话题序列 $z_m$

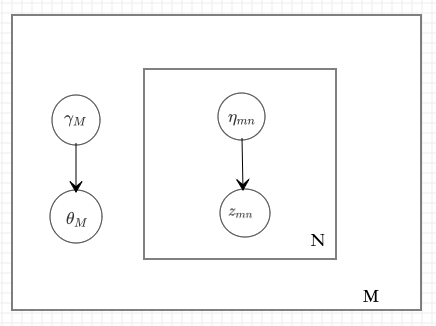
概率图表示如下

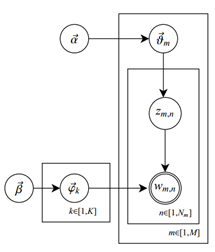
由上面概率图可得LDA模型的联合概率表示形式：

\[ p(\mathbf{w}, \boldsymbol{z}, \theta, \varphi \mid \alpha, \beta)=\prod_{k=1}^{K} p\left(\varphi_{k} \mid \beta\right) \prod_{m=1}^{M} p\left(\theta_{m} \mid \alpha\right) \prod_{n=1}^{N_{m}} p\left(z_{m n} \mid \theta_{m}\right) p\left(w_{m n} \mid z_{m n}, \varphi\right) \]

其中，$\mathbf{w}$ 为观测变量，$\boldsymbol{z}, \theta, \varphi$ 是隐变量

更进一步的，第 $m$ 个文本的联合概率可以表示为 \[ p(\mathbf{w}_m, \boldsymbol{z}_m, \theta_m, \varphi \mid \alpha, \beta)=\prod_{k=1}^{K} p\left(\varphi_{k} \mid \beta\right) p\left(\theta_{m} \mid \alpha\right) \prod_{n=1}^{N_{m}} p\left(z_{m n} \mid \theta_{m}\right) p\left(w_{m n} \mid z_{m n}, \varphi\right) \] 对隐变量进行积分得到边缘分布，参数 $\theta_m, \varphi$ 给定的情况下，第$m$个文本的生成概率是： \[ p\left(\mathbf{w}_{m} \mid \theta_{m}, \varphi\right)=\prod_{n=1}^{N_{m}}\left[\sum_{k=1}^{K} p\left(z_{m n}=k \mid \theta_{m}\right) p\left(w_{m n} \mid \varphi_{k}\right)\right] \] 超参数 $\alpha, \beta$ 给定的条件下，第$m$个文本的生成概率是： \[ p(\mathbf{w}_m \mid \alpha, \beta)=\prod_{k=1}^{K} \int p\left(\varphi_{k} \mid \beta\right)\left\{ \int p\left(\theta_{m} \mid \alpha\right) \prod_{n=1}^{N_{m}}\left[\sum_{l=1}^{K} p\left(z_{m n}=l \mid \theta_{m}\right) p\left(w_{m n} \mid \varphi_{l}\right)\right] \mathbf d \theta_{m}\right\} \mathbf d \varphi_{k} \] 推出所有文本的生成概率是 \[ p(\mathbf{w} \mid \alpha, \beta)=\prod_{k=1}^{K} p(\mathbf{w}_m \mid \alpha, \beta) \]

1.3. 学习算法

在LDA这个估计主题分布、词分布的过程中，它们的先验分布（即Dirichlet分布）事先由人为给定，所以最终问题只需要计算其后验概率分布即可。后验分布的计算涉及到未知参数 $\theta$ 和 $\varphi$，而潜在狄利克雷分布的学习（参数估计）是一个复杂的最优化问题，很难精确求解，只能近似求解。

常用的近似求解方法有吉布斯抽样（MCMC）和变分EM算法（变分推理）。MCMC通过随机抽样的方法近似的计算模型的后验概率；变分推理则通过解析的方法计算模型的后验概率的近似值。

1.3.1. 吉布斯抽样

吉布斯抽样的具体推导可以参考笔记：数学工具-MCMC

1.3.1.1. 基本想法

LDA通过对后验概率 $p(z|\mathbf w)$ 的积分计算对参数进行估计

通过对观测到的变量积分计算得到参数的方法称为collapsed，所以此时的吉布斯抽样也叫收缩的吉布斯抽样（collapsed Gibbs sampling）算法

1.3.1.2. 算法推导

对后验概率进行简化 \[ p(z|\mathbf w,\alpha,\beta) = \frac{p(z,\mathbf w|\alpha,\beta)}{p(\mathbf w|\alpha,\beta)} \propto p(z,\mathbf w|\alpha,\beta) \] 上式中，分母是观测变量的边际概率，与其他的概率图模型一样的，或者由前面的推导可知，其计算量非常大，吉布斯抽样的好处就是可以通过对后验概率 $p(z,\mathbf w|\alpha,\beta)$ 抽样近似计算 $p(z|\mathbf w,\alpha,\beta)$

下面对 $p(\mathbf{w} \mid z, \beta)$ 进行推导，$p(z\mid\alpha)$ 的推导如法炮制即可

设$n_{kv}$ 为第 $k$ 个话题生成第 $v$ 个单词的次数，$\varphi_{kv}$ 表示第 $k$ 个话题生成第 $v$ 个单词的概率；由于LDA是词袋模型，其假设词与词之间是独立分布的，故

生成 $K$ 个服从多项分布 $\mathbf w \sim \text{Mult}(n,\varphi)$ 的单词的概率为 \[ p(\mathbf{w} \mid z, \varphi) = \prod_{k=1}^{K} \prod_{v=1}^{V} \varphi_{k v}^{n_{kv}} \] 生成 $K \times V$ 个服从 $\varphi \sim \text{Dir}(\beta)$ 的分布的概率为 \[ p(\varphi \mid \beta) = \prod_{k=1}^{K} \frac{1}{B(\alpha)} \prod_{v=1}^{V} \varphi_{k v}^{\beta_{v}-1} \] 又目标分布 $p(\mathbf{w} \mid z, \beta)$ 需要对词分布 $\varphi$ 进行积分，得 \[ \begin{aligned} p(\mathbf{w} \mid z, \beta) &=\int p(\mathbf{w} \mid z, \varphi) p(\varphi \mid \beta) \mathbf d \varphi \\ &=\int \prod_{k=1}^{K} \frac{1}{B(\beta)} \prod_{v=1}^{V} \varphi_{k v}^{n_{kv}+\beta_{v}-1} \mathbf d \varphi \\ &=\prod_{k=1}^{K} \frac{B\left(n_{k}+\beta\right)}{B(\beta)} \end{aligned} \] 同理，可得

\[ \begin{aligned} p(z \mid \alpha) &=\int p(z \mid \theta) p(\theta \mid \alpha) \mathbf d \theta \\ &=\int \prod_{m=1}^{M} \frac{1}{B(\alpha)} \prod_{k=1}^{K} \theta_{m k}^{n_{m k}+\alpha_{k}-1} \mathbf d \theta \\ &=\prod_{m=1}^{M} \frac{1}{B(\alpha)} \int \prod_{k=1}^{K} \theta_{m k}^{n_{m k}+\alpha_{k}-1} \mathbf d \theta \\ &=\prod_{m=1}^{M} \frac{B\left(n_{m}+\alpha\right)}{B(\alpha)} \end{aligned} \]

于是，得 \[ p(z|\mathbf w,\alpha,\beta) \propto p(\mathbf w,z|\alpha,\beta) = \prod_{k=1}^{K} \frac{B\left(n_{k}+\beta\right)}{B(\beta)} \cdot \prod_{m=1}^{M} \frac{B\left(n_{m}+\alpha\right)}{B(\alpha)} \] 接着计算 $p(z|w,,) $ 的满条件分布形式 \[ \begin{aligned} p\left(z_{i} \mid z_{-i}, \mathbf {w}, \alpha, \beta\right) &= \frac{p(\mathbf w, z \mid \alpha, \beta)}{p(\mathbf w, z_{-i} \mid \alpha, \beta)} \\ & \propto \frac{1}{p(\mathbf w_{-i}, z_{-i} \mid \alpha, \beta)} \\ &= \frac{n_{k v}+\beta_{v}}{\sum_{v=1}^{V}\left(n_{k v}+\beta_{v}\right)} \cdot \frac{n_{m k}+\alpha_{k}}{\sum_{k=1}^{K}\left(n_{m k}+\alpha_{k}\right)} \end{aligned} \] 又因为 \[ \begin{aligned} p\left(z_{i} \mid z_{-i}, \mathbf {w}, \alpha, \beta\right) & \propto p\left(z_{i}, \mathbf {w}_i \mid z_{-i}, \mathbf {w}_{-i}, \alpha, \beta\right) \\ &= \int p\left(z_{i}, \mathbf {w}_i ,\theta_m, \varphi_k \mid z_{-i}, \mathbf {w}_{-i}, \alpha, \beta\right) \mathbf d \theta_m \mathbf d \varphi_k \\ &= \int p\left(z_{i}, \theta_m, \mid z_{-i}, \mathbf {w}_{-i}, \alpha\right) \cdot p\left(\mathbf {w}_i ,\varphi_k \mid z_{-i}, \mathbf {w}_{-i}, \beta\right) \mathbf d \theta_m \mathbf d \varphi_k \\ &= \int p(z_i \mid \theta_m, \alpha)\cdot p(\theta_m \mid z_{-i}, \mathbf {w}_{-i}, \alpha) \cdot p(\mathbf w_i \mid \varphi_k, \beta)\cdot p(\varphi_k \mid z_{-i}, \mathbf {w}_{-i}, \beta) \mathbf d \theta_m \mathbf d \varphi_k \\ &= \int \theta_{mk} \text{Dir}(\theta_m\mid n_{m,-i}+\alpha) \mathbf d \theta_m \cdot \int \varphi_{kv} \text{Dir}(\varphi_k\mid n_{k,-i}+\beta) \mathbf d \varphi_k \\ &= E(\theta_{mk}) \cdot E(\varphi_{kv}) \\&= \hat{\theta}_{mk} \cdot \hat{\varphi}_{kv} \end{aligned} \] 故， $\theta$ 和 $\varphi$ 的参数估计的计算公式为 \[ \begin{aligned} \theta_{m k} &=\frac{n_{m k}+\alpha_{k}}{\sum_{k=1}^{K}\left(n_{m k}+\alpha_{k}\right)} \\ \varphi_{k v} &=\frac{n_{k v}+\beta_{v}}{\sum_{v=1}^{V}\left(n_{k v}+\beta_{v}\right)} \end{aligned} \]

1.3.2. 变分EM算法

变分推断的具体推导可以参考笔记：数学工具-变分推断

1.3.2.1. 基本想法

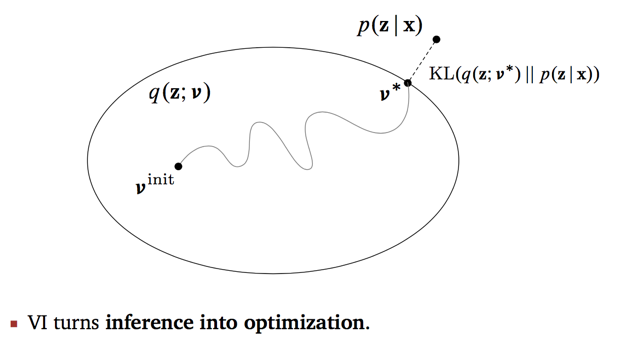
假设一个便于观测的分布 $q(z)$，使用变分推断给出证据下界，采用EM算法迭代求解最大化，使其近似模型后验分布 $p(z|x)$。

可以证明变分EM算法一定收敛，但可能收敛到局部最优

下面将变分EM算法应用至简化版的LDA模型中，当然也可以应用于正常的LDA模型中，结果是等价的。

简化版的LDA模型将参数 $\beta$ 与 $\varphi$ 看做一个整体，将 $\alpha,\varphi$ 看做未知参数，模型的联合分布也变为 \[ p(\theta,z,\mathbf w \mid \alpha, \varphi) = p(\theta \mid \alpha) \prod_{n=1}^N p(z_n \mid \theta) p(w_n \mid z_n, \varphi) \] 于是，算法的思路为，从后验概率分布 $p(\theta,z \mid \mathbf{w}, \alpha, \varphi)$ 入手对参数$\alpha,\varphi$ 进行估计

不妨假设变分分布的概率表示为

其中，$\gamma,\eta$ 是变分分布的参数

如果 $\theta,z$ 的各个分量都是独立的，则平均场分布表示为 \[ q(\theta,z \mid \gamma , \eta) = q(\theta\mid \gamma \prod_{n=1}^N q(z_n \mid \eta_n)) \] 用上述分布近似后验概率分布 $p(\theta,z \mid \mathbf{w}, \alpha, \varphi)$

1.3.2.2. 算法推导

首先写出变分分布的证据下界 \[ \begin{aligned} L(\gamma, \eta, \alpha, \varphi) &=E_{q}[\log p(\theta, z, \mathbf w \mid \alpha, \varphi)]-E_{q}[\log q(\theta, z \mid \gamma, \eta)] \\ &=E_{q}[\log p(\theta \mid \alpha)]+E_{q}[\log p(z \mid \theta)]+E_{q}[\log p(\mathbf w \mid z, \varphi)] \\ &\quad -E_{q}[\log q(\theta \mid \gamma)] -E_{q}[\log q[z \mid \eta]] \end{aligned} \] 对上面式子中的5项分别单独进行推导

第一项， \[ E_{q}[\log p(\theta \mid \alpha)]=\sum_{k=1}^{K}\left(\alpha_{k}-1\right) E_{q}\left[\log \theta_{k}\right]+\log \Gamma\left(\sum_{l=1}^{K} \alpha_{l}\right)-\sum_{k=1}^{K} \log \Gamma\left(\alpha_{k}\right) \] 其中，$\theta \sim \text{Dir}(\theta \mid \gamma)$，可得 \[ E_{q(\theta \mid \gamma)}\left[\log \theta_{k}\right]=\Psi\left(\gamma_{k}\right)-\Psi\left(\sum_{l=1}^{K} \gamma_{l}\right) \] 最终得 \[ E_{q}[\log p(\theta \mid \alpha)]=\log \Gamma\left(\sum_{l=1}^{K} \alpha_{l}\right)-\sum_{k=1}^{K} \log \Gamma\left(\alpha_{k}\right)+\sum_{k=1}^{K}\left(\alpha_{k}-1\right)\left[\Psi\left(\gamma_{k}\right)-\Psi\left(\sum_{l=1}^{K} \gamma_{l}\right)\right] \]
第二项， \[ \begin{aligned} E_{q}[\log p(z \mid \theta)] &=\sum_{n=1}^{N} E_{q}\left[\log p\left(z_{n} \mid \theta\right)\right] \\ &=\sum_{n=1}^{N} E_{q\left(\theta, z_{n} \mid \gamma, \eta\right)}\left[\log \left(z_{n} \mid \theta\right)\right] \\ &=\sum_{n=1}^{N} \sum_{k=1}^{K} q\left(z_{n k} \mid \eta\right) E_{q(\theta \mid \gamma)}\left[\log \theta_{k}\right] \\ &=\sum_{n=1}^{N} \sum_{k=1}^{K} \eta_{n k}\left[\Psi\left(\gamma_{k}\right)-\Psi\left(\sum_{l=1}^{K} \gamma_{l}\right)\right] \end{aligned} \]
第三项， \[ \begin{aligned} E_{q}[\log p(\mathbf w \mid z, \varphi)] &=\sum_{n=1}^{N} E_{q}\left[\log p\left(w_{n} \mid z_{n}, \varphi\right)\right] \\ &=\sum_{n=1}^{N} E_{q\left(z_{n} \mid \eta\right)}\left[\log p\left(w_{n} \mid z_{n}, \varphi\right)\right] \\ &=\sum_{n=1}^{N} \sum_{k=1}^{K} q\left(z_{n k} \mid \eta\right) \log p\left(w_{n} \mid z_{n}, \varphi\right) \\ &=\sum_{n=1}^{N} \sum_{k=1}^{K} \sum_{v=1}^{V} \eta_{n k} w_{n}^{v} \log \varphi_{k v} \end{aligned} \]
第四项， \[ E_{q}[\log q(\theta \mid \gamma)]=\log \Gamma\left(\sum_{l=1}^{K} \gamma_{l}\right)-\sum_{k=1}^{K} \log \Gamma\left(\gamma_{k}\right)+\sum_{k=1}^{K}\left(\gamma_{k}-1\right)\left[\Psi\left(\gamma_{k}\right)-\Psi\left(\sum_{l=1}^{K} \gamma_{l}\right)\right] \]
第五项， \[ \begin{aligned} E_{q}[\log q[z \mid \eta]] &=\sum_{n=1}^{N} E_{q}\left[\log q\left[z_{n} \mid \eta\right]\right] \\ &=\sum_{n=1}^{N} E_{q\left(z_{n} \mid \eta\right)}\left[\log q\left[z_{n} \mid \eta\right]\right] \\ &=\sum_{n=1}^{N} \sum_{k=1}^{K} E_{q(z n \downarrow \eta)}\left[\log q\left[z_{n k} \mid \eta\right]\right] \\ &=\sum_{n=1}^{N} \sum_{k=1}^{K} \eta_{n k} \log \eta_{n k} \end{aligned} \]

接下来就是EM算法

E step

固定模型参数 $\alpha,\varphi$，计算变分参数 $\gamma,\eta$

注意到，参数 $\eta$ 为话题生成单词的概率，满足 $\sum_{l=1}^K \eta_{nl}=1$

分别提取包含 $\gamma,\eta$ 的项，分别构建约束最优化问题的拉格朗日函数 \[ L_{\left[\eta_{n k}\right]}=\eta_{n k}\left[\Psi\left(\gamma_{k}\right)-\Psi\left(\sum_{k=1}^{K} \gamma_{l}\right)\right]+\eta_{n k} \log \varphi_{k v}-\eta_{n k} \log \eta_{n k}+\lambda_{n}\left(\sum_{l=1}^{K} \eta_{n l}-1\right) \]

\[ \begin{aligned} L_{\left[\gamma_{k}\right]}=& \sum_{k=1}^{K}\left(\alpha_{k}-1\right)\left[\Psi\left(\gamma_{k}\right)-\Psi\left(\sum_{l=1}^{K} \gamma_{l}\right)\right]+\sum_{n=1}^{N} \sum_{k=1}^{K} \eta_{n k}\left[\Psi\left(\gamma_{k}\right)-\Psi\left(\sum_{l=1}^{K} \gamma_{l}\right)\right]-\\ & \log \Gamma\left(\sum_{l=1}^{K} \gamma_{l}\right)+\log \Gamma\left(\gamma_{k}\right)-\sum_{k=1}^{K}\left(\gamma_{k}-1\right)\left[\Psi\left(\gamma_{k}\right)-\Psi\left(\sum_{l=1}^{K} \gamma_{l}\right)\right] \end{aligned} \]

分别求偏导并令其为0 \[ \frac{\partial L}{\partial \eta_{n k}}=\Psi\left(\gamma_{k}\right)-\Psi\left(\sum_{l=1}^{K} \gamma_{l}\right)+\log \varphi_{k v}-\log \eta_{n k}-1+\lambda_{n} \]

\[ \frac{\partial L}{\partial \gamma_{k}}=\left[\Psi^{\prime}\left(\gamma_{k}\right)-\Psi^{\prime}\left(\sum_{l=1}^{K} \gamma_{l}\right)\right]\left(\alpha_{k}+\sum_{n=1}^{N} \eta_{n k}-\gamma_{k}\right) \]

解得各参数的估计值 \[ \eta_{n k} \propto \varphi_{k v} \exp \left[\varphi\left(\gamma_{k}\right)-\varphi\left(\sum_{l=1}^{K} \gamma_{l}\right)\right] \]

\[ \gamma_{k}=\alpha_{k}+\sum_{n=1}^{N} \eta_{n k} \]

整理为算法流程如下：

Init: $\eta_{nk}^{(0)}=1/K,\gamma_k=\alpha_k + N/K$

Repeat:

for n in 1 to N:
- for k in 1 to K:
  
  $\eta_{n k}^{(t+1)}=\varphi_{k v} \exp \left[\varphi\left(\gamma_{k}^{(t)}\right)-\varphi\left(\sum_{l=1}^{K} \gamma_{l}^{(t)}\right)\right]$
  
  规范化 $\eta_{n k}^{(t+1)}$ 使其和为1
- $\gamma^{(t+1)}=\alpha+\sum_{n=1}^{N} \eta_{n}^{(t+1)}$

Until: 收敛

M step

固定变分参数 $\gamma,\eta$，计算模型参数 $\alpha,\varphi$

注意到，参数 $\eta$ 为话题生成单词的概率，满足 $\sum_{l=1}^K \eta_{nl}=1$

分别提取包含 $\beta,\alpha$ 的项，分别构建约束最优化问题的拉格朗日函数

这里，由于 $\beta$ 项仅包含一个分量，所以按照上面方法求解即可

首先写出对应的拉格朗日函数 \[ L_{[\beta]}=\sum_{m=1}^{M} \sum_{n=1}^{N_{m}} \sum_{k=1}^{K} \sum_{v=1}^{V} \eta_{m n k} w_{m n}^{v} \log \varphi_{k v}+\sum_{k=1}^{K} \lambda_{k}\left(\sum_{v=1}^{V} \varphi_{k v}-1\right) \]

求偏导并令其为0，解得参数的估计值 \[ \varphi_{k v}=\sum_{m=1}^{m} \sum_{n=1}^{N_{m}} \eta_{m n k} w_{m n}^{v} \] 而 $\alpha$ 涉及两个分量 $\alpha_k,\alpha_l$，所以得分步求解

首先写出对应的拉格朗日函数 \[ L_{[\alpha]}=\sum_{m=1}^{M}\left\{\log \Gamma\left(\sum_{l=1}^{K} \alpha_{l}\right)-\sum_{k=1}^{K} \log \Gamma\left(\alpha_{k}\right)+\sum_{k=1}^{K}\left(\alpha_{k}-1\right)\left[\Psi\left(\gamma_{m k}\right)-\Psi\left(\sum_{l=1}^{K} \gamma_{m l}\right)\right]\right\} \]

分步求解 \[ g(\alpha) = \frac{\partial L}{\partial \alpha_{k}}=M\left[\Psi\left(\sum_{l=1}^{K} \alpha_{l}\right)-\Psi\left(\alpha_{k}\right)\right]+\sum_{m=1}^{M}\left[\Psi\left(\gamma_{m k}\right)-\Psi\left(\sum_{l=1}^{K} \gamma_{m l}\right)\right] \]

\[ H(\alpha) =\frac{\partial^{2} L}{\partial \alpha_{k} \partial \alpha_{l}}=M\left[\Psi^{\prime}\left(\sum_{l=1}^{K} \alpha_{l}\right)-\delta(k, l) \Psi^{\prime}\left(\alpha_{k}\right)\right] \]

解得参数的估计值 \[ \alpha \leftarrow \alpha - H(\alpha)^{-1} g(\alpha) \]