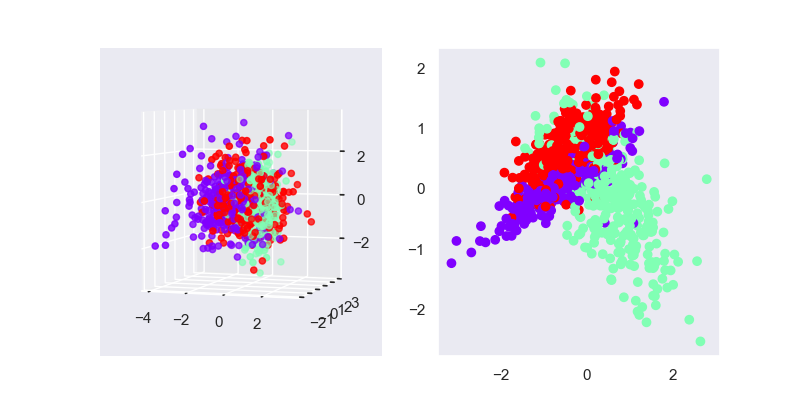
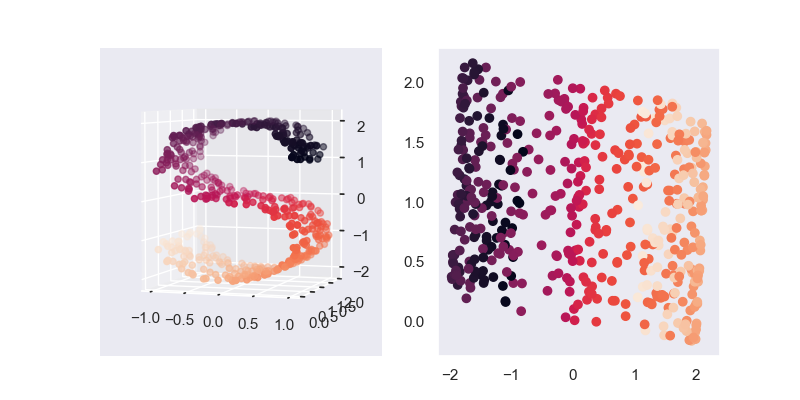
实现代码传送门
主成分分析(Principal Component Analysis,PCA)是一种以样本间的方差为基础的降维算法。
1. 输入输出
训练输入: \[ X = [x_{ij}]_{m \times n} \] 测试输入 \[ X' = [x'_{ij}]_{m \times n} \] 测试输出: \[ \hat X' = [\hat x'_{ij}]_{m \times k} \]
2. 模型效果
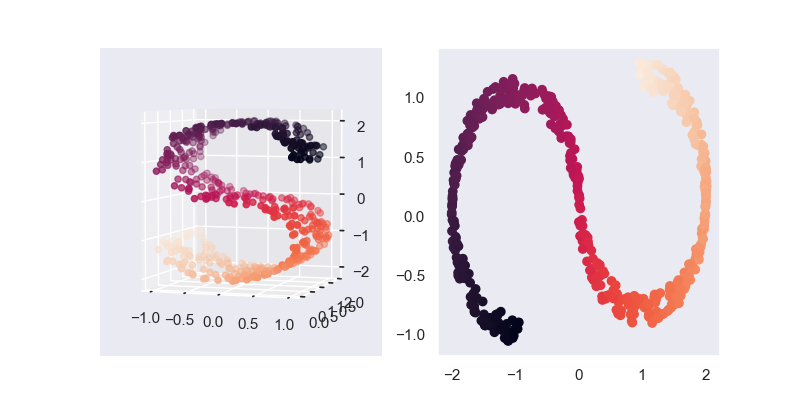
在SVD的作图中,我们采用了 \(AV_k\) ,而PCA中,其对应的是 \(U_kA\),所以一种快速的PCA算法是直接对原始的矩阵进行SVD
对于两者的区别,可以理解为前者是将 \(A\) 作为变换坐标系,需要求原坐标系的数据,即将初始数据在 \(A\) 中表现出来;后者则将\(A\) 作为原始坐标系的数据,需要求变换后的坐标系,即将 \(A\) 在变换后的坐标系中变现出来。
3. 模型推导
3.1. 基本定义
设原始空间 \(R^n\) 中的基坐标系为 \(e=\{e_1,...,e_n\}\),于是我们通过变换坐标系,使得变换后,信息都集中在 \(k\) 个坐标系中。
所有样本点到对应坐标轴的距离之和越小,该坐标轴的信息量越大,其中,信息量最大的轴称为第一主成分,次之的称为第二主成分,以此类推。
由于信息都集中在前 \(k\) 个坐标轴中,所有后面的坐标轴的信息量很小,可以直接丢弃,达到数据压缩的目的。
在推导前,先给出如下定义
- 原始数据已经经过标准化,即 \(\mu_i =E[x_i]= \frac{1}{n} \sum_i^n x_{i}=0\)
- 为了后续推导方便,我们对 \(X\) 进行转置,即 \(X \leftarrow X^T \in R^{n\times m}\)
- 投影变换后的标准正交基(即 \(w_i^Tw_i=1,w_i^Tw_j=0\))为 \(W=[w_{ij}]_{n \times n}\);
- 降维后的基坐标系为 \(W_k=[w_{ij}]_{n \times k}\),即直接丢弃了 \(n-k\) 维的空间;
- \(X\) 变换后的矩阵为 \(Y = W^TX \in R^{n \times m}\),其中,\(y^{(j)} = W^T x^{(j)}\)
于是,最终输出矩阵为 \(X'=X^TW_k\)
3.2. 学习策略
3.2.1. 最大可分性
对于变换后,任意两个向量的投影应该趋向于完全可分不重叠,即完全正交、相互独立的,即最大数据压缩率。
而两个向量的协方差越大,表示两个变量的相关性越小,于是问题可以转化为求变换后任意两点之间的协方差之和的极大值。
设降维前数据域 \(X\) 的协方差矩阵为 \(C=[c_{ij}]_{n \times n}\),其中 \[ \begin{aligned} c_{ij} &= Cov(x_{i}, x_j) \\&= E[(x_i-E[x_i])(x_j-E[x_j])] \\&= E[x_ix_j] \\&= \frac{1}{n} \sum_k^m x_{ik} x_{jk} \\&= \frac{1}{n} x_ix_j^T \end{aligned} \] 故 \[ C=\frac{1}{n} XX^T \] 由上同理可得降维后数据域 \(Y\) 的协方差矩阵为 \[ \begin{aligned} D &=\frac{1}{n} Y Y^{T} \\&=\frac{1}{n}(W^T X)(W^T X)^{T} \\&=\frac{1}{n} W^T X X^{T} W \\&=W^T C W \end{aligned} \] 要使协方差的和最大化,即求 \(\operatorname{tr}(D)\) 的极大值,即可得目标函数 \[ \begin{array}{ll} \max_{W} &\quad \operatorname{tr}\left(W^T C W \right) \\ \text{s.t.} &\quad W^TW=I \end{array} \]
3.2.2. 最小投影距离
对于变换后的数据,其还原会原始数据时,所有点变换前后的距离之和应当是最小的,即最小信息损失率。
设由 \(\bar{x}^{(i)} = W^T y^{(i)}\) 是由 \(y^{(i)}\) 还原得到的向量,所有点变换前后的距离之和为 \[ \begin{aligned} r &= \sum_{i=1}^{m}\left\|\bar{x}^{(i)}-x^{(i)}\right\|_{2}^{2} \\ &=\sum_{i=1}^{m}\left\|W^T y^{(i)}-x^{(i)}\right\|_{2}^{2} \\&=\sum_{i=1}^{m}\left(W^T y^{(i)}\right)^{T}\left(W^T y^{(i)}\right)-2 \sum_{i=1}^{m}\left(W^T y^{(i)}\right)^{T} x^{(i)}+\sum_{i=1}^{m} x^{(i) T} x^{(i)} \\&=\sum_{i=1}^{m} y^{(i) T} y^{(i)}-2 \sum_{i=1}^{m} y^{(i) T} W x^{(i)}+\sum_{i=1}^{m} x^{(i) T} x^{(i)} \\&=\sum_{i=1}^{m} y^{(i) T} y^{(i)}-2 \sum_{i=1}^{m} y^{(i) T} y^{(i)}+\sum_{i=1}^{m} x^{(i) T} x^{(i)} \\&=-\sum_{i=1}^{m} y^{(i) T} y^{(i)}+\sum_{i=1}^{m} x^{(i) T} x^{(i)} \\&=-\operatorname{tr} \left(YY^T\right)+\operatorname{tr} \left(XX^T\right) \\&=-n\cdot\operatorname{tr}\left(W^T C W \right)+\operatorname{tr} \left(XX^T\right) \end{aligned} \]
目标函数为 \[ \begin{array}{ll} \min_{W} &\quad -m\cdot\operatorname{tr}\left(W^{T} C W\right)+\operatorname{tr} \left(XX^T\right) \\ \text{s.t.} &\quad W^TW=I \end{array} \]
3.3. 学习算法
可以看出,上述两种方法最终的目标函数是一致的。下面取最大可分性的目标函数进行分析
首先,要求解 \(\operatorname{tr}\left(W^TCW\right)\) 的极大值,即使所有的 \(w^TCw\) 都尽可能大,由于 \(C\) 是一个正交角对称矩阵,所以其必然有 \(n\) 个非重根,但实际上,我们只需要求取 \(k\) 个解即可,所以问题转化为求取 \(k\) 个最大的 \(w^TCw\)
接着,看到最值约束问题,我们的老朋友拉格朗日又来了。
设对偶算子为 \(\lambda\),则 \[ J(W) = w^TCw + \lambda (1 - w^Tw) \]
令其对 \(W\) 的偏导为0,即 \[ \frac{\partial J }{\partial w } = Cw - \lambda w = 0 \] 可得 \[ Cw = \lambda w \] 可以看出,\(\lambda\) 和 \(w\) 分别为 \(C\) 的特征值和特征向量,于是所有的 \(\lambda\) 中的前 \(k\) 个最大值即为目标函数的前 \(k\) 个最优解。
3.3.1. 算法总结
最终的学习算法流程总结如下:
- 对原始样本进行标准化 \(x_i \leftarrow \frac{x_i - \mu}{\sigma}\),并对 \(X\) 进行转置 \(X \leftarrow X^T\)
- 计算 \(C=\frac{1}{n} XX^T\),如果原始数据没有进行标准化,则直接按定义计算协方差矩阵 \(C=[c_{ij}]_{n \times n}\),但数据量较大的时候不建议直接计算协方差矩阵
- 对 \(C\) 进行特征值分解
- 取 \(C\) 的前 \(k\) 个最大的特征值 \(\lambda\) 对应的向量 \(w\),并以此作为列向量,组合成矩阵 \(W_k=[w_{ij}]_{n \times k}\)
- 输出 \(X'=X^TW_k\)
4. references
《统计学习方法》16章,李航
《机器学习》10.3节,周志华
主成分分析(PCA)原理总结 - 刘建平Pinard - 博客园
See you~