1. 输入输出

Input:

样本空间 \[ X= \{x_1, x_2, ..., x_N\},x_i \in \mathbb{R}^n \] 需要划分的类簇个数 $k$

Output:

样本空间中每个点的预测类别 \[ Y=\{y_1,y_2,...,y_{N}\},y_i \in \{0,1,...,k\} \] 类簇集合 \[ C=\{C_1,C_2,...C_k\},C_i=\{x \in X | y = y_i \} \]

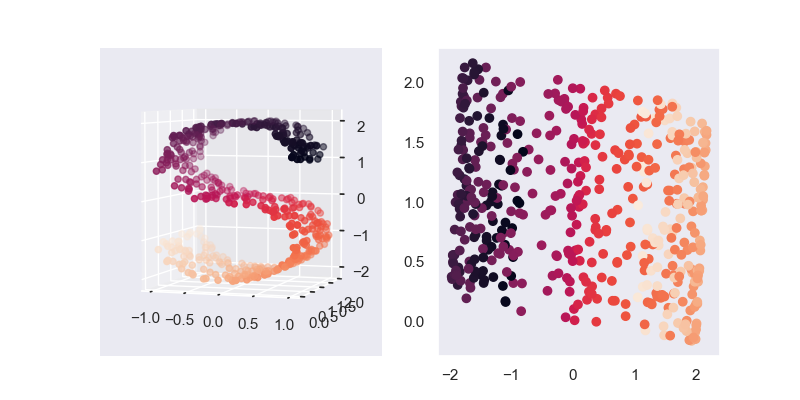
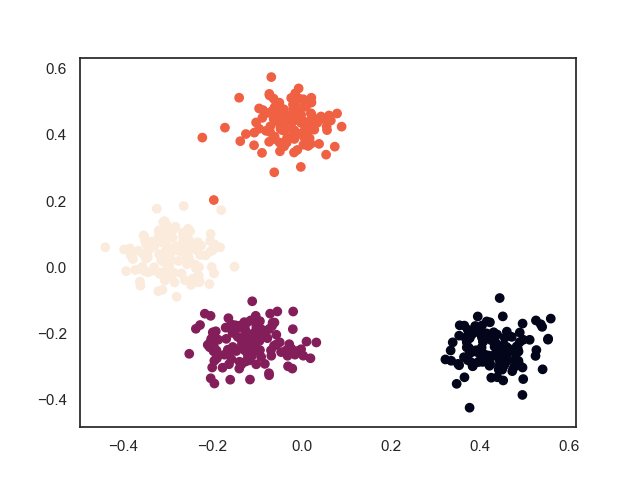
2. 模型效果

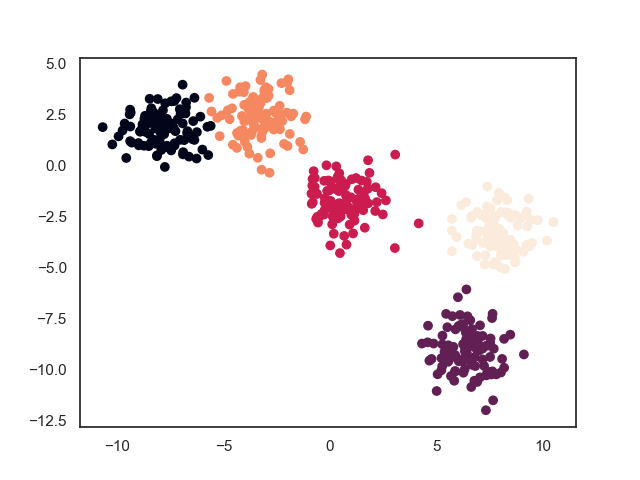
3. 模型推导

3.1. 学习策略

3.1.1. 无向权重图

谱聚类假设样本空间中的每个点都以一条无向边相连，整个样本空间便形成了一张图。

这里需要一些关于图的知识，可以翻阅之前的笔记数据结构-图，这里不多赘述。

对此，我们可以得到其邻域矩阵 $W=[w_{ij}]_{N\times N}$，及其每个样本点的度 $d_i = \sum_{j=1}^N w_{ij}$，以所有样本点的度为值，组成一个度的对角矩阵 $D = diag(d_{1},...d_N)$

至于 $W$ 矩阵值的具体计算，可以通过计算样本点的距离的相似矩阵 $S$ 来获取，一般情况下，直接认为$W=S$即可。

相似矩阵应该具有如下性质：样本点之间的距离越近，相似度越大；样本点之间的距离越远，相似度越小

原作者给出了3个可用的方法：$\epsilon$-近邻法、k近邻法、全连接法。这里只介绍用得最多的全连接法。

之所以叫全连接，是因为每个点都有对应的权值，即 $w_{ij} > 0$。可以使用多项式核函数，高斯核函数和Sigmoid核函数，其中最常用的是高斯核函数RBF，下面给出其计算公式 \[ w_{i j}=s_{i j}=\exp \left(-\frac{\left\|x_{i}-x_{j}\right\|_{2}^{2}}{2 \sigma^{2}}\right) \]

3.1.2. 无向图切图

我们一开始假设聚类前所有的点相互相连，那么聚类操作就是将部分点之间的连接切断，剩下相互连接的点组成一个簇，即所谓的切图操作。切图的最终结果是使得整个样本空间被切分成 $k$ 个簇。

首先定义两个簇 $(C_a,C_b)$ 之间的权重为 \[ W(C_a,C_b) = \sum_{i \in C_a,j \in C_b} w_{ij} \] 按照聚类指标，聚类使得簇间距离最大化，簇内距离最小化。对应到用图的文字对其进行进行转述：分割使得连接不同子图的边的权重（相似度）尽可能低，同子图内的边的权重（相似度）尽可能高。

所以可以如下计算出簇间距离（所有去掉的边的权值之和） \[ cut(C_1,...,C_k) = \frac{1}{2} \sum_{i=1} W(C_i,\overline{C_i}) \] 其中，$\overline{C_i}$ 是 $C_i$ 的补集（即 $C-C_i$）。

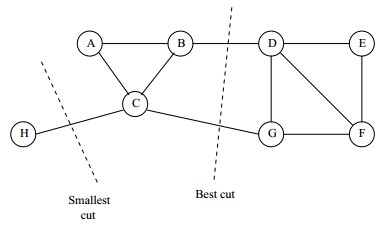
如果仅以此作为目标函数，往往会出现以下非最优聚类结果的情况：

上图中可以看出一般情况下只切断一处都会比切断两处的权值和要小，但明显这并非左右切断方案。

于是，需要对目标函数进行改进。这里，“簇内距离最小化”这个指标并没有被考虑，所以，一般采用簇内样本点数量这一约束条件对该指标进行量化。由此，产生如下两种不同的改进方案

Ratio Cut \[ RatioCut(C_1,...,C_k) = \frac{1}{2} \sum_{i=1} \frac{W(C_i,\overline{C_i})}{|C_i|} \]
Normalized Cut \[ RationCut(C_1,...,C_k) = \frac{1}{2} \sum_{i=1} \frac{W(C_i,\overline{C_i})}{vol(C_i)} \] 其中，$vol(C_j) = \sum_{i \in C_j} d_i$

其中，Ncut的效果会比较好，所以一般采用Ncut的改进方案。

3.2. 最小化目标函数

上面两种改进的目标函数的优化思想是一致的，下面只以RatioCut为例进行分析，Ncut的优化如法炮制即可。

首先，要最小化上述这个式子，我们需要用到拉普拉斯矩阵这个工具。

拉普拉斯矩阵（Laplacian matrix），也称为基尔霍夫矩阵，是表示图的一种矩阵。其定义为 \[ L = D - W \] 拉普拉斯矩阵的性质如下：

拉普拉斯矩阵是对称矩阵，这可以由 $D$ 和 $W$ 都是对称矩阵而得。

由于拉普拉斯矩阵是对称矩阵，则它的所有的特征值都是实数。

对于任意的向量 $f$ 有 \[ \begin{array}{ll}f^{T} L f &=f^{T} D f-f^{T} W f \\ &=\sum_{i=1}^{n} d_{i} f_{i}^{2}-\sum_{i, j=1}^{n} w_{i j} f_{i} f_{j} \\ &=\frac{1}{2}\left(\sum_{i=1}^{n} d_{i} f_{i}^{2}-2 \sum_{i, j=1}^{n} w_{i j} f_{i} f_{j}+\sum_{j=1}^{n} d_{j} f_{j}^{2}\right) \\ &=\frac{1}{2} \sum_{i, j=1}^{n} w_{i j}\left(f_{i}-f_{j}\right)^{2}\end{array} \]

拉普拉斯矩阵是半正定的，且对应的n个实数特征值都大于等于0，即$0=\lambda_1≤ \lambda_2≤...≤\lambda_n$，且最小的特征值为0，其对应的特征向量为 $I$ （这个由性质3可以得出）。由瑞利商可得， $f^TLf$ 的值为 $L$ 的特征值。

特征值与特征向量

对于矩阵 $A$ ，存在一个列向量 $\vec{v}$，使得 $A\vec{v} = \lambda \vec{v}$，则称 $\vec{v}$ 是 $A$ 的特征向量，$\lambda$ 为 $A$ 的特征值。

瑞利商

设 $x$ 为非零向量， $A$ 为 $n\times n$ 的Hermitan矩阵，假设 $A$ 为实矩阵

Hermitan矩阵就是满足共轭转置矩阵和自己相等的矩阵，即 $A^H=A$。如果我们的矩阵A是实矩阵，则满足 $A^T=A$ 的矩阵即为Hermitan矩阵。所以明显的，一个实的对角矩阵必然是一个Hermitan矩阵

则定义瑞利商为 \[ R(A,x) = \frac{x^TAx}{x^Tx} \] 不加证明地给出其性质：它的最大值等于矩阵 $A$ 最大特征值，而最小值等于矩阵 $A$ 的最小特征值

特别地，当 $x^Tx=1$ 时，$R(A,x)=x^TAx$

我们继续将瑞利商推广至广义瑞利商 \[ R(A,B,x)=\frac{x^TAx}{x^TBx} \] 其中，$A$ 和 $B$ 都是 $n\times n$ 的Hermitan矩阵，且 $B$ 是正定矩阵

令 $x= B^{-1/2}x'$，则 $x^TAx=x'^T(B^{-1/2})^TAB^{-1/2}x'=x'^T(B^{-1}A)x'$ ，$x^TBx=x'^T(B^{-1/2})^TBB^{-1/2}x'=x'^Tx'$，得 \[ R(A,B,x')=\frac{x'^T(B^{-1}A)x'}{x'^Tx'} \] 于是，广义瑞利商的最大值等于矩阵 $B^{-1}A$ 最大特征值，而最小值等于矩阵 $B^{-1}A$ 的最小特征值

我们引入一个指示矩阵 $H=[h_{ij}]_{N \times k}$，其定义为 \[ h_{i j}=\left\{\begin{array}{ll}0 & x_{i} \notin C_{j} \\ \frac{1}{\sqrt{\left|C_{j}\right|}} & x_{i} \in C_{j}\end{array}\right. \] 于是，对于 $(h^{(i)})^TLh^{(i)}$有 \[ \begin{aligned} (h^{(i)})^TLh^{(i)} &=\frac{1}{2} \sum_{m=1} \sum_{n=1} w_{m n}\left(h_{mi}-h_{ni}\right)^{2} \\ &=\frac{1}{2}\left(\sum_{m \in C_{i}, n \notin C_{i}} w_{m n}\left(\frac{1}{\sqrt{\left|C_{i}\right|}}-0\right)^{2}+\sum_{m \notin C_{i}, n \in C_{i}} w_{m n}\left(0-\frac{1}{\sqrt{\left|C_{i}\right|}}\right)^{2}\right)\\ &=\frac{1}{2}\left(\sum_{m \in C_{i}, n \notin C_{i}} w_{m n} \frac{1}{\left|C_{i}\right|}+\sum_{m \notin C_{i}, n \in C_{i}} w_{m n} \frac{1}{\left|C_{i}\right|}\right)\\ &=\frac{1}{2}\left(c u t\left(C_{i}, \bar{C}_{i}\right) \frac{1}{\left|C_{i}\right|}+\operatorname{cut}\left(\bar{C}_{i}, C_{i}\right) \frac{1}{\left|C_{i}\right|}\right) \\ &=\frac{\operatorname{cut}\left(C_{i}, \bar{C}_{i}\right)}{\left|C_{i}\right|} \end{aligned} \]

再进一步地，我们有 \[ \text{RationCut}(C_1,...,C_k) = \sum_{i=1}^{k} (h^{(i)})^TLh^{(i)}=\sum_{i=1}^{k}\left(H^{T} L H\right)_{i i}=\operatorname{tr}\left(H^{T} L H\right) \] 由于每一个元素都只能放在一个类里面，所以 $h$ 是一个正交向量，即 $h^Th=1$，于是，最终的优化问题为 \[ \begin{array}{ll} \min_{H} &\quad \operatorname{tr}\left(H^{T} L H\right) \\ \text{s.t.} &\quad H^TH=I \end{array} \] 但是对于 $H$，一共有 $k2^N$ 种可能的取值，上述的优化问题属于NP难问题。

首先，求解 $\operatorname{tr}\left(H^{T} L H\right)$ 的最小值，即求解所有 $(h^{(i)})^TLh^{(i)}$ 之和的最小值，问题可以简化为求 $(h^{(i)})^TLh^{(i)}$ 前k个最小值。

而根据拉普拉斯矩阵的性质4，我们可知 $(h^{(i)})^TLh^{(i)}$ 的最小值即为 $L$ 的最小特征值，此时 $L$ 的特征向量为 $h^{(i)}$ ，此时的特征向量即为系统的最优聚类结果（这里应用了降维相关的概念）。

这里就是谱聚类名字的由来。矩阵的谱为矩阵的特征值。

上面结论的简单证明如下：

设$Lh = \lambda h$，则 $h$ 是 $L$ 的特征向量，$\lambda$ 为 $L$ 的特征值，加入 $h^T$ 得 $h^TLh=\lambda h^Th=\lambda I$，即可推出上述结论

特别地，这里取最小特征值是出于最优化的习惯，将拉普拉斯矩阵定义为 $L=D-W$ ，如果将其定义为 $L=W-D$ ，则取最大特征值。

如果使用Ncut方案，则需要计算的为 $L$ 的标准化矩阵 $D^{-1/2}LD{-1/2}= $ ，就没有不用考虑需要计算最大值还是最小值的问题，只要计算最小特征值即可。

但是，该聚类结果是以0作为分类界限，将样本划分为 $C_j$ 和 $\bar{C_j}$ 两类，只是一个二聚类器。所以，需要取前 $k' > \log k$ （实际应用中，一般取 $k'=k$ ）个最小特征值，便得到 $k'$ 个特征向量，组成特征矩阵 $H' = [h'_{ij}]_{N \times k'}$，该矩阵矩阵中包含了 $k'$ 个划分中心，所以最后对其进行一次传统的聚类（如Kmeans聚类等）即可得到一个 $k$ 类聚类器。

这里Kmeans其物理概念已经不再是之前的提到的那样了，更多是跟集成学习的概念类似。

于是，最终将离散的聚类问题松弛为连续的特征向量进行求解，因此，我们最终不需要直接求解是怎样切图，只需要间接地求取特征向量即可，真是相当巧妙。

3.3. 学习算法

最后总结一遍总的学习过程

计算权值矩阵 $W=[w_{ij}]_{N\times N}$，其中，$w_{i j}=\exp \left(-\frac{\left\|x_{i}-x_{j}\right\|_{2}^{2}}{2 \sigma^{2}}\right)$
计算度对角矩阵 $D = diag(d_{1},...d_N)$，其中，$d_i = \sum_{j=1}^N w_{ij}$
计算拉普拉斯矩阵 $L=D-W$
计算 $L$ （如果使用Ncut改进方案，这里输入的是 $L$ 的标准化矩阵 $D^{-1/2}LD{-1/2}= $ ）的前 $k$ 个最小特征值对应的特征向量组成的特征矩阵 $H' = [h'_{ij}]_{N \times k'}$，其中的每一行可以表示原样本空间中对应向量
对 $H'$ 进行Kmeans聚类，其聚类结果即为原样本空间的聚类结果