1. 集成学习
集成学习(ensemble learning)是一种分类算法,准确来说是一个关于分类模型集合的系统,其基本思想是,将多个弱学习器联合,变成一个强学习器。
每个弱分类的种类应保持一致,此时,单个弱分类器也被称为基分类器,基分类器可以是任意分类算法。但由于决策树、神经网络等模型对输入数据敏感,容易生成多样性丰富的个体分类器,所以非常适合做基分类器(事实上,你会发现书中,包括千篇一律的博客中,使用得到例子的基分类器都是决策树),而其他像朴素贝叶斯、线性/对数模型、KNN、SVM等对输入数据不敏感的稳定基分类器,理论上通过认为创造一些噪声,也可以作为基分类器。
每个弱分类器越是好而不同,最终系统的预测效果越好。
集成学习一般分为串行的boosting学习和并行的bagging(Bootstrap AGGregatING,自助抽样集成)学习。
2. Adaboost
Adaboost(Adaptive boosting,自适应增强)算法是boosting学习的典型。
实现代码传送门
2.1. 输入输出
训练输入: \[ T=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中,
- \(x\) 为特征域,\(x_i \in \mathbb{R}^{n},i =1,2,...,N\)
- \(y\) 为标签域,\(y_i \in \{-1,+1\}\) ,\(K\) 为输出标签集合大小。
测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^n \] 测试输出: \[ Y'=\{y'_1,\cdots,y'_{N'}\},y_i' \in \{-1,+1\} \]
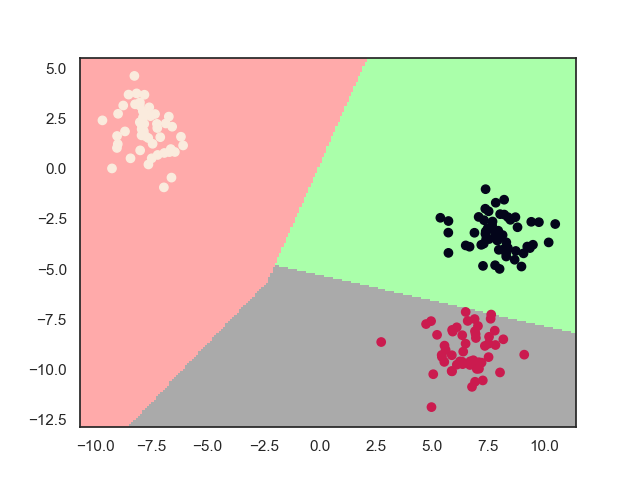
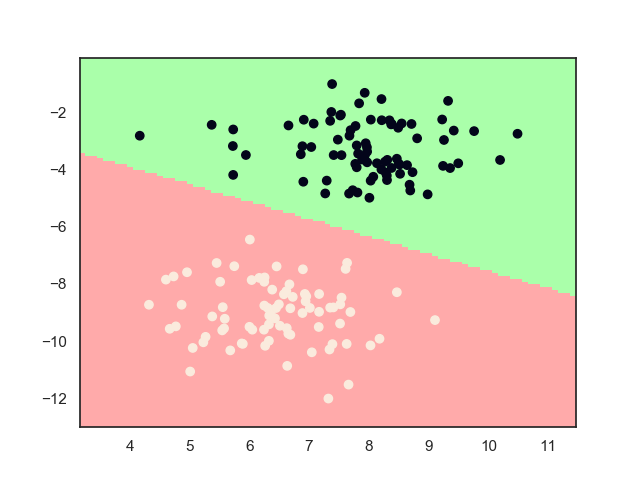
2.2. 模型效果
2.3. 模型推导
2.3.1. 基本方法
由于直接求解整个模型集合的损失函数是一件很困难的事情,所以加性模型的思想是,将模型集合中变成时序集合,即前一个模型的输出作为后一个模型输出的一部分,每次从后往前求解集合中每个模型的损失函数,最后再递归地从前往后更新参数。这种算法也被称为前向分布算法
Adaboost算法的思想为,只有第一个基分类器是通过初始数据得到的,后面的分类器都是基于前一个分类器迭代生成的。迭代生成的思想是,提高前一个前一个弱分类器错误样本的权值,而降低分类正确的权值,即对后一个分类器来说,其偏向于关注前一个分类器错误分类的样本(即提取更多错误分类的样本),将其矫正,即序列抽样的思想;至于每一个分类器,也有输出的权值,表示该分类器在表决中的重要程度。
这其实是很好理解的,例如,这里a和b进行讨论,a首先提出自己的观点,b认为a的某些观点错误,提出了自己的错误矫正建议,但裁判认为a的声望比b的高,所以采用a的大部分观点和b的小部分观点
这其实就是一种残差逼近的思想,其实也可以将其看做是一个改进的决策树(从模型效果图中也可以看出这一点),每个模型就是一个分类节点,通过分类节点不断地逼近正确分类。这种逼近效率很高,其训练误差是指数级下降的。
为了保证分类器的多样性,每次分类时,从 \(n\) 个特征中随机抽取一个特征(也有选择误差率最小的特征)进行优化,所以下面推导中的 \(x\) 也是一维的。
废话说完了,下面开始正式推导。
设基分类器模型函数为 \(G_m(x)\),其输出权值为 \(\alpha_m\)
则第\(m\)个模型输出为 \[ f_m(x) = f_{m-1}(x) + \alpha_m G_m(x) \] 最终模型输出为 \[ f(x) = f_M(x) = \sum_{m=1}^M \alpha_m G_m(x) \] 又由于输出一个分类的结果,则系统的模型函数为 \[ f(x)= sign(\sum_{m=1}^M \alpha_m G_m(x)) \]
Adaboost还有一种特殊情况,基函数为决策树,并且每个模型没有输出权值,我们把这种模型称为提升树(boosting tree)
设基分类器模型函数为 \(T_m(x)\),系统函数为 \[ f(x) = \sum_{m=1}^M T_m(x) \]
2.3.2. 学习算法
设模型的损失函数为 \(L(y,f(T))\),优化问题为极小化该损失函数,即 \[ \min_{\alpha, G} \sum_{i=1}^N L(y_i,\sum_{m=1}^M \alpha_m G_m(x_i)) \]
根据前向分布算法,每一步只学习一个基函数及其系数,逐步逼近优化目标函数。即
\[ \min_{\alpha, G} \sum_{i=1}^N L(y_i,\alpha G(x_i)) \] 又设损失函数为指数损失函数 \[ L(y,f(x)) = \exp(-yf(x)) \]
于是,每一次的优化问题的求解为 \[ (\alpha_m, G_m) = \arg \min_{\alpha, G} \sum_{i=1}^N L(y_i,f_{m-1} (x_i)+ \alpha G_{m}(x_i)) \\ = \arg \min_{\alpha, G} \sum_{i=1}^N \overline w_{mi} \exp(-y_i\alpha G(x_i)) \]
其中,\(\overline w_{mi} = \exp(-y_i f_{m-1}(x_i))\),因为 \(\overline w_{mi}\) 并不依赖于 \(\alpha\) 或 \(W\) ,所以与最小化无关,但依赖 \(f_{m-1}(x_i)\) ,所以会随着迭代更新
由于 \(y_i \in \{ -1, 1\}\),解得 \[ G_m = \arg \min_{G} \sum_{i=1} ^N \overline w_{mi} I(y_i \neq G(x_i)) \] 又 \[ \alpha_m = \sum_{y_i=G_m(T_i)} \overline w_{mi} e^{-\alpha} + \sum_{y_i \neq G_m(T_i)} \overline w_{mi} e^{\alpha} \\ = (e^{\alpha} - e^{-\alpha}) \sum_{i=1}^N \overline w_{mi} I(y_i \neq G(x_i)) + e^{-\alpha} \sum_{i=1} ^N \overline w_{mi} \] 代入已求得的 \(G_m\) 后,对其求导,并使其导数为0,解得 \[ \alpha_m = \frac{1}{2} \ln \frac{1-e_m}{e_m} \] 其中,\(e_m\) 为分类误差率 \[ e_m = \frac{\sum_{i=1}^N \overline w_{mi} I(y_i \neq G(x_i))}{\sum_{i=1}^N \overline w_{mi} } \\ = \sum_{i=1}^N w_{mi} I(y_i \neq G(x_i)) \]
其中, \(w_{mi}\) 为当前模型的权值,为了使每个模型的权值分布一致,加入规范化因子\(Z_m\) ,则第 \(m+1\) 个分类器的权值更新为
\[ w_{m+1,i} = \frac{w_{mi}}{Z_m} \exp(-\alpha_my_if_m(x_i)) \] 其中,\(Z_m\) 为 \[ Z_m = \sum_{i=1}^N w_{mi} \exp(-\alpha_my_if_m(x_i)) \] # 随机森林
随机森林(Random Forest,RF)算法是Bagging学习的典型。
实现代码传送门
2.4. 输入输出
训练输入: \[ T=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中,
- \(x\) 为特征域,\(x_i \in \mathbb{R}^{n},i =1,2,...,N\)
- \(y\) 为标签域,\(y_i \in \{c_1,\cdots,c_K\}\) ,\(K\) 为输出标签集合大小。
测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^n \] 测试输出: \[ Y'=\{y'_1,\cdots,y'_{N'}\},y_i' \in \{c_1,\cdots ,c_K\} \]
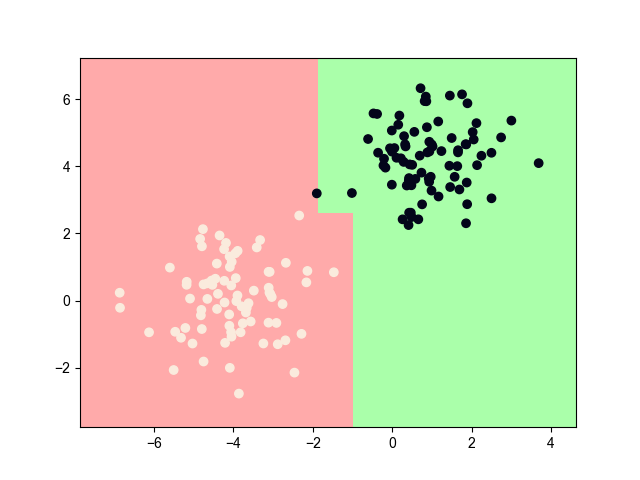
2.5. 模型效果

2.6. 模型推导
2.6.1. 基本方法
Bagging学习的思想为,同时训练多个分类器,然后对这些分类器的预测结果通过投票法得出最终的分类结果。
为了保证每个分类器的多样性,Bagging学习其采用自助采样法为每个基分类器准备训练样本,即每次有放回地抽取一个样本,直到抽取出 \(N\) 个样本。这样,作为基分类器的输入样本中,有的样本会重复出现,有的样本根本不会出现。
RF对bagging进行扩展,不仅随机抽取输入样本,在决策树的每个节点进行分裂是,由原先在所有维度中选择增益最大的维度,变为随机在 \(m'\ll m\) 个维度中寻找,这已经不仅仅只有数据扰动了,还有属性扰动,大大加强的抗过拟合能力。
设基分类器模型函数为 \(G_m(x)\),则系统函数为 \[ f(x) = \arg \max_{y \in Y} \sum_{m=1}^M I(G_m(x) = y) \]
3. 多样性增强
为了增强基分类器的多样性,一般采用以下方法加入噪声
数据样本扰动
这是针对不稳定基分类器增强多样性的常用方法,通常通过随机采样完成,例如Adaboost中的序列采样,记忆bagging的自助采样。
输入属性扰动
从输入特征中随机选取 \(m'\ll m\) 个特征进行优化,例如Adaboost随机特征抽取,以及RF中的随机特征分裂
输出表示扰动
对某些类的标签进行互换,例如a分类学习的标签是1和-1,则b分类器学习的标签为-1和1
算法参数扰动
每个分类器的参数随机生成
4. references
《统计学习方法》第8章,李航
《机器学习》第8章,周志华
To be continue~