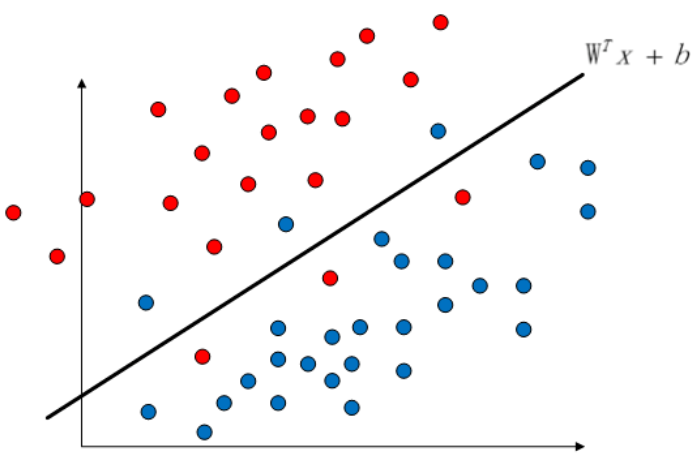
支持向量机(Support Vector Machines,SVM)是一种基于感知机的分类算法。
一般第一次接触支持向量机都会把支持当做动词,但这里应该将其当做形容词,意为一种把支持划分平面的向量当做分类标准的机器
基于numpy的实现代码传送门
1. 输入输出
训练输入: \[ T=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中,
- \(x\) 为特征域,\(x_i \in \mathbb{R}^{n},i =1,2,...,N\)
- \(y\) 为标签域,\(y_i \in \{-1,+1\}\)
测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^n \] 测试输出: \[ Y'=\{y'_1,\cdots,y'_{N'}\},y_i' \in \{-1,+1\} \]
2. 模型效果
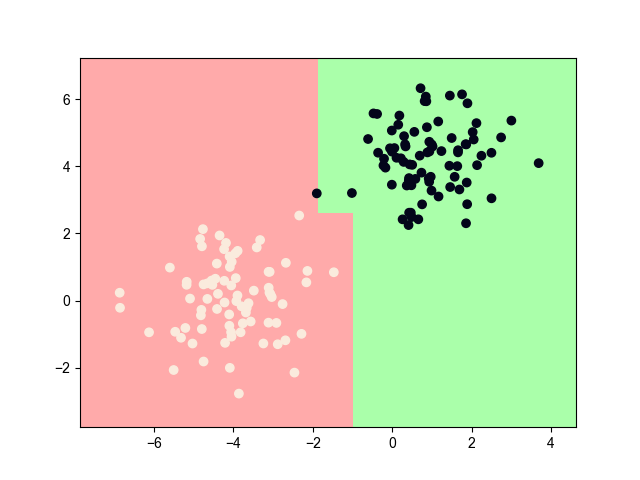
2.1. 训练效果
其中,蓝线为间隔边界,在蓝线上的点为支持向量
2.2. 最终结果
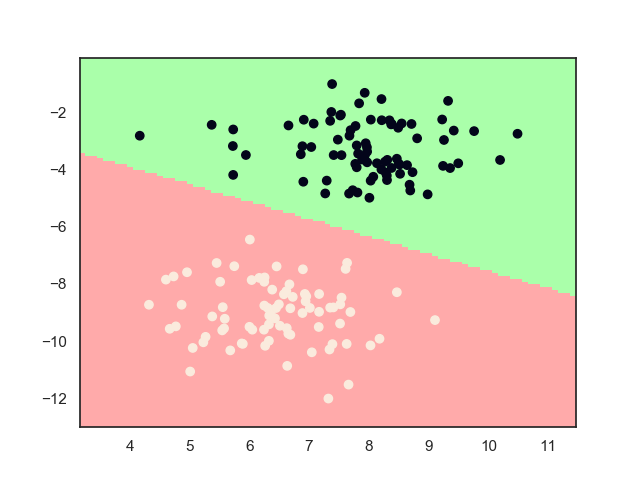
3. 模型推导
3.1. 基本方法
再次回到感知机。
感知机利用误分类最小策略,求得分离超平面,但存在无穷多的解。于是,SVM在这个基础上,继续往前推导,在感知机的解集中,寻找一个间隔最大化的唯一解,该解就是最优分离超平面。
我们依然假设输入数据是线性可分。
由于SVM是感知机中的一个特殊情况,所以SVM的模型函数和感知机的模型函数是一样的 \[ f(x)=sign(w \cdot x + b ) \]
3.2. 学习策略
3.2.1. 原始问题
首先,我们定义如下两种间隔
点 \((x_i,y_i)\) 到超平面 \((w,b)\) 的函数间隔为 \[ \hat \gamma = y_i (w \cdot x_i+b) \] 其代表了分类的正确性和确信度
在这基础上再加上规范化,就得到了几何间隔 \[ \gamma = \frac{\hat \gamma}{||w||} \] 设所有的训练样本到超平面的几何间隔至少为 \(\gamma\) ,这样就得到了一个集合,而SVM模型的 \(\gamma\) 应该是集合中的最大值。将其使用函数间隔表示,于是,我们得到如下优化问题 \[ \begin{array}{ll} \max_{w,b} &\quad \frac{\hat \gamma}{||w||} \\ \text{s.t.} &\quad y_i(w \cdot x_i+b) \geq \hat \gamma \\ \end{array} \] 由于函数间隔的取值不影响最优化问题的解,所以直接取 \(\hat \gamma = 1\) ,处于习惯,将最大化问题改写为最小化问题,最终得到如下优化问题 \[ \begin{array}{ll} \min_{w,b} &\quad \frac{||w||^2}{2} \\ \text{s.t.} &\quad y_i(w \cdot x_i+b) - 1 \geq 0 \end{array} \] 这是一个凸二次规划问题
3.2.2. 对偶问题
又到了熟悉的环节。
当遇到最值约束问题,第一时间想到的就是将其转换为拉格朗日对偶问题。
引入对偶算子 \(\alpha = (\alpha_1,...,\alpha_N)^T\),定义拉格朗日函数 \[ L(w,b,\alpha) = \frac{||w||^2}{2} - \sum_{i=1}^N \alpha_i y_i(w \cdot x_i+b) + \sum_{i=1}^N \alpha_i \] 原始问题的对偶问题为 \[ \max_\alpha \min_{w,b} L(w,b,\alpha) \]
3.2.3. 极小化解
分别对 \(w,b\) 求偏导,并令其等于0 \[ \nabla_w L(w,b, \alpha) = w- \sum_{i=1}^N \alpha_iy_i x_i=0 \\ \nabla_b L(w,b,\alpha) = - \sum_{i=1}^N \alpha_iy_i=0 \] 解得 \[ w = \sum_{i=1}^N \alpha_iy_i x_i \\ \sum_{i=1}^N \alpha_iy_i=0 \] 将其代入原式中,得 \[ \min_{w,b} L(w,b,\alpha) = - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) + \sum_{i=1} ^ N \alpha_i \] 于是,我们再次得到了一个对偶最值约束优化问题 \[ \begin{array}{ll} \min_{\alpha} &\quad \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum_{i=1} ^ N \alpha_i \\ \text{s.t.} &\quad \sum_{i=1}^N \alpha_iy_i=0 \\ & \quad \alpha \geq 0 \end{array} \] 由于原始问题满足相关定理(具体可以查阅李航书中附录3的相关内容),故存在 \(w,\alpha,\beta\),使得 \(w\) 是原始问题 \(L(w,b,\alpha)\) 的解,\(\alpha,\beta\) 是对偶问题 \(L'(x,\alpha,\beta)\) 的解。于是求解原始问题正式转换为求解对偶问题。
3.2.4. KKT条件
现在还有一个问题,对偶问题中并没有出现 \(w\) 变量,怎样将两者串联起来?于是,引出了KKT条件。
上面问题转换成立的充分必要条件为 \(w,\alpha,\beta\) 满足KKT条件 \[ \nabla L(w,b,\alpha) = 0 \\ \alpha_ic_i(x) = 0 \\ c_i(x) \leq 0 \\ \alpha _i \geq 0 \\ h_j(x) = 0 \] 这里,\(c_i(x) = -y_i(w \cdot x_i+b) + 1,h_j(x) \equiv 0\),特别地,条件2是一个互补条件,可以拆分成:存在 $> 0 $ ,使得 \(c_i(x) = 0\)
上述条件代入实际计算,解得 \[ w = \sum_i \alpha_iy_ix_i \\ b = y_j - \sum_{i=1}^N \alpha_i y_i (x_i \cdot x_j) \] 最终模型函数的函数也转换为 \[ f(x) = sign(\sum_{i=1}^N \alpha_i y_i (x \cdot x_i) + b) \] 于是,最终问题转化为对 \(\alpha\) 的求解,上式也被称为SVM的对偶形式
3.2.5. 软间隔
这里,我们先不着急继续对 \(\alpha\) 进行求解,因为还有一些问题需要解决,需要对约束条件打个补丁。
在一开始的时候,我们假设数据是线性可分的,那么现在我们推广至线性不可分的情况。
有趣的是,我们将支持线性可分和线性不可分的SVM都统称为线性SVM
对于线性不可分的情况,上述约束条件可能并不都满足,例如下图中存在特异点的情况
于是,我们需要将原本的硬间隔最大化,修改为软间隔最大化
对于上面情况,我们只需要忽略小部分的特异点,即可认为剩下的样本是线性可分的。为此,加入损失函数对特异点进行惩罚,一般可以取以下几种损失函数
hinge损失 \[ l(z) = \max(0,1-z) \]
指数损失 \[ l(z) = \exp(-z) \]
logistics损失 \[ l(z) = \log(1+\exp(-z)) \]
0/1损失 \[ l(z) = \left \{ \begin{array}{ll} 1, & z< 0 \\ 0, & z \geq 0 \end{array} \right . \]
如果选择logistics损失,得到的模型就几乎成为logistics回归模型了,0/1损失数学性质不太好,不容易直接求解,所以一般选择hinge损失
对于上述的hinge损失,\(z_i=y_i(w \cdot x_i+b),1-z_i \geq 0\)
引入松弛变量 \(\xi_i \geq 0\) 作为hinge损失的值,即 \(\xi_i = 1 - y_i(w \cdot x_i+b)\)
加入 \(L_2\) 正则项后,目标函数变为 \[ L = \sum_{i=1}^N \xi_i + \lambda||w||^2 \] 令 \(\lambda = \frac{1}{2C}\),优化问题变为(为了保持和原问题的格式一致,下式省略了常数项 \(\frac{1}{C}\),因为最终是 \(\arg\) 运算,所以这中省略是不影响最终结果的) \[ \begin{array}{ll} \min_{w,b} &\quad \frac{||w||^2}{2} + C \sum_{i=1} ^N \xi_i \\ \text{s.t.} &\quad y_i(w \cdot x_i+b) \geq 1 - \xi_i \end{array} \] 其中,\(C>0\) 为惩罚参数,\(C\)值越大,对误分类的惩罚越大(即越强迫所有点都满足约束条件)
最小化目标函数的意义为间隔尽可能大的同时,误分点个数尽可能少
对偶问题变为 \[ \begin{array}{ll} \min_{\alpha} &\quad \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum_{i=1} ^ N \alpha_i \\ \text{s.t.} &\quad \sum_{i=1}^N \alpha_iy_i=0 \\ & \quad 0 \leq \alpha_i \leq C \end{array} \] 最终优化问题基本不变,只是约束条件增加了一个上界
这里需要注意的是,对应的KKT条件也增加以一些条件,但后面计算中,貌似将增加的部分忽略了,没有找到这样做的理由,估计是为了计算方便?
3.3. 学习算法
3.3.1. 基本思路
终于到了最后 \(\alpha\) 学习问题。因为最终问题是凸二次规划问题,是有一个全局最优解的,但当训练样本增大时,求解全局最优往往变得很低效,所以一般采用启发式学习算法,例如序列最小最优化算法(SMO),其基本思路为:如果所有变量都满足KKT条件,则训练完成;否则,每次只改变两个变量,对其进行二次规划求解,使得目标函数值变小。
假设在一次更新中, \(\alpha_1,\alpha_2\) 为需要修改的变量,其他变量固定不变,则优化问题为 \[ \begin{array}{ll} \min_{\alpha} \quad W(\alpha_1 \alpha_2) =& \frac{1}{2}(K_{11}\alpha_1^2 + K_{22}\alpha_2^2) + y_1y_2K_{12}\alpha_1\alpha_2 \\ &+ y_1\alpha_1\sum_{i=3}^n \alpha_i y_i K_{i1} + y_2\alpha_2\sum_{i=3}^n \alpha_i y_i K_{i2} \\ &- (\alpha_1+ \alpha_2) \end{array} \]
\[ \begin{array}{ll} \text{s.t.} &\quad y_1\alpha_1 + y_2\alpha_2 = -\sum_{i=3}^N \alpha_iy_i \\ & \quad 0 \leq \alpha_i \leq C \end{array} \]
其中,\(K_{ij} = x_j \cdot x_j\)
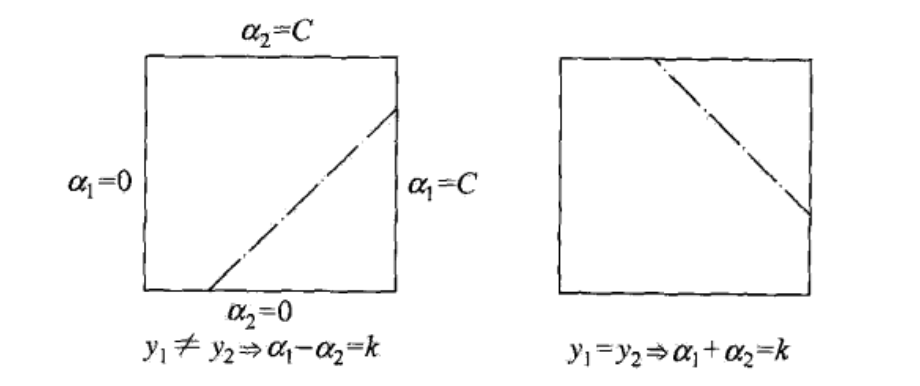
3.3.2. 确定取值边界
\(\alpha_1,\alpha_2\) 的取值范围组成了一个 \([0,C]\times[0,C]\) 的正方形区域,而更新后的值必定落在这个区间内,如下图所示
先确定 \(\alpha_2\) 的值, \(\alpha_1\) 的值也会随之确定
假设初始解为 \(\alpha_1^{old},\alpha_2^{old}\),最优解为 \(\alpha_1^{new}, \alpha_2^{new}\),则 \(\alpha_2^{new}\) 的取值范围必须满足下列条件 \[ L \leq \alpha_2^{new} \leq H \] 当 \(y_1 \neq y_2\) 时 \[ L = \max(0, \alpha_2^{old} - \alpha_1^{old}) \\ H = \min (C, C + \alpha_2^{old} - \alpha_1^{old}) \] 当 \(y_1 = y_2\) 时 \[ L = \max(0,\alpha_2^{old}+\alpha_1^{old}-C) \\ H = \min (C, \alpha_2^{old}+\alpha_1^{old}) \]
3.3.3. 未约束最优解
设 \(x_i\) 的预测值 \[ g(x_i) = \sum_{i=j}^N \alpha_j y_j K_{ij}+ b \] 则,\(x_i\) 的预测值与真实值的误差 \[ E_i = g(x_i) - y_i, i = 1,2 \] 设为考虑不约束条件时 \(\alpha_2\) 的最优解为 \(\alpha_2^{new,unc}\) ,
下面不加证明地给出如下定理(证明可查阅李航统计一书中第7章内容) \[ \alpha_2^{new,unc} = \alpha_2^{old} + \frac{y_2(E_1-E_2)}{\eta} \] 其中,\(\eta = K_{11} + K_{22} - 2K_{12}\)
则 \(\alpha_2^{new}\) 的解为 \[ \alpha_2^{new} = \left \{ \begin{array}{ll} H &, \alpha_2^{new,unc} > H \\ \alpha_2^{new,unc} &, L \leq \alpha_2^{new,unc} \leq H \\ L &, \alpha_2^{new,unc} < L \end{array} \right . \]
最后求得 \(\alpha_1^{new}\) \[ \alpha_1^{new} = \alpha_1^{pld} + y_2y_2(\alpha_2^{old}-\alpha_2^{new}) \]
3.3.4. 变量选择
还有最后一个问题——怎样选择每次改变的这两个变量
首先,第一个变量选择严重违反KKT条件的点,即不满足以下KKT条件的点 \[ \begin{array}{ll} \alpha_i = 0 \Leftrightarrow y_ig(x_i) \geq 1 &,(\text{正确分类})\\ 0 < \alpha_i < C \Leftrightarrow y_ig(x_i) = 1 &,(\text{在边界上的支持向量})\\ \alpha_i = C \Leftrightarrow y_ig(x_i) \leq 1 &,(\text{在边界之间}) \end{array} \] 其中,优先选择不满足第二个条件的样本点
然后,在第一个变量已经选择的基础上,第二个变量选择变化足够大的点
因为 \(\alpha_2^{new}\) 依赖于 \(|E_1-E_2|\) ,因为 \(E_1\)已经确定,为了加快计算速度,一种简单的做法是,如果 \(E_1\) 为正,则选择最小的 \(E_i\) 作为 \(E_2\),否则,选择最大的 \(E_i\) 作为 \(E_2\)
实际上,\(E_2\) 是随机选取都是没有问题的
特别地,一种更为快捷的选取方式为保存上一步不满足KKT条件的点,下次遍历时直接从中遍历即可,因为上一次不满足KKT条件的点,下一次大概率也不会满足,如果没有找到第二个点,则随机挑选一个即可
3.3.5. 更新 \(b\)
每次更新完两个变量后,还要重新计算阈值 \(b\)
当 \(0 < \alpha_1^{new} < C\) 时 \[ b_1^{new} = -E_1-y_1K_{11}(\alpha_1^{new} - \alpha_1^{old} - y_2 K_{21}(\alpha_2^{new} - \alpha_2^{old})) + b^{old} \] 当 \(0 < \alpha_2^{new} < C\) 时 \[ b_2^{new} = -E_2-y_1K_{12}(\alpha_1^{new} - \alpha_1^{old} - y_2 K_{22}(\alpha_2^{new} - \alpha_2^{old})) + b^{old} \] 如果,\(\alpha_1^{new},\alpha_2^{new}\) 同时满足上诉条件,则 \(b_1^{new} = b_2^{new}\);如果 \(\alpha_1^{new},\alpha_2^{new}\) 是 \(0\) 或 \(C\) ,那么,\(b_1^{new}, b_2^{new}\) 间的取值都符合KKT条件,则取两者的中值
4. 非线性SVM
现在,我们将线性扩展至非线性情况,为此,引入核技巧
对于非线性问题,一般将其变换为线性问题进行求解,最常用的方法的改变坐标系空间
设原空间为 \(X \in \mathbf{R}^n\),新空间 \(Z \in \mathbf{R}^n\),两者关系为 \(z = \phi(x)\)
对于所有的 \(x \in X\) ,有 \[ K_{ij} = K(x_i,x_j) = \phi(x_i) \cdot \phi(x_j) \] 则称 \(K(x_i,x_j)\) 为核函数,新空间称为希尔伯特空间
可以证明,适合作为核函数一定是正定核,但由于直接证明原函数矩阵是正定的比较困难,所以,一般判断其Gram矩阵 \(G=[K(x_i,x_j)]_{m \times m}\) 是半正定的
对于方阵 \(A_{n \times n}\),如果对于所有的长度为 \(n\) 的非零向量 \(x\) ,使得 \(x^TAx > 0\) 恒成立,则称 \(A\) 为正定矩阵;如果使得 \(x^TAx \geq 0\) 恒成立,则称 \(A\) 为半正定矩阵
于是对于原问题所有 \(x_i \cdot x_j\) 的内积,都可以使用其核函数代替,原模型函数表示为 \[ f(x) = sign(\sum_{i=1}^N \alpha_i y_i K(x, x_i) + b) \] 如果核函数中不包含所要求的未知变量,则这样的变换不会对最终问题的形式产生改变
对于高维计算,直接求取\(\phi(x_i) \cdot \phi(x_j)\) 非常困难,所以一般直接使用下列已经计算好的常用核函数
线性核 \[ k_{ij} = x_i \cdot x_j \]
多项式核 \[ k_{ij} = (x_i \cdot x_j + 1) ^p \] 对应的SVM为一个p次多项式分类器
高斯核 \[ k_{ij} = \exp(- \frac{||x_i-x_j||^2}{2\sigma^2}) \] 对应的SVM为一个高斯径向函数(rbf)分类器
拉普拉斯核 \[ k_{ij} = \exp(- \frac{||x_i-x_j||^2}{2\sigma}) \]
sigmoid核 \[ K_{ij} = \tanh (\beta x_i \cdot x_j + \theta) \]
5. references
《统计学习方法》第7章,李航
《机器学习》第6章,周志华
https://blog.csdn.net/v_july_v/article/details/7624837
Good night~