很多二分类器具有许多优良分类性质,但由于自身性质原因,这些二分类器无法扩展至多分类器,例如SVM等,通常会在二分类器外加上一层框架,将其应用于多分类的情况。下面以SVM为例子介绍几种通用的方法。
至于实际应用中是使用一个多分类器还是k个二分类器,得看类别情况。如果每个类别是互斥的,则使用一个多分类器,反之,则使用k个二分类器。但为了易于实现,实际上还是以使用一个多分类器为主。
实现代码传送门
0.1. 输入输出
训练输入: \[ T=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中,
- \(x\) 为特征域,\(x_i \in \mathbb{R}^{n},i =1,2,...,N\)
- \(y\) 为标签域,\(y_i \in \{c_1,\cdots,c_K\}\) ,\(K\) 为输出标签集合大小。
测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^n \] 测试输出: \[ Y'=\{y'_1,\cdots,y'_{N'}\},y_i' \in \{c_1,\cdots ,c_K\} \]
1. OvO
1.1. 基本方法
OvO(one vs. one)一对一比较
PS:怎么感觉这个算法名莫名的萌呢?:-)
顾名思义,就是每次从 \(K\) 个类别中抽取2个进行训练,从而产生 \(K(K-1)/2\) 个分类器,每个分类器都产生一个分类结果,最终结果通过投票产生。
但该算法需要计算的分类器非常多,可以加入有向有向无环图(DAG)进行优化(注意,这只是对预测进行优化,并没有缩短训练的时间)
下面是一个加了DAG优化的OvO算法
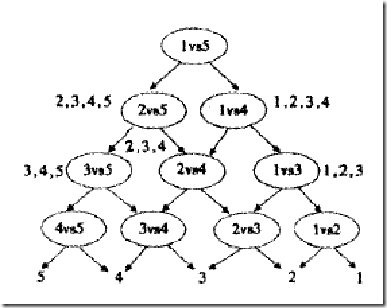
其预测流程为:首先预测“1对5”的分类结果,如果预测结果为1,则往右子树走,反之,则往左子树走;以此类推,一直走到叶子节点,就得到了分类结果。这样,只需进行 \(K-1\) 次比较即可得到结果。
但这种优化极度依赖父节点分类器的性能。例如,如果根节点分类错误,则往后所有的预测都都是错误的。一种改进的方案是,分类器还要输出分类的置信度,如果置信度不高,则两个子节点还是要再走一遍。
1.2. 模型效果
1.2.1. 训练效果
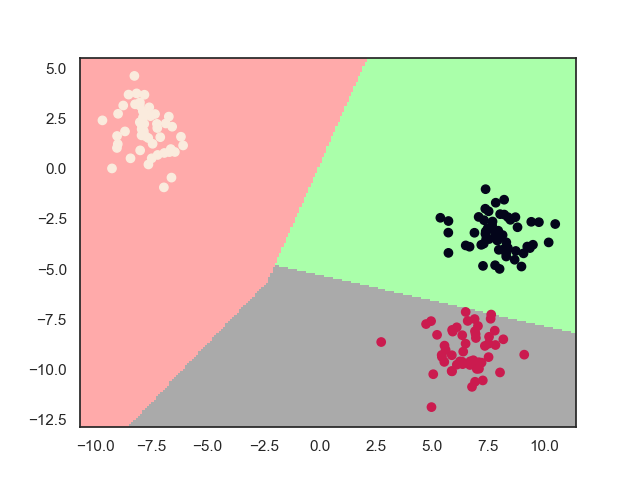
1.2.2. 最终结果
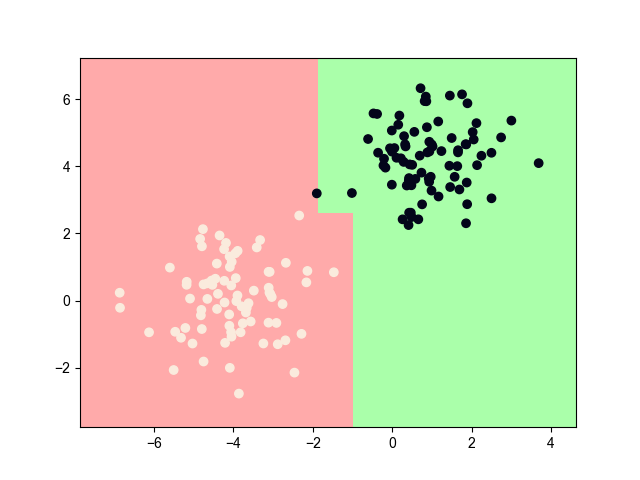
2. OvR
2.1. 基本方法
OvR(one vs. rest)一对多比较
每次从 \(K\) 个类别中选择一个作为正样本,其他作为负样本,从而产生 \(K-1\) 个分类器,同样的,最终结果也是有投票产生,但这个投票结果只从预测为正样本的分类器中产生,即“1”的那一类
这种方法的优点是减少了分类器的数量,大大降低了模型的时间成本,但缺点也很明显:会产生数据集偏斜问题。
当某些类的样本相近时,就会分类重叠的情况,即为“多”的那一类可能存在于“1”的那一类近似的样本点,这时,分类器误分了,结果该分类结果其实是被其他多个类别共享了;样本不均衡,一般上来说,正样本都是样本数较少的一类,所以分类器的预测结果都偏向于负样本。所有的情况都会造成数据集偏斜问题,即所有的分类器的预测结果极可能都为负,没人“认领”该样本点了。一种解决方法是调节惩罚因子,使得分类器更加重视正样本。另一种方法是分类器输出分类置信度,将置信度和预测结果综合考虑。
2.2. 模型效果
2.2.1. 训练效果
2.2.2. 最终结果
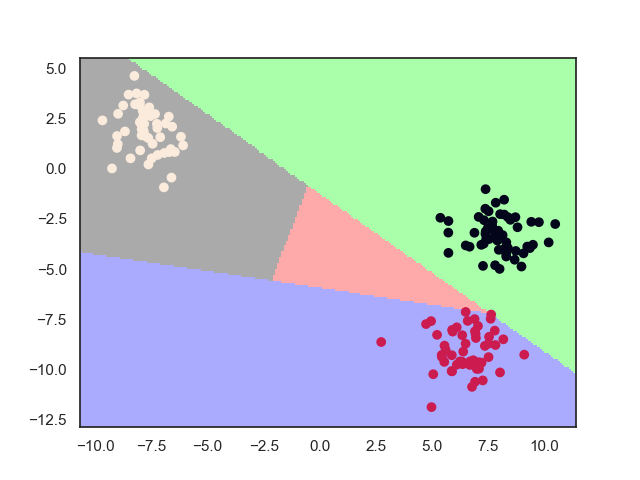
中间粉色区域为“无人认领”点的区域
3. MvM
3.1. 基本方法
MvM(many vs. many)多对多比较
每次从 \(K\) 个类别中选择若干个作为正类,若干个其他作为负类,显然,OvO和OvR是MvM的特例。
正负样本的选择一般通过纠错输出码(ECOC)进行编码
预测时,计算其汉明距离或者欧氏距离,选择距离最小的编码所对应的类作为预测结果。
这种算法的优点在于对错误有一定容忍和修正能力,ECOC编码长度越长,纠错能力越强。
ECOC编码最初就是用于解决通信传输中发生数据错误的问题,编码后增大了数据长度,但保证数据传输的安全性。
4. references
《机器学习》第3章,周志华
Good luck!