机器学习神经网络

机器学习

发布日期: 2021-09-08

更新日期: 2022-08-10

文章字数: 3.9k

阅读时长: 15 分

阅读次数:

基于numpy的实现代码传送门

循环神经网络（Recurrent Neural Network，RNN）是一种专门用于处理时间序列任务的神经网络，而自然语言就是一种典型的时间序列，所以RNN模型又多用于NLP任务。

1. 输入输出

训练输入： \[ T=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中，

$x$ 为特征域，$x_i \in \mathbb{R}^{m \times n},i =1,2,...,N$，$m$ 为时间长度，$n$ 为特征维度大小
$y$ 为标签域，$y_i \in \mathbb R^{m \times K}$ ，$K$ 为输出标签集合大小，$y_i$ 是一个二维的one-hot向量
注：序列任务的输出大致可以归为两种情况：
- 标注类任务。序列中每个元素输出一个标签，即 $y_i \in \mathbb R^{m \times K}$。
- 文本分类任务。每个序列输出一个标签，即 $y_i \in \mathbb R^{K}$ ，为了表示一致，改记为 $y_i \in \mathbb R^{1 \times K}$，即 $m=1$。

测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^{m \times n} \] 测试输出： \[ Y'=\{y'_1,\cdots,y'_{N'}\},y_i' \in \mathbb R^{m \times K} \]

2. 模型效果

上图是一个时间序列预测的demo。

图中，红线为函数 $\sin(t)$ 的关于时间 $t$ 的时间序列曲线，蓝线为使用RNN根据输入时间区间 $[t_i,t_j]$ 预测当前时间区间的函数值序列曲线

3. 基本定义

首先来看时间序列。时间序列任务在之前的笔记中已多次提及，这里再简单提及一下。例如，对于句子 我爱你 ，这就是一个序列的输入，$t_0$ 时刻输入“我”，$t_1$ 时刻输入“爱”，以此类推。

因为序列任务也属于分类任务，所以自然也可以用普通的DNN模型来完成，但效果一般都不好。DNN模型是典型的词袋模型，每个元素的输入都是独立的，这意味不同顺序的输入效果可能是一样的，例如，在DNN眼中，我爱你和 你爱我的意思是一样。

RNN的基本思想很简单，就是和众多时序模型一样，想方设法的将以往的信息加入到当前时刻的训练中。基于这个思想，RNN将上一时刻隐藏的信息（也有选择将上一时刻的输入层或输出层信息）加入到当前时刻的隐藏层中。

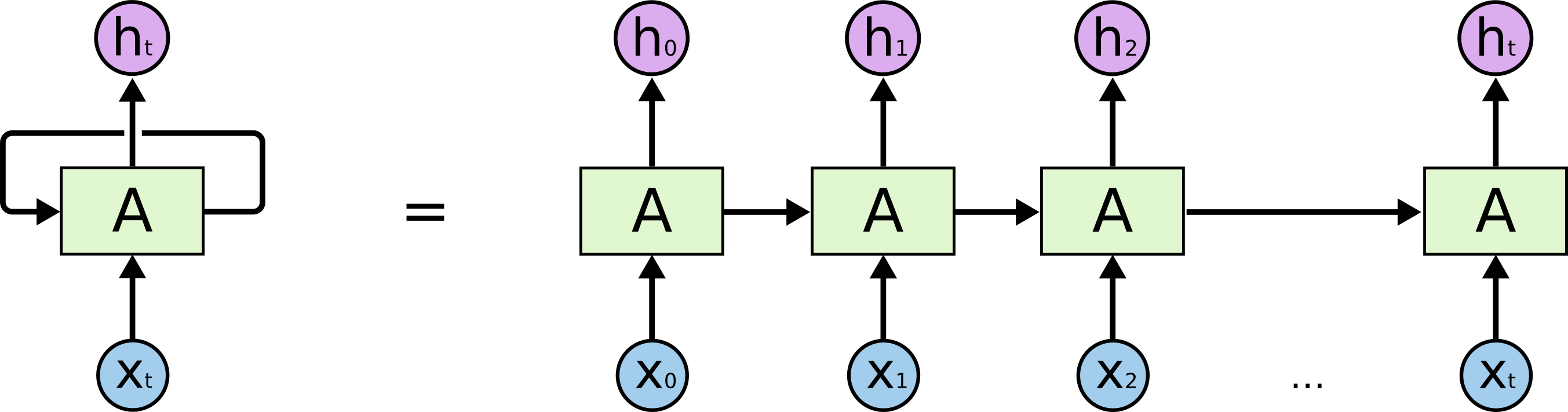
一个经典的RNN网络由输入层、循环层（Recurrent Layer）、全连接层构成，经典结构如下所示

上图中（下面为表示方便，以一个神经元向量进行表示，如果要表示整一层的权重，则用大写的矩阵表示。）

左图模型总体数据流结构图，右图是按时刻拆开后的模型结果图。（RNN模型的结构图太难表示了，以至于不得不使用这种方式进行表达）
当前时刻 $t$ 的上一层（不妨看做输入层）的神经元向量为 $x_t\in \mathbb{R}^{1 \times n}$；下一层（不妨看做输出层）的神经元向量为 $h_t\in \mathbb{R}^{1 \times n_c}$ ；当前层（即隐藏层）的神经元向量为 $s_t\in \mathbb{R}^{1 \times n_c}$
$x_t \rightarrow s_t$ 的权重和偏置分别为 $V$ 和 $b_s$ ； $s_{t-1} \rightarrow s_t$ 的权重为 $U$ ； $h_t \rightarrow o_t$ 的权重和偏置分别为 $W$ 和 $b_h$ ；$s_t \rightarrow h_t$ 还可以做若干线性变换的操作，这里为了推导方便，直接使 $h_t = s_t$
为了表示方便，记 $\sigma(x) = \text{sigmoid}(x), \phi(x) = \tanh(x)$

3.1. 输入层

总输入是一个长度为 $m$ 的时间序列，每个时刻的输入元素向量长度为 $n$ 。

对于NLP任务，输入层后面一般还要接一个embedding layer，将词的one-hot编码转为向量编码（这一步的作用在之前的预训练-word2vec这篇笔记中有所分析，这里也不再赘述），但一般会将embedding layer也包含进输入层中。

输入层输出维度：$\{m \times n\}$

3.2. 循环层

3.2.1. 前向传递

当前时刻隐藏层 $ s_t$ 的输入流有两个：当前时刻的输入层 $x_t$ 及上一时刻的隐藏层 $s_{t-1}$ ，所以从输入到隐藏的传递公式为 \[ s_t = \phi (Vx_t + Us_{t-1} + b_s) \] 上面表达式实际上是一个递归的加性函数，对其展开可得 \[ s_t = \phi (Vx_t + Us_{t-1} + b_s) \\ s_{t-1} = \phi (Vx_{t-1} + Us_{t-2} + b_s) \\ \cdots \\ s_0 = \phi (Vx_0 + b_s) \] 一般来说，循环层激活函数都是用tanh函数。下面来分析一下为什么一般不选用sigmoid函数和tanh函数

sigmoid函数和tanh函数曲线是很相似的。通常观点认为，sigmoid函数是非中心对称函数，而tanh是中心对称的，在0附近梯度大，收敛速度快，所以选用tanh函数比sigmoid函数要优；

relu函数的正方向的导数为1，对梯度没有衰减，极容易造成梯度爆炸的问题，所以尽量避免在NLP中使用relu函数。

当然，如果可以找到一个合适的初始值，sigmoid和relu都是可以使用的。例如，iRNN就采用了relu函数。

输出输入维度变化：$x \rightarrow h : \{ m \times n \} \rightarrow \{ m \times n_c\}$

3.2.2. 反向传递

RNN的反向求导用（Backpropagation Through Time）算法

需要求3个变量，所以需要给出4个梯度表达式 $\frac{\partial s_t}{\partial x_t},\frac{\partial s_t}{\partial V},\frac{\partial s_t}{\partial U}, \frac{\partial s_t}{\partial b}$

$\frac{\partial s_t}{\partial x_t}$

对 $s_t$ 递归式展开，只保留包含 $x_t$ 的项，发现 \[ s_t \propto \phi(Vx_t) \] $x_t$ 不包含递归项中，所以直接求梯度可得 \[ \frac{\partial s_t}{\partial x_t} = V\cdot \phi'(Vx_t) \]
$\frac{\partial s_t}{\partial V}$

对 $s_t$ 递归式展开，发现V在递归项中

令 $g_t = Vx_t + Us_{t-1} + b_s$ ，则 $s_t=\phi(g_t),\frac{\partial s_t}{\partial g_t} = \phi'(g_t) = 1 - \phi(g_t)^2$

对其递归求梯度得 \[ \frac{\partial s_t}{\partial V} = \frac{\partial s_t}{\partial g_t} \frac{\partial g_t}{\partial V} = \phi'(g_t) (x_t + (\frac{\partial s_{t-1}}{\partial V})^T\text{diag}(U))^T \\ \frac{\partial s_{t-1}}{\partial V} = \phi'(g_{t-1}) (x_{t-1} +(\frac{\partial s_{t-2}}{\partial V})^T\text{diag}(U))^T \\ \cdots \\ \frac{\partial s_{0}}{\partial V} = \phi'(g_0) x_{0} = \phi'(Vx_0 + b_s)x_0^T \]
$\frac{\partial s_t}{\partial U}$

类似的，递归求导得 \[ \frac{\partial s_t}{\partial U} = \frac{\partial s_t}{\partial g_t} \frac{\partial g_t}{\partial U} = \phi'(g_t) (s_{t-1} + (\frac{\partial s_{t-1}}{\partial U})^T\text{diag}(U))^T \\ \frac{\partial s_{t-1}}{\partial U} = \phi'(g_{t-1}) (s_{t-2} + (\frac{\partial s_{t-2}}{\partial U})^T\text{diag}(U))^T \\ \cdots \\ \frac{\partial s_{1}}{\partial U} = \phi'(g_1)s_0^T \] 值得注意的是，在 $t=0$ 时刻，U不需要更新参数
$\frac{\partial s_t}{\partial b}$

类似的，递归求导得 \[ \frac{\partial s_t}{\partial b_s} = \frac{\partial s_t}{\partial g_t} \frac{\partial g_t}{\partial b_s} = \phi'(g_t) (1 + U\frac{\partial s_{t-1}}{\partial b_s}) \\ \frac{\partial s_{t-1}}{\partial b_s} = \phi'(g_{t-1}) (1 +U\frac{\partial s_{t-2}}{\partial b_s}) \\ \cdots \\ \frac{\partial s_{0}}{\partial b_s} = \phi'(g_0) = \phi'(Vx_0 + b_s) \]

从上面的推导中可以看出，当前时刻的梯度更新包含以往所有时刻的梯度，从最优化的角度来看，这会使RNN比一般的DNN更容易出现梯度消失或爆炸的情况。

为了解决上述问题，BPTT会限定一个阈值 $\tau$ ，仅回溯之前 $\tau$ 个时刻的梯度值，这种思想类似于常见n-gram做法。

3.3. 全连接层

3.3.1. 前向传递

而隐藏层到输出层的数据流跟普通DNN模型是完全一样的，即 \[ o_t = a(Wh_t + b_h) \]

激活函数的选择，二分类任务用sigmoid，多分类任务用softmax即可（一些回归型任务可以不使用激活函数）。

标注类型任务

传统做法是每一个时刻输出一个预测值，但这样只能串行计算，RNN的运行效率并不高。

很多时候为了能够并行运算，每个时刻的输入后并不会立刻进行反向传递更新参数，而是等到所有时刻都输入后，再进行反向传递，此时反向传播时的损失值为所有时刻的损失值之和（或均值），且输入必须是等长序列。

输入输出维度变化：$h \rightarrow o : \{ m \times n_c \} \rightarrow \{m \times K\}$
文本分类任务

一个序列全部输入后再输出一个预测值，此时反向传播时的损失值为所有时刻的损失值之和（或均值）

输入输出维度变化：$h \rightarrow o : \{ m \times n_c \} \rightarrow \{1 \times K\}$

3.3.2. 反向传递

反向推导过程参考之前的神经网络笔记，略。

4. 一些改进

4.1. LSTM

之前提及设置阈值 $\tau$ 的RNN网络，这种做法由于只保留最近 $\tau$ 个时刻的信息，会使RNN变成短期记忆网络，在一些情况下需要关联过去较长时刻的信息，例如，无主语句子。如果保留过去全量的信息，又会造成梯度消失和爆炸等问题。

为了解决上述问题，提出了长短记忆单元（Long Short-Term Memory Unit，LSTM）

4.1.1. 前向传递

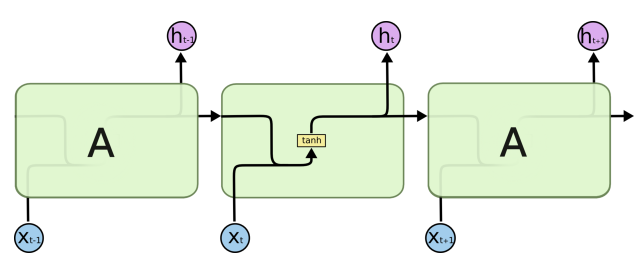
首先给出LSTM的结构图

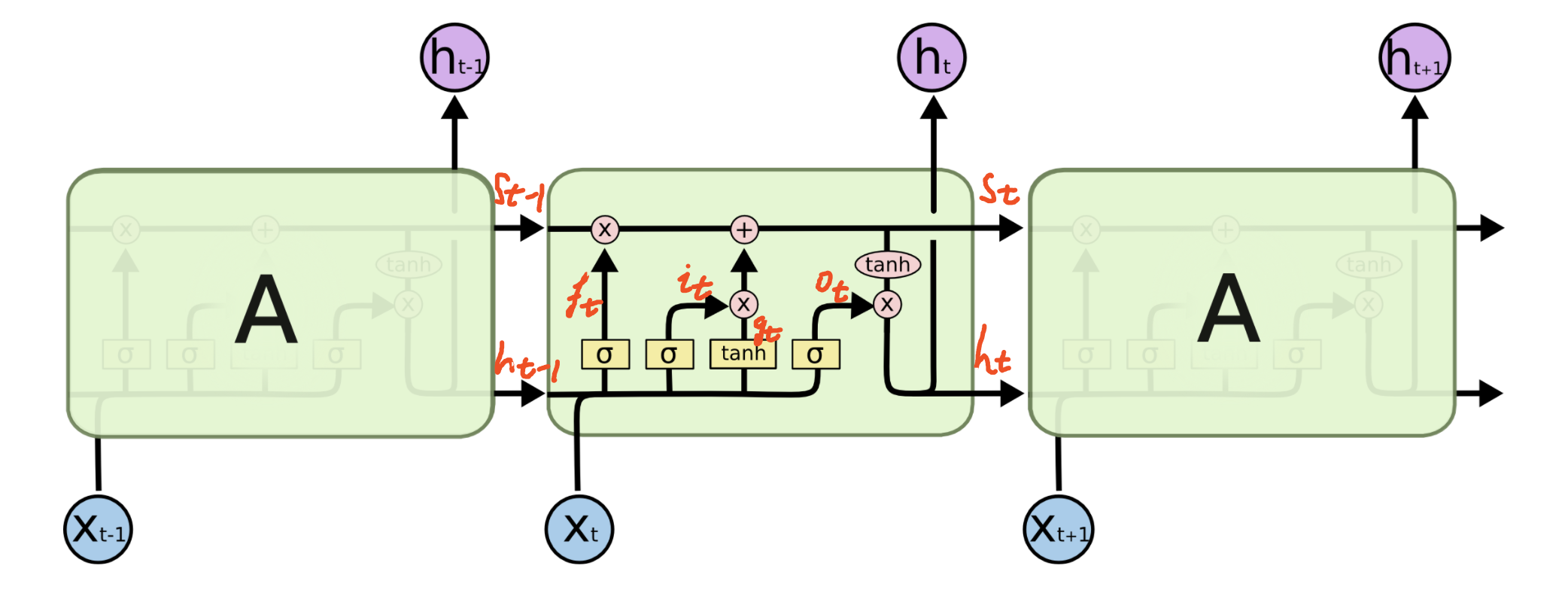
要看明白这张图需要花费一点时间，一个技巧是看操作符，根据操作符前后的输入输出流给出对应的表达式。

图中，$\sigma,\tanh$ 表示激活函数，$\times,+$ 分别表示矩阵的Hadamard积（矩阵对应元素相乘）和矩阵加法。

按照操作符给出各数据流的表达式 \[ \begin{aligned} i_t &=\sigma\left(W_{i} x_{c}(t)+b_{i}\right) \\ f_t &=\sigma\left(W_{f} x_{c}(t)+b_{f}\right) \\ o_t &=\sigma\left(W_{o} x_{c}(t)+b_{o}\right) \\ g_t &=\phi\left(W_{g} x_{c}(t)+b_{g}\right) \\ s_t &=g_t \odot i_t+s_{t-1} \odot f_t \\ h_t &=o_t \odot \phi(s_t) \end{aligned} \] 其中，$\odot$ 表示Hadamard积，$x_c(t) = [x_t,h_{t-1}]$

比较LSTM和RNN的差异。

首先，LSTM是一个综合了原先RNN的输入层、循环层和输出层的结构，像这种综合多个层的结构称为单元（Unit）。$s_t$ 是单元的权重

$i_t,f_t,o_t$ 是在原先循环层的基础上新增的数据流，称为门控系统，分别称为输出门，遗忘门、输出门，是LSTM的精髓所在；$i_t$ 控制 $x_t \rightarrow s_t$ 的数据流，$ f_t$ 控制 $s_{t-1} \rightarrow s_t$ 的数据流， $ o_t$ 控制 $s_t h_t $ 的数据流；$g_t$ 是细胞的缓存的权重。

$i_t,f_t,o_t$ 这三个门结构和作用都相似，以 $i_t$ 为例进行分析。

$i_t$ 受到当前时刻输入 $x_t$ 和过去时刻隐层输出 $h_{t-1}$ 综合作用；激活函数选用sigmoid函数，取值区间为 $[0,1]$ ，这表示输出的衰减程度（或者是信息的保留程度），值为0时表示完全丢弃，值为1时表示完全保留。

将门控与对应的输入流做Hadamard相乘，意味着当前时刻输入在上一时刻隐层的输出的影响下，如果想要对模型的最终决策的占比较大，则门控的衰减应该低，反之则应该较高（当然门控的衰减率会由网络自主学习获得），即达到选择性记忆的功能，亦即“长/短”记忆模型。

遗忘门能决定需要保留先前步长中哪些相关信息，输入门决定在当前输入中哪些重要信息需要被添加，输出门决定了下一个隐藏状态。

故LSTM的本质通过只记忆重要输入信息，减少总体序列记忆长度，从而既能最大程度保留序列整体信息，又能减轻梯度消失和爆炸的问题。

4.1.2. 反向传递

由于需要这一层的变量较多，这里就不一一具体给出，自行如法炮制即可

注：

Hadamard积的求导 \[ d (U \odot V) = d U \odot V + U \odot dV \]

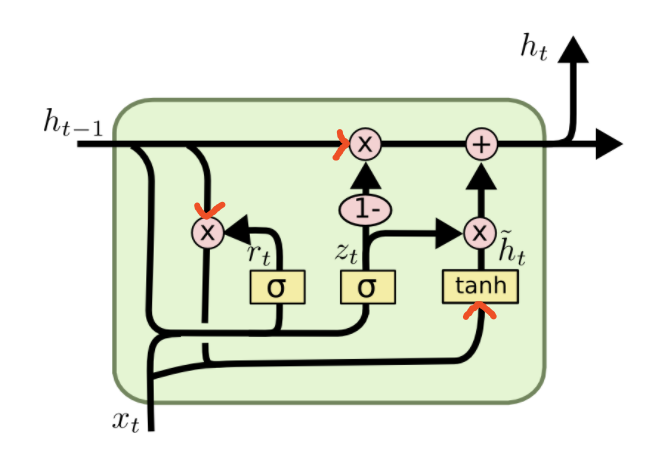
4.2. GRU

4.2.1. 前向传递

由于LSTM的参数较多，训练效率低，门控循环单元（Gated Recurrent Unit，GRU）在LSTM的基础上，取消了单元权重，并将三个门精简到两个门。

GRU结构图

仍然按照操作符给出各数据流的表达式 \[ \begin{aligned} z_{t} &=\sigma\left(W_{z} \cdot x_c(t)\right) \\ r_{t} &=\sigma\left(W_{r} \cdot x_c(t)\right) \\ \tilde{h}_{t} &=\phi \left(W \cdot\left[r_{t} \odot h_{t-1}, x_{t}\right]\right) \\ h_{t} &=\left(1-z_{t}\right) \odot h_{t-1}+z_{t} \odot \tilde{h}_{t} \end{aligned} \] 其中，$r_t,z_t$ 分别叫做重置门和更新门，$r_{t}$ 是 $x_t \rightarrow h_t$ 的数据流，$z_{t}$ 是 $h_{t-1} \rightarrow h_t$ 的数据流；$\tilde{h}_{t}$ 是隐层的缓存权重

对比LSTM

GRU取消了单元状态 $s_t$ ，所以其需要训练的参数大大减少；
重置门 $r_t$ ，顾名思义，其对上一时刻的隐层输出 $h_{t-1}$ 进行了重置，再混合当前时刻的输入 $x_t$ ，形成当前时刻的隐层的输入 $\tilde{h}_{t}$
更新门 $z_t$ ，分别用 $z_t$ 和 $1-z_t$ 替代LSTM中 $i_t$ 和 $f_t$ 。这是一个非常巧妙的设计。 $z_t$ 和 $1-z_t$ 是互为关联的。当输入 $\tilde{h}_{t}$ 以 $z_t$ 的权重进行保留时，则会对过去时刻的隐层 $h_{t-1}$ 以 $z_t$ 的权重进行遗忘。这种做法，我们在计算信息熵的时候用到过。

4.2.2. 反向传播

略。

4.3. Bi-LSTM

4.3.1. 前向传递

一般来说，像自语言这种序列问题，当前时刻的输入会与过去时刻与未来时刻的输入都有关，但普通LSTM只具有前溯性，为了使其具有后溯性，在LSTM的基础上提出了双向循环神经网络（Bi-directional Long Short-Term Memory，Bi-LSTM）

（网上找到的资料都千篇一律-_-||）

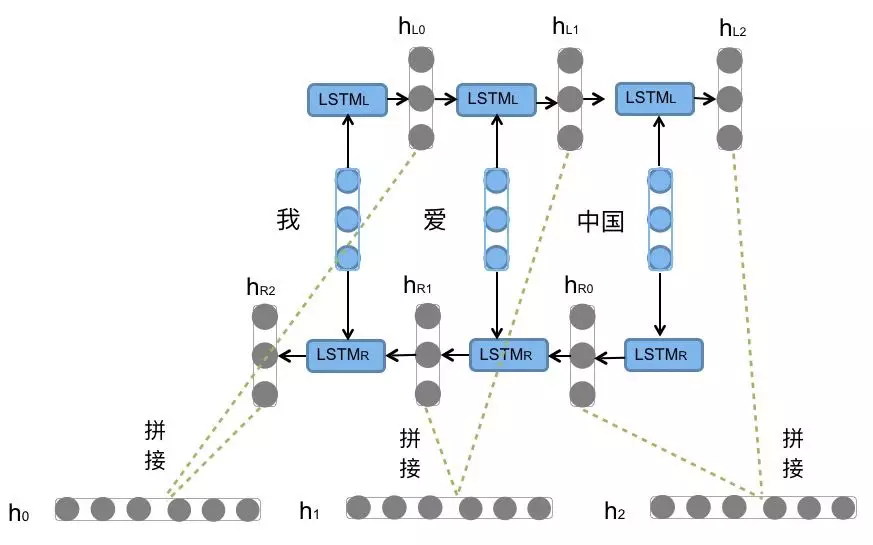
上图中，Bi-LSTM由两个参数不共享的LSTM构成。前向传播时分为两个数据流向，一个是从 $t_0$ 时刻开始输入至 $t_T$ 时刻结束输入的前向数据流；一个是从 $t_T$ 时刻开始输入至 $t_0$ 时刻结束输入的后向数据流。这两个数据流向可以并行计算。每一时刻的两个LSTM的输出不进行预测及反向传播，等到所有时刻都输出完成后，对每一时刻的两个LSTM的输出进行拼接，此时再统一进行预测和反向传播。