基于numpy的实现代码传送门
1. 相关含义
特征缩放(Feature Scaling),是一种对输入或输出数据进行调整的方法。
出于习惯和中文翻译,一般也被称为归一化(normalization)或标准化(standardization),至于这些叫法之间区别,知乎上也有相关的问题对其进行讨论。
一个普遍的观点是,归一化、标准化、中心化(mean normalization)等等都是特征缩放中的一个具体方法,更加具体的,归一化对应下面的min_max方法(更加准确的,这个时候的归一化应为min-max normalization,只不过出于习惯简称为normalization),中心化对应下面的mean方法,标准化对应下面的z_scores方法。
但上面的各种说法只包含的线性变换,至于非线性变换就没有一个具体的叫法了。再者,实际上上面的各种叫法并没有一个很明确的区分。归一化,即将数据缩放到1个单位范围内;中心化,即将数据缩放到以坐标原点为中心点;标准化,即将数据缩放至标准分布(不一定是标准正态分布)。可以看出,上面的各种做法都是存在交集的。
所以日常交流中,一般都对上面的说法进行混用,并不会做很严格的咬文嚼字般的区分,因为大家都默认指的是同一件事情——对数据进行特征缩放。而我一般上习惯将其都称为特征变换。
上面提到,特征变换一般分为线性变换和非线性变换,下面来看下这两种变换的差异。
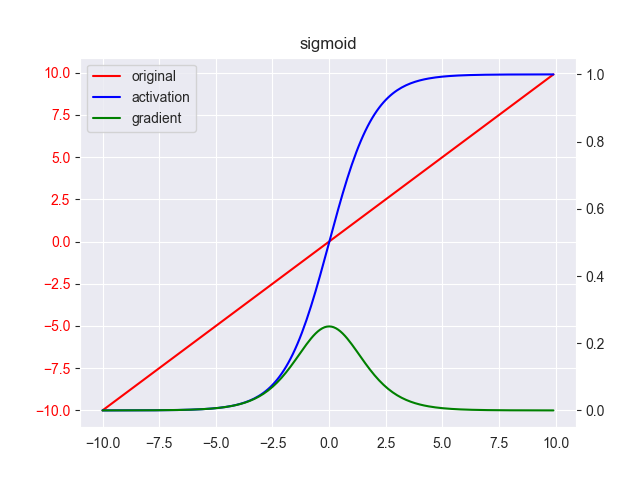
线性变换本质上是对数据进行缩放和平移,所以不改变数据的分布情况,主要是对各个特征维度无量纲化,一般用来消除数据横向差异(即特征间差异)。至于这样做的目的,一种普遍的观点是算法进行梯度求解时,将椭圆形状的曲折求解变成圆形的笔直求解,从而得到更好的收敛效果,如下图所示


还有一种观点是认为其将目标函数的Hessian矩阵的条件数变小,从而有更好的收敛性质,总之,最终的结果是使训练的速度变快、效果更好。
非线性变换,本质是上是对数据进行平滑处理,所以会拉近样本间的距离,一般用来消除数据纵向差异(样本间),主要用于减轻奇异数据对预测结果的影响,具有一定的噪声抗干扰能力,但由于会改变数据的分布情况,所以一般对使用的场景要求很苛刻。
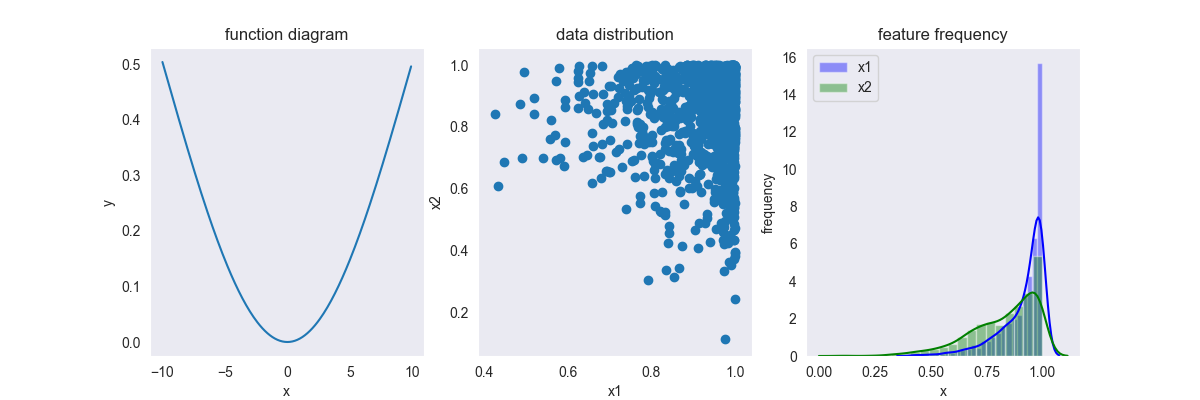
2. 原始数据
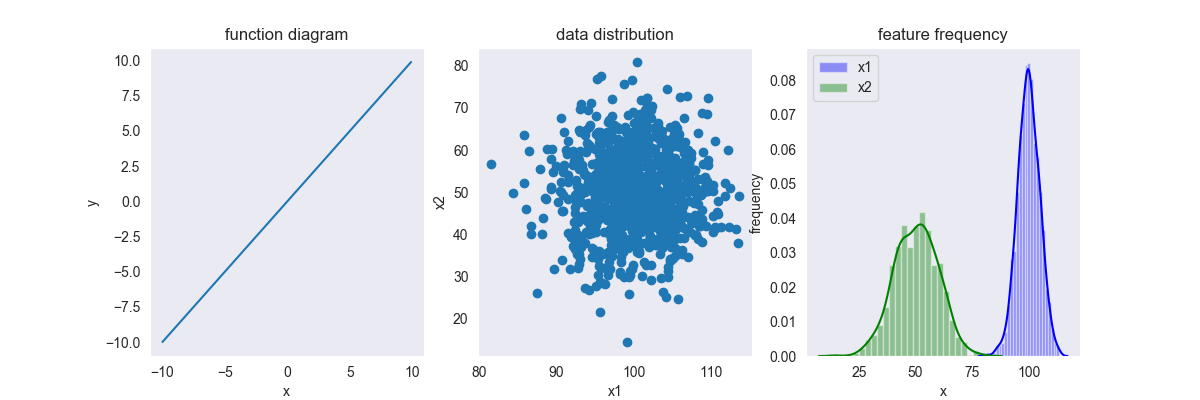
第一个图是缩放方法关于 \(f(x) = x\) 的函数图像,后面两个图是样例数据的分布图像,假设 \(x\) 具有两个特征维度,那么,第二个图像就是 \(x\) 关于特征超平面的数据分布情况,第三个图为 \(x\) 关于每个特征的直方图和核函数密度估计图。
我们假设数据的每个维度都服从正态分布,可以看得出两个维度的均值是不一样的。你可以假设两个维度的量纲是不一样的,例如,x1为身高(但均值为100的身高也太矮了吧,hhh),x2为体重等
3. 线性变换
3.1. Min_max
\[ y = \frac{x-\min(x)}{\max(x)-\min(x) } \]
其中,\(x \in [-\infty, +\infty],y \in [0,1]\)
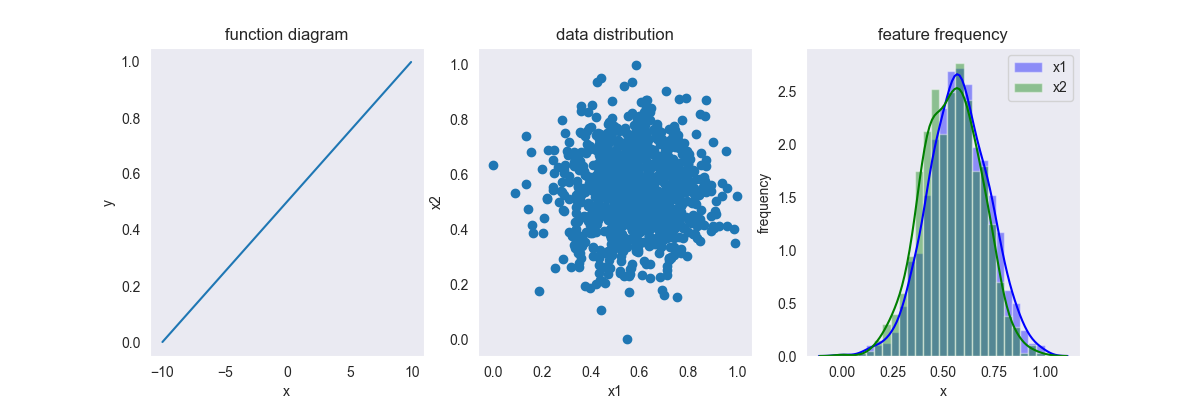
这种变换是用得最多的变换,如果事先不知道数据的分布情况,建议先对数据进行归一化处理,再根据预测结果决定是否采用其他变换方法。
3.2. Mean
\[ y = \frac{x-\mu}{\max(x)-\min(x) } \]
其中,\(x \in [-\infty, +\infty],y \in [-1,1]\)
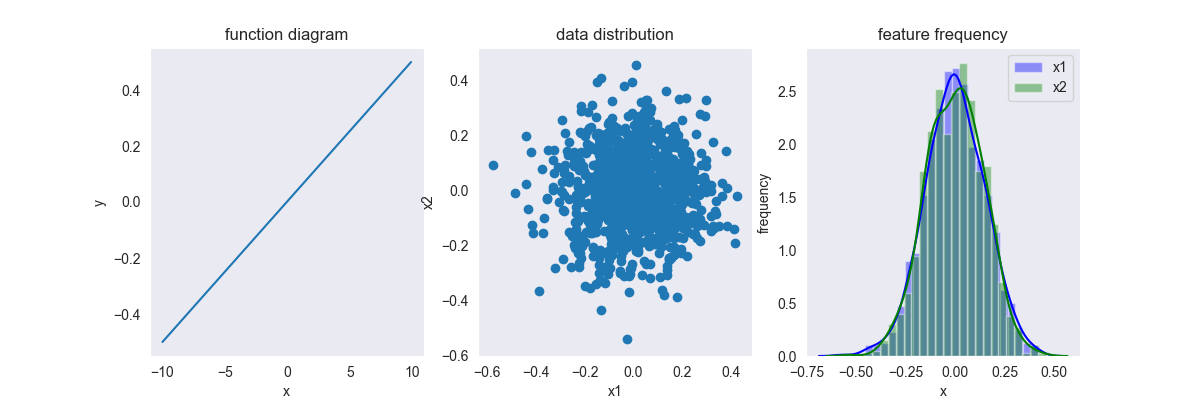
3.3. Z_score
\[ \text{z-score}(x) = \frac{x-\mu}{\sigma} \]
其中,\(x \in [-\infty, +\infty],y \in [-\infty, +\infty]\)
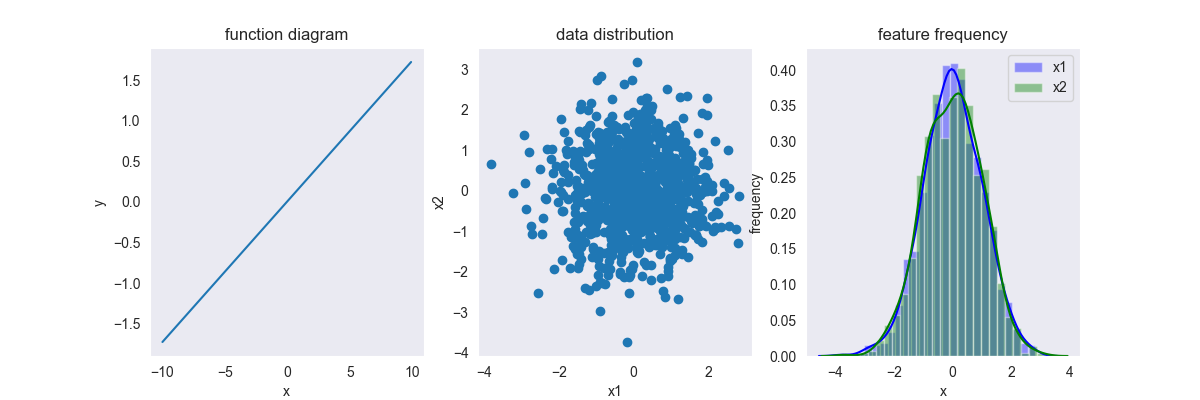
PS:标准化不会改变数据的分布情况,变换前是泊松分布,变换后还是泊松分布,只不过变换后每个特征维度的均值变为0,方差变为1
4. 非线性变换
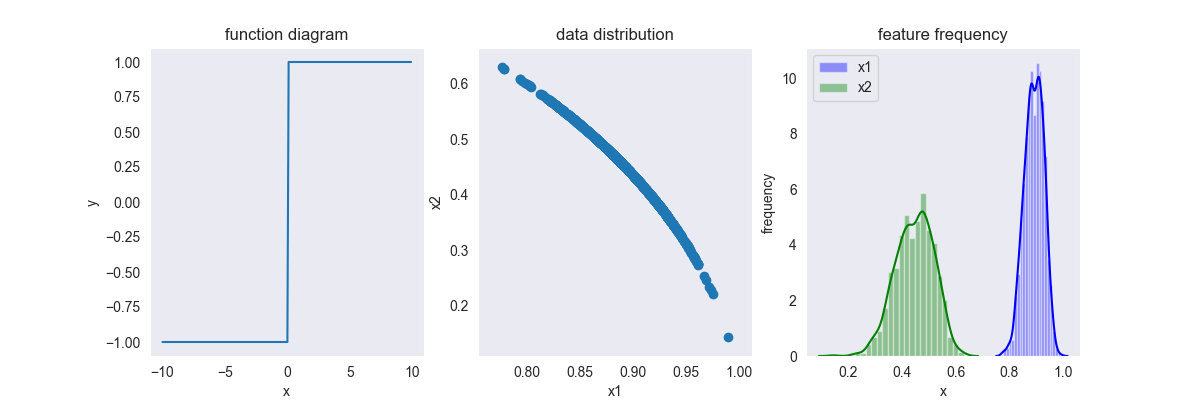
4.1. Vec
使每个样本缩放至一个单位圆上 \[ f(x) = \frac{x}{||X||} \] 其中,\(x \in [-\infty, +\infty],y \in [-1,1]\)
4.2. Log
\[ f(x) = \frac{\lg(x)}{\lg \max(x)} \]
其中,\(x \in [0, +\infty],y \in [-1,1]\)
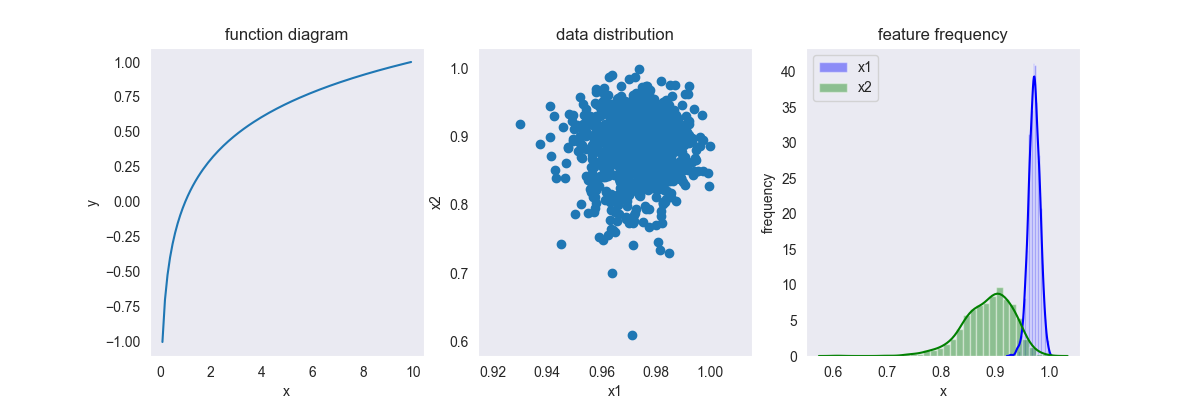
从函数图像中可以看出,中间有一段跨度很大的平滑区,所以该变换主要用于平滑样本间量级差异很大的数据
变换后,数据分布整体往右移,即趋向于1
PS:改变换可以以任意值作为对数的底,并不是一定只能使用以10为底的对数
4.3. Arctan
\[ f(x) = \frac{2\arctan(x) }{\pi} \]
其中,\(x \in [-\infty, +\infty],y \in [-1,1]\)
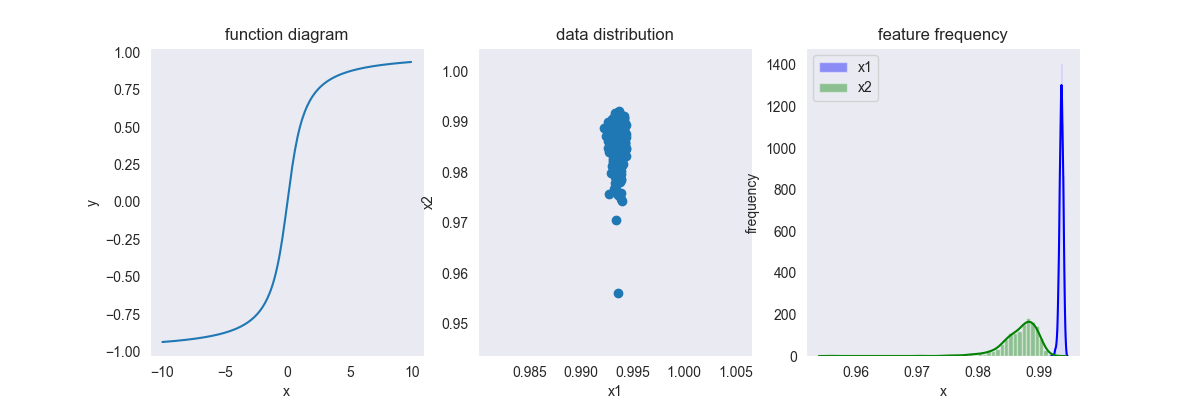
这是一种平滑方法,对比log变换,其可以对负值进行平滑处理,而且其平滑区域极大,基本上把所有量级的数据平滑至一个非常相近的区域内
4.4. Binarizer
将数据变成0-1分布 \[ f(x) = \left \{ \begin{array}{ll} 0 & ,x \geq \theta \\ 1 & ,x < \theta \end{array} \right . \] 其中,\(x \in [-\infty, +\infty],y \in \{0,1 \}\),\(\theta\) 划分阈值,一般取各个维度的均值
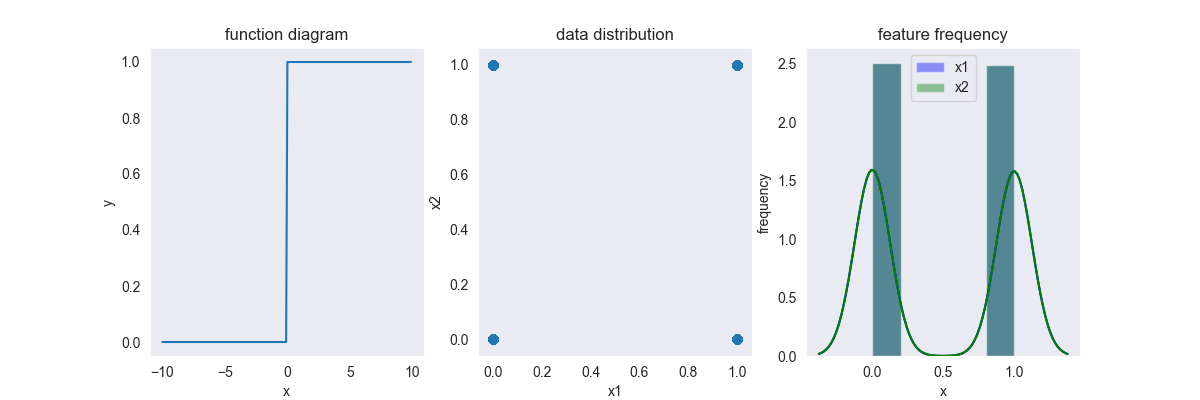
这种变换一般用于对标签域进行变换,与此类似的变换还有 \(\text{sign}(x)\) 变换
4.5. Fuzzy
\[ f(x) = \frac{1}{2} + \frac{1}{2} \sin \frac{\pi}{(\max(x) - min(x))(x - 0.5(\max(x) - min(x)))} \]
其中,\(x \in [-\infty, +\infty],y \in [0,1]\)
由于是很久之前实现的方法,当时没有及时的记录下来,现在也没搜到相关的介绍,所以目前暂时无法追溯其出处,也不知道这个方法准确用途,只能从名字上大概判断这是一个用来模糊特征的函数。
5. references
https://blog.csdn.net/weixin_36604953/article/details/102652160
https://www.cnblogs.com/jasonfreak/p/5448385.html
Farewell~