基于numpy的实现代码传送门
1. 基本定义
LVQ聚类算法也是一种原型聚类,与Kmeans算法类似,也是选择向量点作为原型,以距离作为聚类标准。但与Kmeans自由随机初始中心点不一样的是,LVQ需要在先验标签值的指导下进行随机初始化。
对于这个算法,我们会产生一些疑问。
首先,既然已经有标签数据,那么为什么还要进行聚类呢?
对于这个问题,我的看法是,我们输入的先验标签数据不一定是绝对真实的取值,可能是其他分类器输出的结果,可能是片面的、残缺的,需要靠聚类进行矫正和修补。(可以将先验知识当做一个约束值,该算法相当于在已知的约束条件下求解最最优值的过程)
对于矫正作用,由于输入的只有标签值,需要靠聚类进行类别边界的拟合;对于修补作用,由于LVQ聚类算法允许聚类的簇比输入的标签的类别多,这意味着一个类别可以被重新分割成多个类别。
其次,标签值是必须的吗?
一种说法是标签值是非必须的,如果没有先验的标签值,可以输入随机的标签值。
我不太认同这种做法。因为标签值是一种约束,随机的约束即相当于没有约束,那么LVQ算法其实就退化为一般的聚类的算法,甚至更加严重,随机会使得系统更加混沌,算法会因为错误的指导给出效果更差的答案。
所以我更偏向于将其归为半监督的聚类算法。
2. 输入输出
Input:
输入训练集 \[ T=\{(x_1,y_1), (x_2,y_2),...,(x_N,y_N)\} \] 其中,\(x_i \in \mathbb{R}^n,y_i \in \{1,2,...,m\},i =1,2,...,N\),\(x_i\) 为特征域,\(y_i\) 为标签域
需要划分的类簇个数 \(k\)
Output:
样本空间中每个点的预测类别 \[ Y'=\{y'_1,y'_2,...,y'_{N}\},y'_i \in \{0,1,...,k\} \] 类簇集合 \[ C=\{C_1,C_2,...C_k\},C_i=\{x \in X | y = y_i \} \]
3. 模型效果
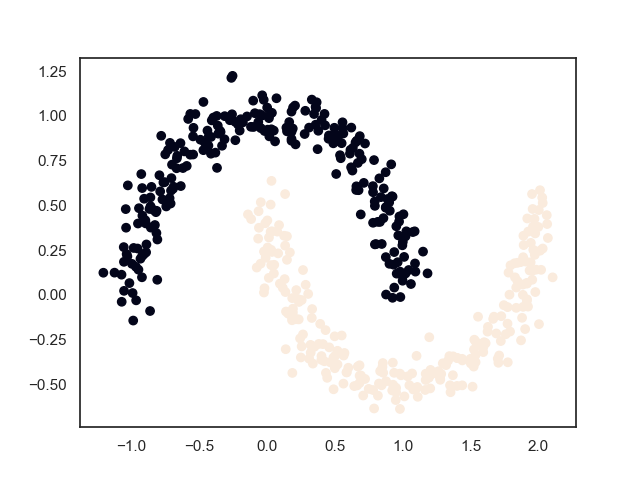
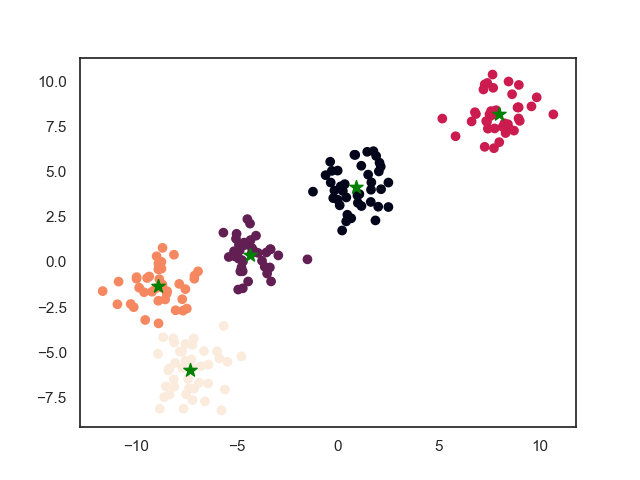
图中,初始输入:左上角两团归为一类,中间一团归为一类,右下两团归为一类。输入需要聚类的簇数为5。聚类后左上角一类被拆成两类,右下一类也被拆成两类。整个聚类过程可以看做各自类别中分别再进行聚类。
最终结果如下所示
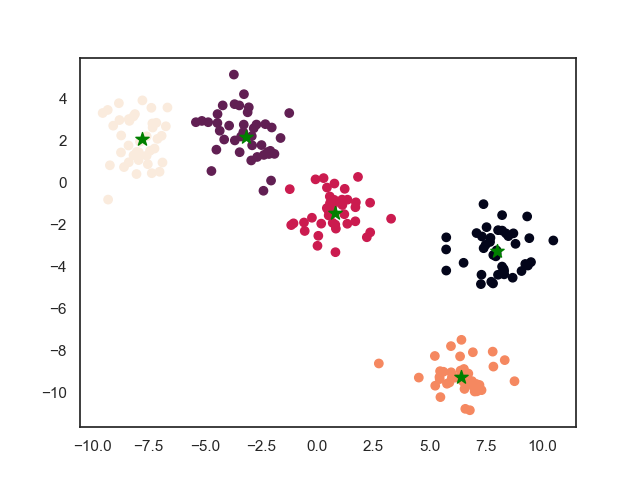
4. 模型推导
4.1. 基本方法
计算每个簇的向量原型点原型向量集合 \(\{p_1,...,p_k\}\)
模型函数为 \[ f(x) = \arg \min_{0 \leq i \leq k} \{||x - p_i||^2\} \]
4.2. 学习算法
与Kmeans算法类似,使用启发式的学习算法。
Init:
- 循环从每个类别中随机选择一个点作为原型向量,如果如果类别数小于聚类数,即 \(k>m\) ,则重新从第一个类别中继续选取。得到原型向量集合 \(\{p_1,...,p_k\}\) ,每一个原型向量的类别标签 \(\{t_1,,...,t_k\}\) (注意与簇类标签的区别)
- 学习率 \(\eta \in (0,1)\)
Repeat:
- 从样本空间中随机选取一个样本 \((x_j,y_j)\)(为什么这里是随机选取而不是循环选取,西瓜书上没有解释,为了方便实现,这里按照循环选取的方式进行)
- 计算与 \(x_j\) 与距离最近的原型向量, \(i=\arg \min_{1 \leq i \leq k} \{d_{ij}=||x_j-p_i||^2\}\)
- 如果 \(y_j=t_i\),则说明预测成功,则原型向量向该点靠近,即 \(p_i \leftarrow p_i + \eta (x_j - p_i)\)
- 如果 \(y_j=t_i\),则说明预测失败,则原型向量向该点远离,即 \(p_i \leftarrow p_i - \eta (x_j - p_i)\)
Until: 原型向量的变化值小于 \(\delta\) 或达到最大迭代次数
5. references
《机器学习》9.4.2节,周志华
Good night~