机器学习聚类算法

机器学习

发布日期: 2020-11-25

更新日期: 2022-08-10

文章字数: 830

阅读时长: 3 分

阅读次数:

基于numpy的实现代码传送门

K均值（Kmeans）算法应该算是一个入门级的聚类算法。

Kmeans属于硬聚类、原型聚类。

聚类可分为硬聚类和软聚类，如果一个点只能归属于一个类簇，则为硬聚类，如果一个点可以归属于多个类簇，则为软聚类。实际应用多以硬聚类为主，后面提及的聚类算法如无特殊说明，都表示硬聚类。

原型聚类也称作“基于原型的聚类”，此类算法假设聚类结构可以通过一组原型刻画，在现实任务中极为常见。（“原型”是指样本空间中具有代表性的点），所以原型聚类一般可以用一个可表达的系统函数进行描述，这意味着原型聚类模型训练完成后可以当成一个分类器

1. 输入输出

Input:

样本空间 \[ X= \{x_1, x_2, ..., x_N\},x_i \in \mathbb{R}^n \] 需要划分的类簇个数 \(k\)

Output:

样本空间中每个点的预测类别 \[ Y=\{y_1,y_2,...,y_{N}\},y_i \in \{0,1,...,k\} \] 类簇集合 \[ C=\{C_1,C_2,...C_k\},C_i=\{x \in X | y = y_i \} \]

2. 模型效果

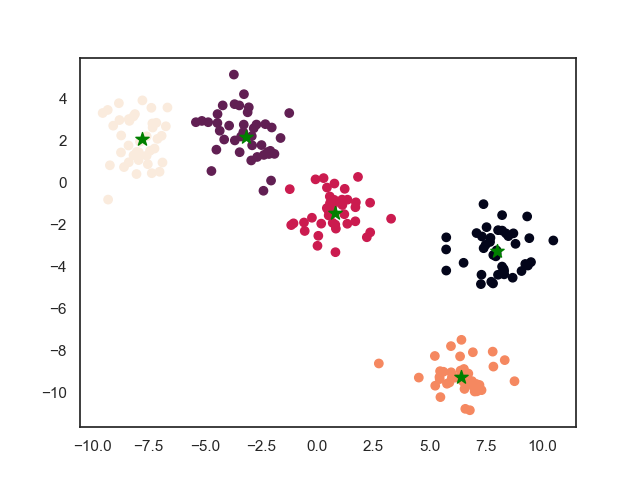
2.1. 训练效果

2.2. 最终结果

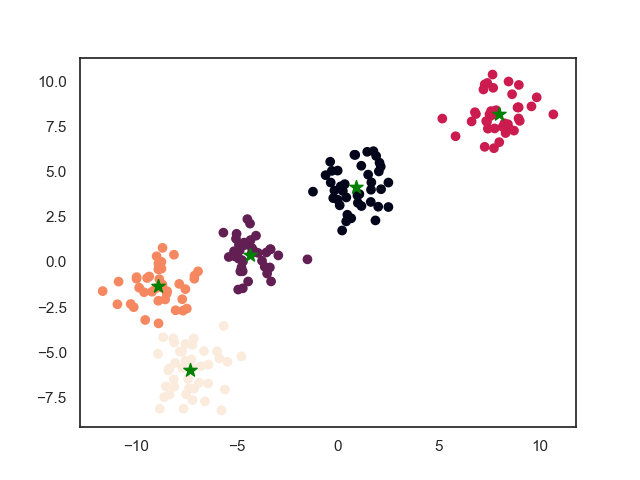
3. 模型推导

3.1. 基本方法

选取每个簇的中心点作为原型点

记簇 \(C_i\) 的中心点为 \[ u_i = \frac{\sum_{j=1}^N x_j \cdot I(y_j=i) }{\sum_{j=1}^N I(y_j=i)} \] 模型函数为 \[ f(x) = \arg \min_{0 \leq i \leq k} \{||x - u_i||^2\} \]

3.2. 学习策略

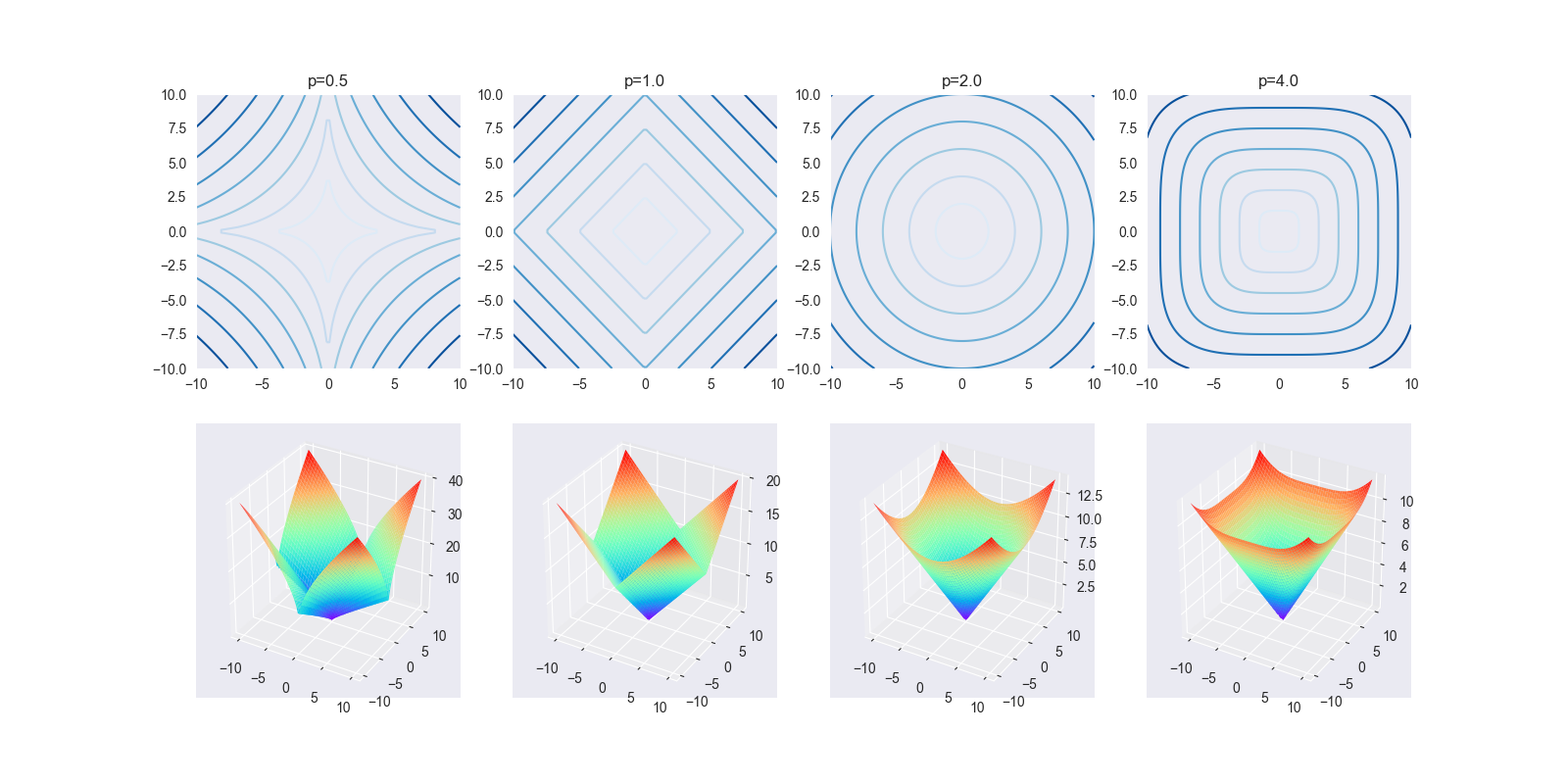
损失函数为 \[ L(C) = \sum_{i=1}^k \sum_{x_j \in C_i} ||x_j - u_i|| ^ 2 \] \(L(C)\) 也称为能量，表示相同类中的样本的相似程度

3.3. 学习算法

模型的最终问题为 \[ \min_C L(C) = \min_C \sum_{i=1}^k \sum_{x_j \in C_i} ||x_j - u_i|| ^ 2 \] 但是这个问题很难直接求解，因为 \(u_i\) 并不确定，而 \(u_i\) 的确定又依赖于 \(x_j\)，\(x_j\) 的确定又依赖于 \(u_i\) ，实际上是一个NP难的问题，所以一般采用启发式的求解算法，即算法一开始先假设各个簇的中心点 \(u_i\) ，再通过不断迭代求解。

下面给出求解的过程。

Init: 随机取样本中间的 \(k\) 个点作为中心点，即 \(U=\{u_1,...,u_k\}\)

Repeat:

重新为每个样本分配类标签：\(y_j = \arg \min_{0 \leq i \leq k} \{||x_j - u_i||^2\}\)
重新计算样本中心： \(u_i = \frac{\sum_{j=1}^N x_j \cdot I(y_j=i) }{\sum_{j=1}^N I(y_j=i)}\)

Until: 中心点不再发生变化