基于numpy的实现代码传送门
1. 基本定义
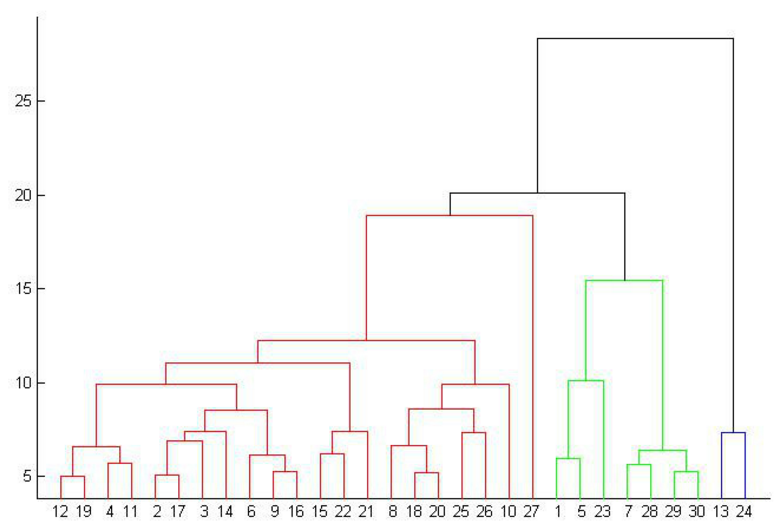
层次聚类(hierarchical cluster)在不同层次对样本进行划分,从而形成树状的聚类结构。如下所示
层次聚类一般分为聚合的(agglomerative)或自下而上(bottom-up)聚类、分裂(divisive)或自上而下(top-down)聚类。
聚合的聚类一开始将每个样本看做一个簇,然后不断将簇间距离最近的两个簇合并成一个簇;分裂的聚类一开始将所有的样本看做一个簇,然后将簇中距离最远的样本分到两个簇中,最终一个簇分裂成两个簇。
两种方法的本质思想是一样的。下面以聚合的聚类为例进行介绍。
按照合并的标准又分为:如果取最小距离为单链接算法;取最大距离为全链接算法;取平均距离为均链接算法。
2. 输入输出
Input:
样本空间 \[ X= \{x_1, x_2, ..., x_N\},x_i \in \mathbb{R}^n \] 需要划分的类簇个数 \(k\)
Output:
样本空间中每个点的预测类别 \[ Y=\{y_1,y_2,...,y_{N}\},y_i \in \{0,1,...,k\} \] 类簇集合 \[ C=\{C_1,C_2,...C_k\},C_i=\{x \in X | y = y_i \} \]
3. 模型效果
3.1. 训练效果
从上面的聚类过程中可以看出,层次聚类算法的聚类过程具有“雨后春笋”的特点,不断将距离最近的两个样本归为同类,颇有“星星之火,可以燎原”之势。
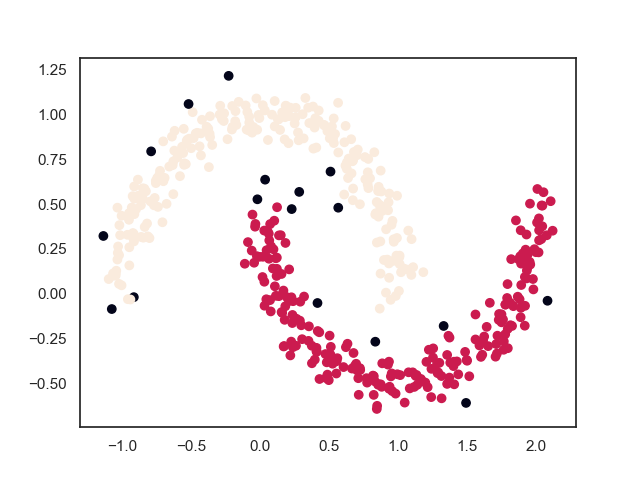
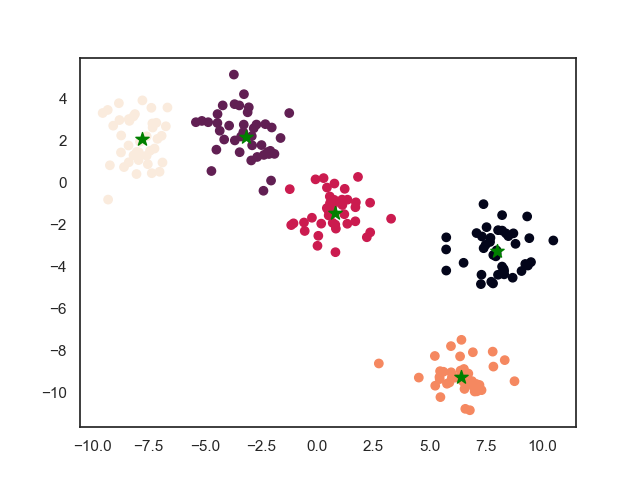
3.2. 最终结果
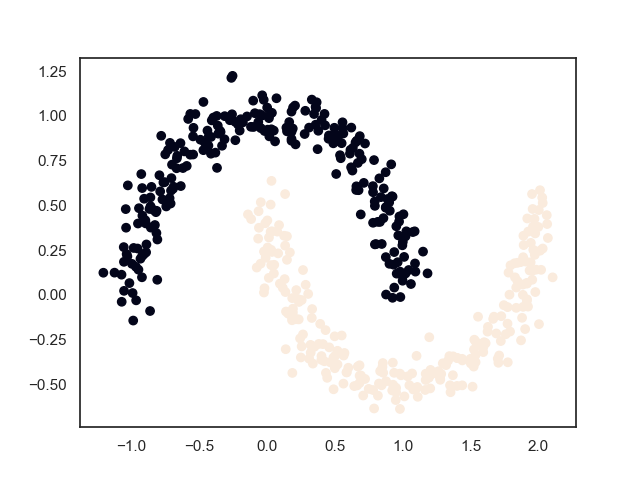
4. 学习算法
Init:
- 初始化样本空间中的每个样本作为一个簇,即初始化簇集 \(C_j=\{x_j|1\leq j \leq N\}\),样本标签 \(Y=\{j|1\leq j \leq N\}\)
- 初始化簇间距离矩阵 \(M=[m_{ij}]_{N \times N}\),其中,\(m_{ij}=\infty\)(距离为无穷大表示 \(x_i\) 与 \(x_j\) 之间的距离可以被忽略)
- 重新赋值计算距离矩阵 \(m_{ij} = d(C_i,C_j)=||x_i-x_j||^2,i<j\)(西瓜书上将整个矩阵都重新计算了,但由于距离矩阵是一个关于 \(i=j\) 对称的矩阵,所以只需要更新 \(i<j\) 区域的值即可)
Repeat:
- 寻找距离最近的两个类簇,即 \((i,j)=\arg \min_{1 \leq i \leq N, i<j\leq N} m_{ij}\)
- 寻找 \(x_i\) 和 \(x_j\) 对应的簇 \(C_I\) 和 \(C_J\),即 \(C_I=\{x \in X|y=y_i\},C_J=\{x \in X|y=y_j \}\)
- 合并 \(C_I\) 与 \(C_J\),即簇集更新为 \(C_I=C_I \cup C_J\),\(C_J\) 簇的标签更新为 \(C_I\) 簇的标签,即 \(Y_J = \{y=y_i|x \in C_J \}\)
- 将同一个簇的簇间距离更新为无穷大,即 \(\{m_{ij} = \infty | x_i \in C_I, x_j \in C_J\}\),因为这里只需要更新半个距离矩阵,所以需要重新调整更新下标 \((i,j)=(\min(i,j),\max(i,j))\)
Until: 簇集 \(C\) 的集合数量为 \(k\)
End: 对输出标签重新排序编号为 \(\{0,1,...,k\}\)
5. references
《统计学习方法》14.2节,李航
《机器学习》9.6节,周志华
Good luck~