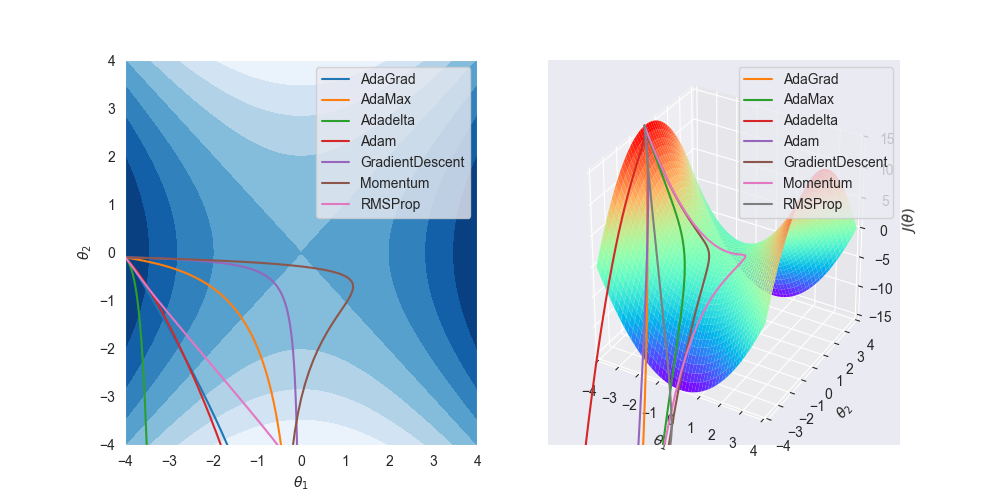
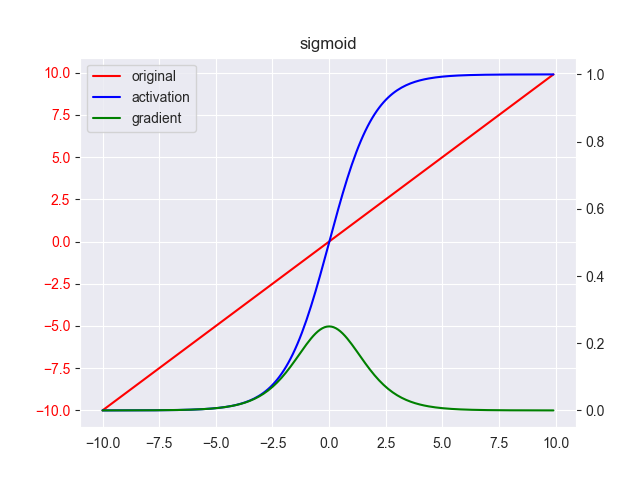
基于numpy的实现代码传送门
1. 基本定义
损失函数(loss function),指单个样本的误差,即 \(L(y_i,f(x_i);\theta)\),\(y_i\) 为真实值,\(f(x_i)\) 为预测值
代价函数(cost function)(也有说法称其可以等价为风险函数(risk function)),指模型的总体误差,一般取平均误差,即 \(J(\theta)=\frac{1}{N} \sum_i^N L_i(y, f(x);\theta) = \frac{1}{N} 1^T \cdot L(y, f(x);\theta)\),对应的偏导为 $ = _i $
目标函数(Objective Function),指模型最终的优化函数,一般是最小化代价函数加上正则化项,即 \(\theta = \arg \min _\theta (J(\theta)+\lambda \Phi(\theta))\)
注:
但也有说法认为损失函数与代价函数是等价,莫衷一是,虽然叫法不一,但总体做法是一样的,只是中间的每个流程步骤叫法不一而已,不用太过纠结。本文倾向于前者的定义。
损失函数一般可以分为分类损失或回归损失,而分类损失又可以继续分为二分类型或多分类型损失。
2. 变量定义
下面的公式中,为了表示方便,定义
- \(y,f(x)\) 均为 \(n\) 维列向量
- 诸如 \(yf(x)\) 形式的运算,如无特殊说明,默认为哈达玛积,即对应位相乘,返回仍为一个 \(n\) 维列向量
- 诸如 \(y^Tf(x)\) 形式的运算,如无特殊说明,默认为矩阵乘法
3. 回归损失
先来一张全家福
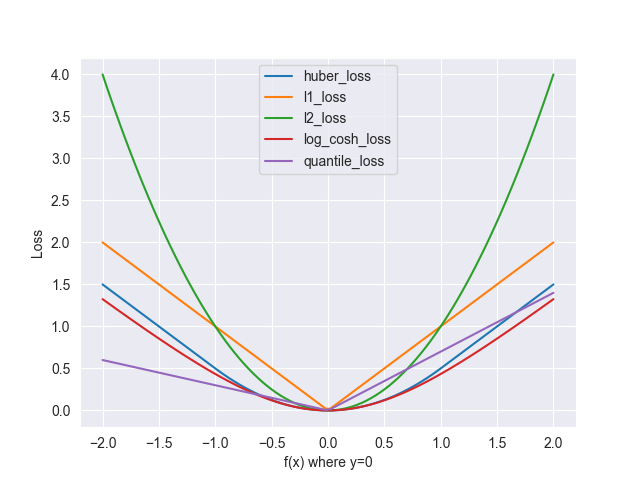
3.1. L1 loss
又称绝对值损失函数,多用于回归问题,其表达式为 \[ L(y,f(x)) = |y-f(x)| \]
对应的偏导为 \[ \frac{\partial L }{\partial f } = \left\{\begin{array}{l}1 &, f(x) > y \\ -1 &, f(x) \leq y \end{array}\right. \]
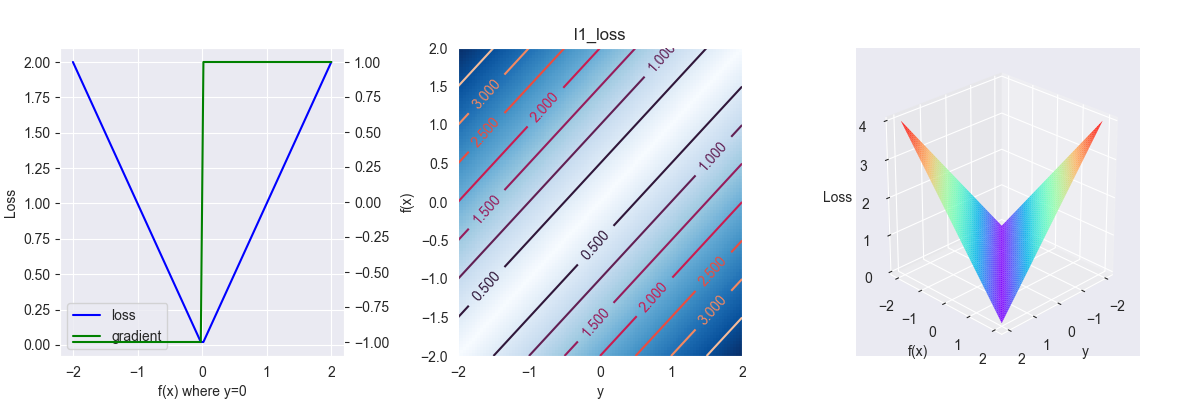
图像说明,下同。
上图中,第一张图为 \(y=0\) 时,\(L\) 关于 \(f(x)\) 的函数(对应左侧坐标系)及其偏导(对应右侧坐标系)曲线图;第二张图为 \(L\) 关于 \(y-f(x)\) 超平面的剖面和等高线图,其中,颜色越深表示高度越高,反之则越低,梯度下降即从高走到低,颜色变化程度表示梯度的大小,梯度越大,下降越快,反之则越慢;第三张为立体3d图,可以很清晰看出其梯度变化情况。
特别的,我们还可以从函数图中得出一些初步的结论:
- 函数图越接近线性,权重更新越不受异常点干扰,模型的鲁棒性(这不忍直视的翻译,robust的音译,意为健壮性)越好
- 函数一般是凸函数,其中每个峰谷(对应偏导的零点处)都是一个局部最优解
- 函数图像每个点的斜率的绝对值越大,坡度越大,下降的速度越快,拟合所需的时间越短
优点
- 绝对值损失一个很大的特点是其函数图像是线性的,这意味梯度下降并不受异常点干扰,系统的鲁棒性很好。
缺点
- 导数不连续,因此求解效率较低
- 梯度是一个常量,这对与训练来说是不利的,因为到了训练后期,loss值往往会变得很小,如果还以很大的梯度进行下降,很容易找到不到最优解,在最优解附近来回震荡,如果下降步长没有做自适应处理,甚至会不收敛。
3.2. L2 loss
又称平方损失函数,多用于回归问题,其表达式为 \[ L(y , f(x))=(y-f(x))^{2} \]
对应的偏导为 \[ \frac{\partial L }{\partial f } = f(x) - y \]
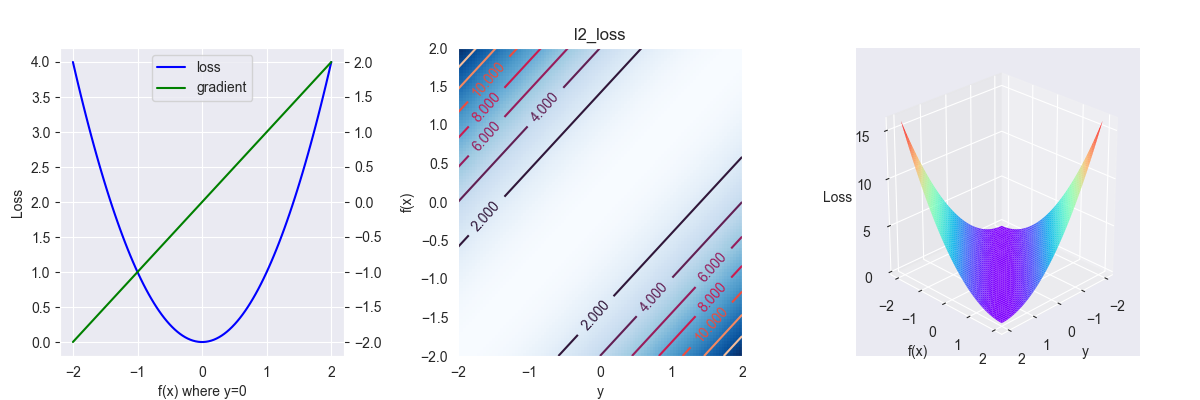
下降速度先快后慢,很适合模型训练,但模型受异常点的影响很大,而且会偏向于向异常点进行偏移
3.3. Huber loss
平滑平均绝对损失函数,其表达式为 \[ L_{\delta}(y, f(x))=\left\{\begin{array}{ll}\frac{1}{2}(y-f(x))^{2} &, |y-f(x)| \leq \delta \\ \delta|y-f(x)|-\frac{1}{2} \delta^{2} &, |y-f(x)| > \delta\end{array}\right. \] 其中,\(\delta \in [0,+\infty]\)
对应的偏导为 \[ \frac{\partial L }{\partial f } = \left\{\begin{array}{l}\frac{1}{2}(f(x)-y) &, |y-f(x)| \leq \delta \\ -\delta &, y-f(x)>\delta \\ \delta &, y-f(x) < -\delta\end{array}\right. \]
下面是 \(\delta=1\) 时图像
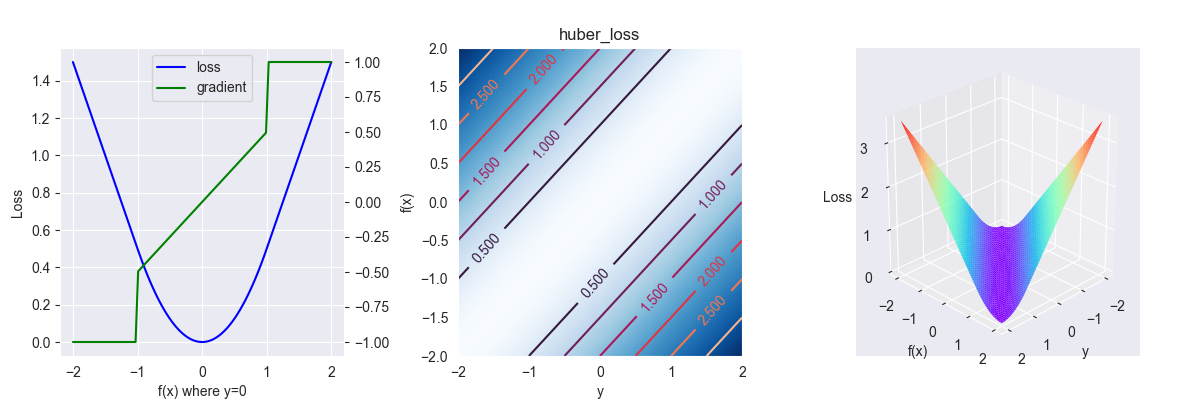
这是对 \(L_1\) 和 \(L_2\) 损失的权衡,\(\delta\) 趋向于0时,退化为 \(L_1\) 损失;\(\delta\) 趋向于正无穷时,退化为 \(L_2\) 损失。
该函数的特点是,训练初期,以一个较大的梯度均匀下降,到了训练后期,坡度逐渐放缓。
3.4. Log-Cosh loss
对数双曲余弦损失函数,其表达式为 \[ L\left(y, f(x)\right)= \ln \left(\cosh \left(f(x)-y\right)\right) \] 对应的偏导为 \[ \frac{\partial L }{\partial f } = -\tanh(f(x)-y) \]
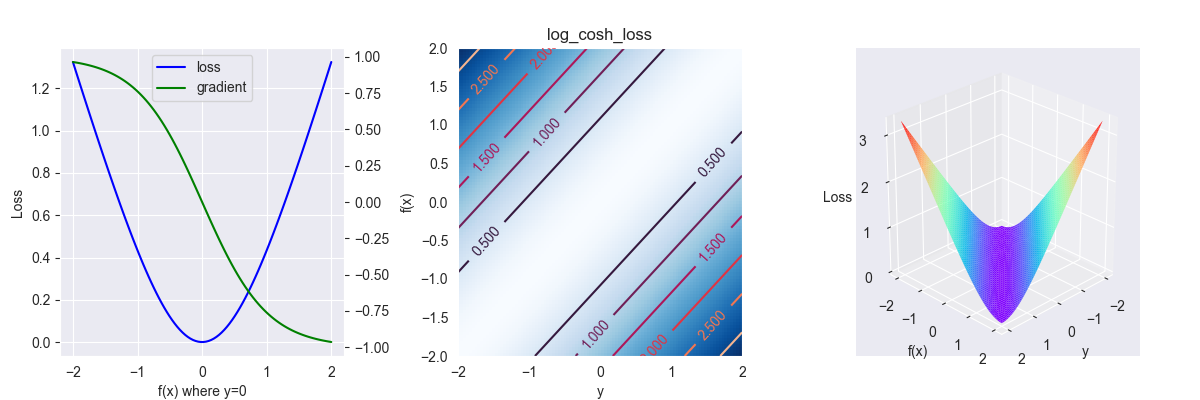
对于较小的\(x\),\(\log(\cosh(x))\)近似等于\((x^2)/2\);对于较大的\(x\),近似等于\(|x|-\ln2\)
该函数是对\(L_2\) 的改进,其函数图像更为平滑,也可以看做Huber loss的替代品,其优点是连续的且处处可微。
3.5. Quantile loss
分位数损失函数,其表达式为 \[ L(y, f(x))=\left\{\begin{array}{l}(1-\gamma)|y-f(x)| &, y < f(x) \\ \gamma|y-f(x)| &, y \geq f(x)\end{array}\right. \] 其中,\(\gamma \in [0,1]\)
对应的偏导为 \[ \frac{\partial L }{\partial f } = \left\{\begin{array}{l}1-\gamma &, y < f(x) \\ \gamma &, y \geq f(x) \end{array}\right. \]
下面是 \(\gamma=0.3\) 时的图像
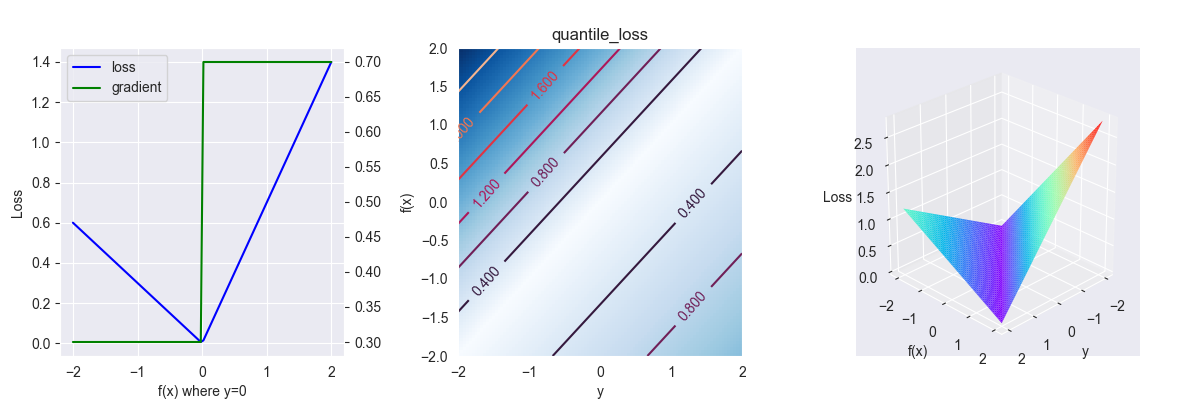
这是一个带偏向性的损失函数,\(\gamma\) 值越大,模型在预测值比真实值小的数据中的拟合速度越快。
4. 分类损失
先来一张全家福
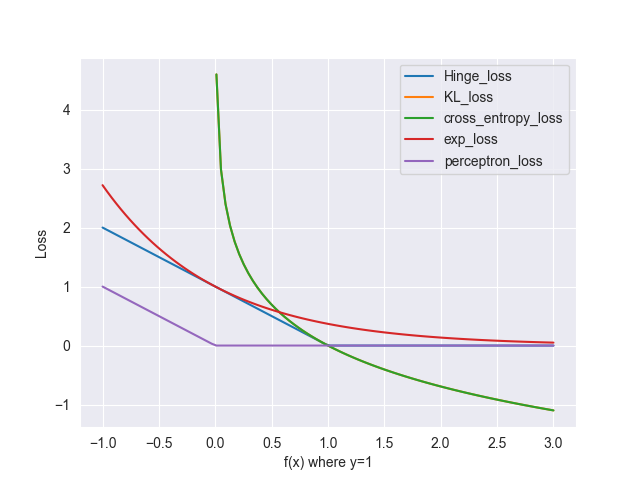
由于y=1,KL散度与交叉熵的曲线重合在一起了
分类损失与回归损失最大的不同是其下降的方向是单向的,
4.1. zero-one loss
0-1损失函数,二分类的表达式 \[ L(y, f(x))=\left\{\begin{array}{l}1, f(x) > \delta \\ 0, f(x) \leq \delta \end{array}\right. \] 其中,\(\delta\) 为分类阈值,一般取二分类的中点
扩展至多分类的表达式 \[ L(y, f(x))=\left\{\begin{array}{l}1, y \neq f(x) \\ 0, y=f(x)\end{array}\right. \]
对应的偏导为 \[ \frac{\partial L }{\partial f } = 0 \] 0-1损失函数直接对应分类判断错误的个数,但是它是一个偏导恒为0的非凸函数,无法使用类似梯度下降的方法求解,使用的场合很少。
典型使用者:感知机模型
4.2. Cross entropy loss
交叉熵损失函数,多用于概率型模型,二分类的表达式 \[ L(y, f(x))=\left\{\begin{array}{l}-y\ln f(x) &, y=1 \\ -(1-y)\ln (1-f(x)) &, y=0 \end{array}\right. \] 其中,\(y\in\{0,1\},f(x)\in[0,1]\),\(f(x)\) 多为概率分布函数。
特别地,最小化交叉熵函数与最大化似然函数是等价的。
扩展至多分类的表达式 \[ L(y,f(x)) = -y \ln f(x) \]
其中,\(y\in \mathbb R^{n},y_i \in \{0, 1\}, f(x)\in \mathbb R^{n},f(x_i)\in[0,1]\)
对应的偏导为 \[ \frac{\partial L }{\partial f } = -\frac{y}{f(x)} \]
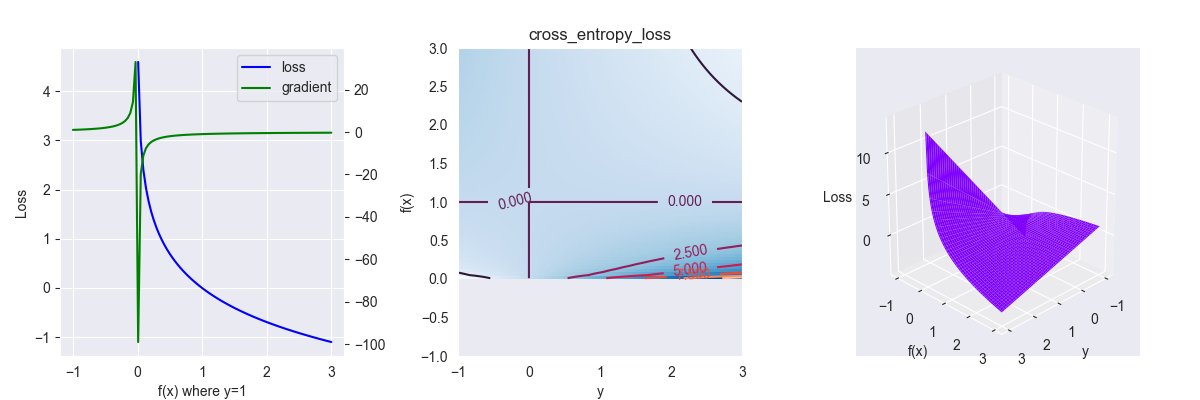
由于批量作图时没有限制定义域,上面第一张图和第二张图中存在错误:在 \(f(x) \leq 0\) 和 \(y<0\) 的部分也存在函数图像
其函数图像非线性程度很大,对异常点非常敏感
误差大的时候,权重更新快;误差小的时候,权重更新慢
典型使用者:逻辑回归
特别地,交叉熵一般会与softmax一起使用,组合成softmax cross entropy loss,下面给出其表达形式 \[ L(y_i,x_i) = -y_i \ln \frac{e^{x_i} }{\sum_j e^{x_j}} \] 由于上一篇笔记数学工具-激活函数中已经算出softmax的导数形式为 \[ \frac{\partial f_i }{\partial x_j } = \left\{\begin{array}{l}f_i(1-f_i) &, i=j \\ -f_i f_j &, i \neq j\end{array}\right. \] 其中,\(i\) 为当前预测的样本,\(j\) 为目标输出样本,则其偏导为 \[ \frac{\partial L_i }{\partial x_i } = \frac{\partial L_i }{\partial f_i } \cdot \frac{\partial f_i }{\partial x_i } =\left\{\begin{array}{l}f_j-1 &, i=j \\ f_j &, i \neq j\end{array}\right. \] 其偏导形式极其简单,只取决于最高的预测值,故其反向迭代计算代价很低。
4.3. KL散度
Kullback-Leibler散度(Kullback-Leibler divergence),又称相对熵(relative entropy),其表达式为 \[ L(y,f(x)) = y \ln \frac{y}{f(x)} \] 其中,\(y\in\{0,1,...\},f(x)\in[0,1]\),\(f(x)\) 多为概率分布函数。
对应的偏导为 \[ \frac{\partial L }{\partial f } = - \frac{y}{f(x)} \]
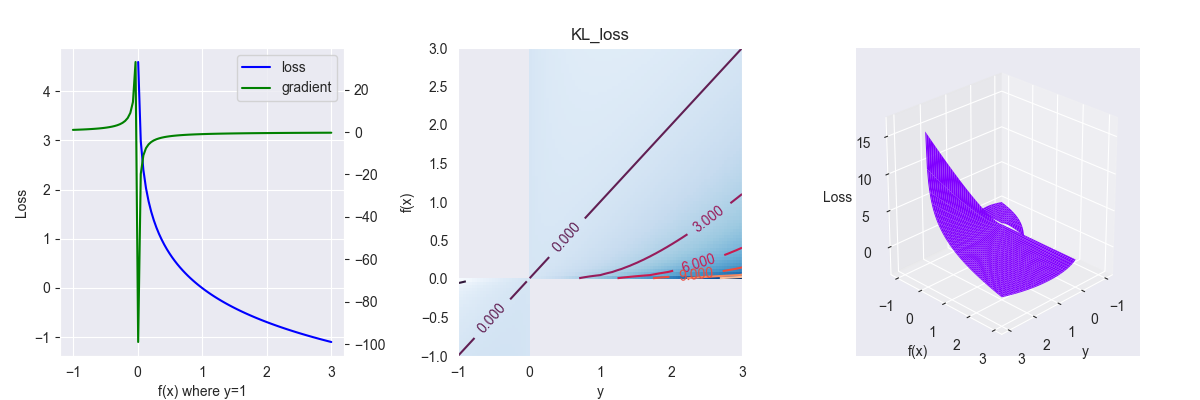
由于批量作图时没有限制定义域,上面第一张图和第二张图中存在错误,在 \(f(x) \leq 0\) 和 \(y<0\) 的部分不应该存在函数图像
KL散度表示两个概率分布间的非对称度量或距离,其跟交叉熵关系为:$L_{KL} = L_{cross} + yy $,由于KL散度多了一个不可优化的常数项,而常数项梯度下降时会被忽略,两者优化的时候是等价的,故一般使用交叉熵而不使用相对熵。特别地,当 \(y=1\) 时,定义域范围内,两者完全等价
4.4. exponential loss
指数损失函数,其表达式为 \[ L(y , f(x))=\exp (-y f(x)) \]
对应的偏导为 \[ \frac{\partial L }{\partial f } = -f(x)\exp (-y f(x)) \]
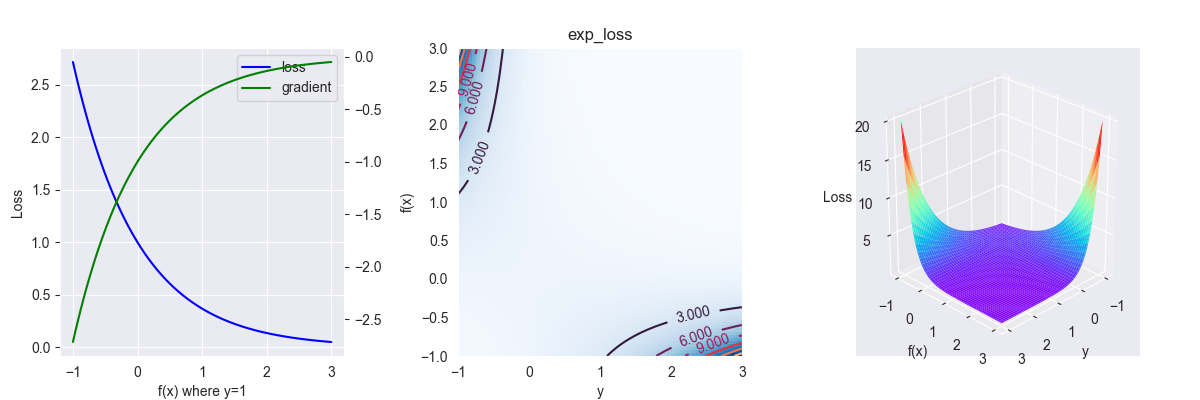
函数图像的非线性程度仅次于交叉熵,对异常点特别敏感
典型使用者:AdaBoost
4.5. Hinge loss
合页函数(因其函数表达式像合并的书页而得名),多用于二分类问题,其表达式为 \[ L(y, f(x))=\max (0,1-y f(x)) \]
其中,\(y\in\{-1,1\}\)
对应的偏导为 \[ \frac{\partial L }{\partial f } = \left\{\begin{array}{l}0 &, yf(x) > 1 \\ -f(x) &, yf(x) \leq 1\end{array}\right. \]
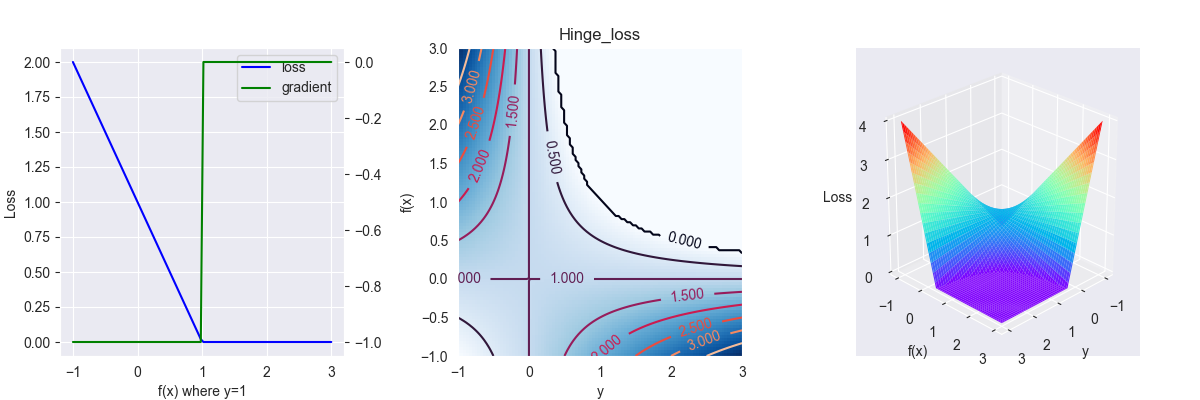
合页函数不鼓励分类器过度自信,让某个正确分类的样本距离分割线超过1并不会有任何奖励,从而使分类器可以更专注于整体的误差
经典使用者:SVM
4.6. perceptron loss
感知损失函数,多用于二分类问题,其表达式为 \[ L(y, f(x))=\max (0,- f(x)) \] 其中,\(y\in\{-1,1\}\)
对应的偏导为 \[ \frac{\partial L }{\partial f } = \left\{\begin{array}{l}0 &, f(x) > 0 \\ -1 &, f(x) \leq 0\end{array}\right. \]
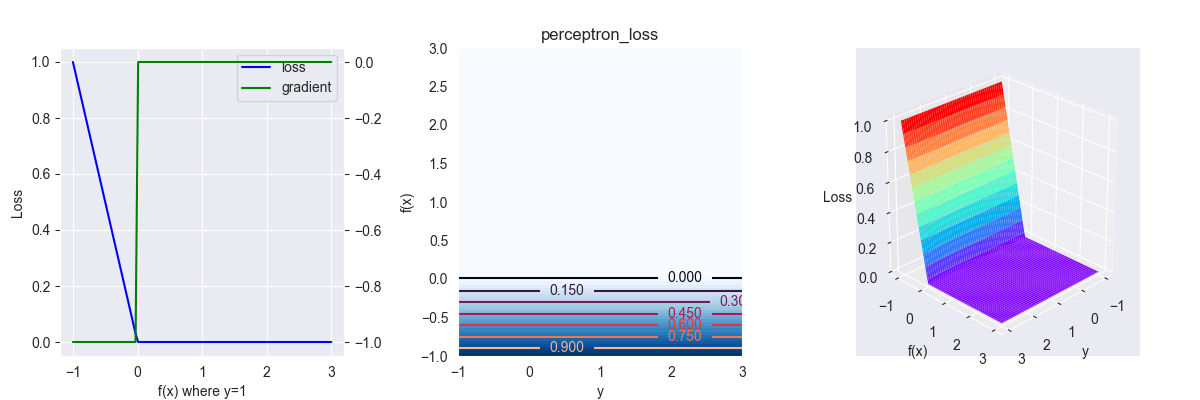
感知损失函数式是Hinge loss的变体,但其损失函数只取决于预测值,与真实值没有任何关系,对其数学理论支撑表示怀疑。
5. references
https://www.jiqizhixin.com/articles/2018-06-21-3
Keep up~