实现代码传送门
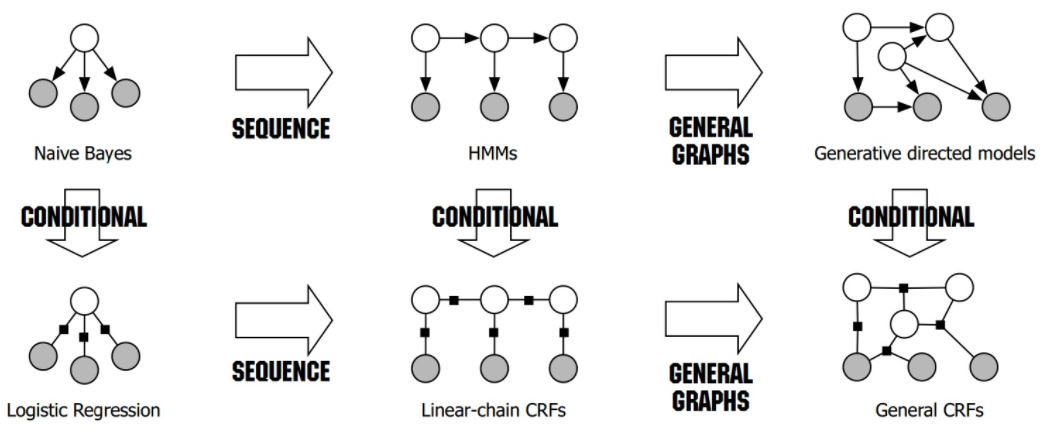
HMM的相关原理参考我的上一篇笔记:标注算法-HMM
下面以中文分词demo作为例子,介绍HMM在分词我任务中的应用。
1. 预处理
1.1. 训练集选择
推荐采用人民日报的词性标注语料集。
目前有2014版和1998版,前者语料库规模比后者的大,后者为人工标注版本,前者精度上相比要差一些,但前者的语料较为鲜活,与当前主流的中文书写习惯更为接近。
这里采用2014版语料集,该语料的其中一行如下:
人民网/nz 1月1日/t 讯/ng 据/p 《/w [纽约/nsf 时报/n]/nz 》/w 报道/v ,/w 美国/nsf 华尔街/nsf 股市/n 在/p 2013年/t 的/ude1 最后/f 一天/mq 继续/v 上涨/vn ,/w 和/cc [全球/n 股市/n]/nz 一样/uyy ,/w 都/d 以/p [最高/a 纪录/n]/nz 或/c 接近/v [最高/a 纪录/n]/nz 结束/v 本/rz 年/qt 的/ude1 交易/vn 。/w 原始语料包含了词性标注,由于这里只用于分词任务,故需要先将其词性标签去除。
在处理的时候,有一个点需要特别注意,该语料集有两种细粒度可供选择,如 [纽约/nsf 时报/n]/nz,这表示既可以切分为 纽约时报 一个单词,也可以切分为 纽约 和 时报 两个单词。
本文采用了细粒度更小的后者。
1.2. 标注方式
中文分词字标注通常有2-tag、4-tag和6-tag这几种方法,其中,又以4-tag标注最为常用
2-tag
标注集合为{B,I},其将词首标记设计为B,而将词的其他位置标记设计为I。
中/B 华/I 人/B 民/I 共/B 和/I 国/I即标记“切分/不切分”就够了,优点是模型简单,训练速度较快;缺点是对语义规律的总结是片面的,导致模型的准确率较低
4-tag
标注集合为{S,B,M,E},S表示单字为词,B表示词的首字,M表示词的中间字,E表示词的结尾字。
中/B 华/M 人/B 民/M 共/B 和/M 国/E优点是一定程度上总结语义规律,兼顾了2-tag和6-tag的特点,即使是使用分词效果一般的HMM模型,也可以得到不错的效果。
6-tag
标注集合为{S,B,M1,M2,M,E},S表示单字为词,B表示词的首字,M1/M2/M表示词的中间字,E表示词的结尾字。
中/B 华/M1 人/M2 民/M 共/M 和/M 国/E优点是进一步总结了语义规律,更加易于发现长词;缺点是其对更多的字的位置进行了固定,需要大量的训练集支撑训练结果。
本文采用4-tag标注方式
1.3. 文本存储格式
常用的存储格式为
char1<break1>tag1<break2>char2<break1>tag2<break2>...其中,break<n> 为第n级分割符,特别地,break1 是1级分割符,表示单词和标记符号间的分割;break2 是2级分割符,表示单词间的分割;break3 是3级分割符,表示段落间的分割,以此列推。
常用如下两套分割方案
break1='/', break2=' ', break3='\n', break4='\n\n', ...(每增加一个大纲级别,增加一个回车符,以此列推),例如祝/S 伟/B 大/E 祖/B 国/E 繁/B 荣/M 昌/M 盛/E !/S 祝/S 全/B 区/E 各/B 族/E 人/B 民/E 在/S 新/B 的/E 一/B 年/E 里/S 幸/B 福/E 安/B 康/E 、/S 扎/B 西/E 德/B 勒/E !/Sbreak1='\t', break2='\n', break3='\n\n', break4='\n\n\n', ...(每增加一个大纲级别,增加一个回车符,以此列推),例如祝 S 伟 B 大 E 祖 B 国 E 繁 B 荣 M 昌 M 盛 E ! S
本文采用第二种存储格式
2. 模型设计
一些参数的具体取值如下:
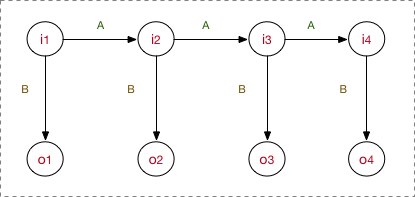
Q={'B', 'M', 'E', 'S'}, V={所有字符的集合}O和I表示每次输入的序列,例如,O='祝伟大祖国繁荣昌盛!', I='SBEBEBMMES'N=len(Q), M=len(V), S=len(seq)
2.1. 未知参数学习
因为是有监督学习,所以直接按照公式求解三元组 \((A,B,\pi)\) 即可
特别地,在后面结果预测的步骤中有乘法操作,为了防止向下溢出,下面展示的最终结果都经过了 \(\log\) 对数处理,其中 \(\log 0\) 取 \(-1e^{-9}\) 代替无穷小。
2.1.1. 初始状态\(\pi\)
\[ \pi_k = \log \frac{\sum_S(i_1=q_k)}{S} \]
训练结果
B -0.35712716996161437
M -1000000000.0
E -1000000000.0
S -1.20291840490418232.1.2. 转移概率矩阵 \(A\)
\[ a_{i j}=\log \frac{A_{i j}}{\sum_{j=1}^{N} A_{i j}} \]
训练结果
B M E S
B -1000000000.0 -1000000000.0 -0.684810767901495 -0.7551392365415603
M -0.3996402748676947 -1.1103647401125116 -1000000000.0 -1000000000.0
E -0.16180464296111247 -1.9011772741974273 -1000000000.0 -1000000000.0
S -1000000000.0 -1000000000.0 -0.5258124050930225 -0.92759081040002事实上,实际训练中可能只能提供只有词频的训练集,一部分转移概率会无法计算。这里提供一个大概的估计方案(具体出处忘了 -_-||) \[ a_{(s|s)}=a_{(s|e)} = \pi_s\\a_{(b|s)} = a_{(b|e)} = \pi_b \] 另外,苏神在 字标注法与HMM模型 一文中给出了一个经验取值,这里也可以参考一下 \[ a_{(s|s)}=a_{(s|e)} = 0.3 \\a_{(b|s)} = a_{(b|e)} = 0.7 \]
2.1.3. 观测概率矩阵 \(B\)
\[ b_{j}(k)=\log \frac{B_{j k}}{\sum_{k=1}^{M} B_{j k}} \]
训练结果
B M E S
1 -4.518497982335498 -3.0320559244452023 -6.657433764192848 -6.537725478359201
纽 -8.661834062535963 -10.266377393929087 -10.24185808976377 -11.342070025548505
时 -5.649817195217472 -5.929086653096597 -5.321189787834555 -5.718670228629817
报 -5.890738992552965 -6.927055415985019 -6.088823142305065 -8.059478386294197
...2.2. 结果预测
采用维特比算法对结果进行预测
由于前面参数都已经取 \(\log\) 对数,所以下面相应的步骤也由乘法操作改为加法操作;原流程是递归的,下面改为循环,结果等价
流程伪代码如下:
Input:
单词序列 \(O = \{o_1,...,o_T\}\)
所有的可能状态序列 \(Q=\{q_1,...,q_N\}\)
三元组 \((A,B,\pi)\)
Init:
\(\text{for} \quad i \quad \text{in} \quad \{1,...,N\}\)
\(\delta_1 = \pi_i + b_i(o_1)\)
\(\Psi_1(i)= \{i\}\)
Loop:
\(\text{for} \quad t \quad \text{in} \quad \{2,...,T\}\)
- \(\text{for} \quad i \quad \text{in} \quad \{1,...,N\}\)
- \(\delta_t(i) = \max_{1\leq j \leq N} [\delta_{t-1}(j) + a_{ji}] + b_i(o_t)\)
- \(\Psi_t(i) =\Psi_{t-1}(i)+ \{\arg \max_{1\leq j \leq N} [\delta_{t-1}(j) + a_{ji}] \}\)
Output:
预测状态序列 \(I=\Psi_T(\arg \max_{1 \leq i \leq N} \delta_T(i))\)
3. 分词效果展示
['结婚', '和', '尚未', '结婚', '的', '人']
['隐马尔', '可夫', '模型', '中有', '两个', '序列', ',', '一个', '是', '状态', '序列', ',', '另一个', '是', '观测', '序列', ',', '其中', '状态', '序列', '是', '隐藏', '的', '。']可以看出,基于HMM的分词,基本满足简单的分词需求,但其分词效果并不是很完美,可以看出 隐马尔可夫 这个新词并未被分出来,中有 这个词明显分词错误。
4. references
《统计学习方法》第10章,李航