机器学习标注算法

机器学习

发布日期: 2021-01-28

更新日期: 2022-08-10

文章字数: 3.3k

阅读时长: 15 分

阅读次数:

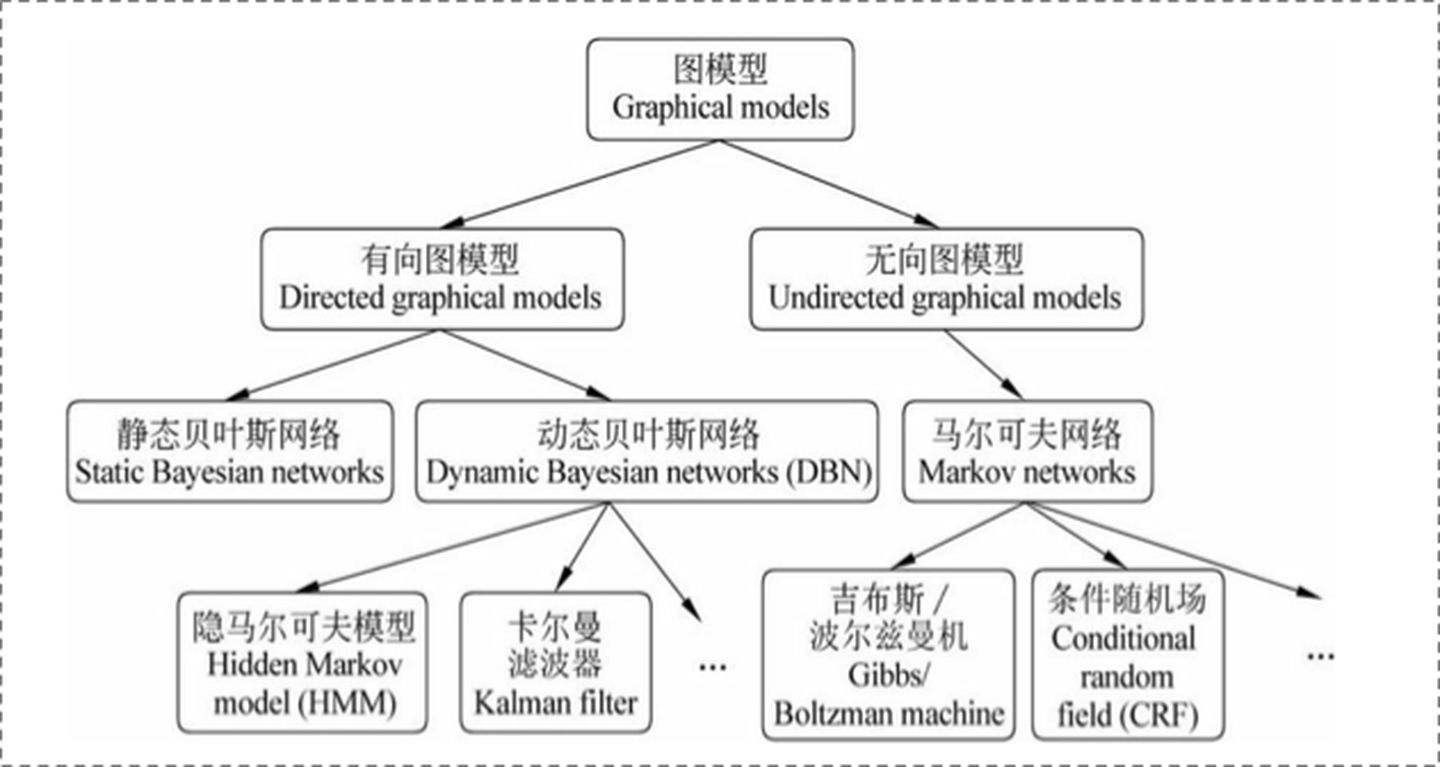
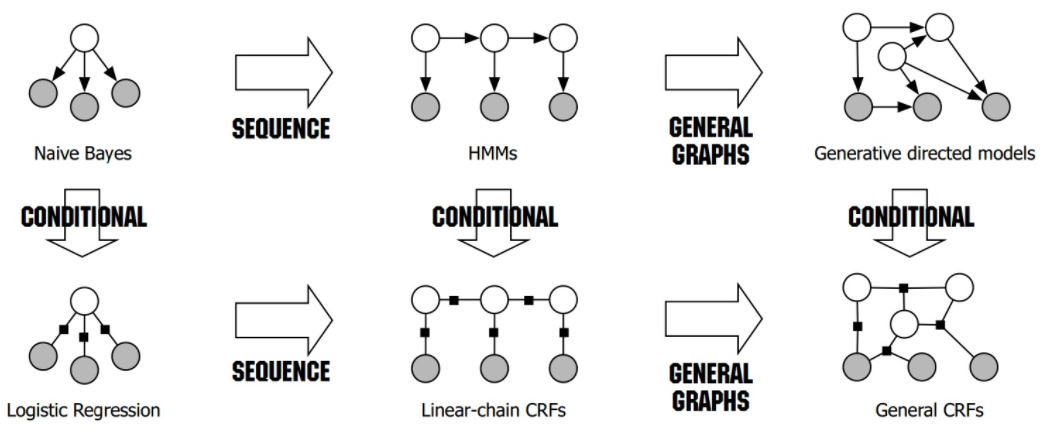
条件随机场（conditional random field，CRF）是一种基于概率无向图的时序标注算法

上面这种说法并不严谨，一般的CRF并不只用于标注问题，而用于标注问题的一般也被称为线性CRF（linear-CRF）

1. CRF与HMM的区别

1.1. 判别式与生成式

两者最大的区别是，CRF属于判别式模型，HMM属于生成式模型。

简单来说

判别式模型是对 \(P(Y|X)\) 的建模，即根据输入 \(X\) 直接给出 \(Y\) 出现的概率，只要确认一个划分边界，即可进行分类。其优点是对数据量要求没生成式的严格，速度也会快，小数据量下准确率也会好些。例如，绝大多数的神经网络、SVM等都属于判别式模型
生成式模型是对 \(P(X,Y)\) 的建模，其包含了所有可能的 \(X\) 以及所有可能的 \(Y\)，一般用于回归，如果要用于分类，则需要使用条件概率计算 \(P(Y|X)=\frac{P(X,Y)}{P(X)}\)。其优点是所包含的信息非常齐全，例如，线性回归、贝叶斯网络等都属于生成式模型

1.2. 有向图与无向图

两者的关系可以表示如下

更加具体的可以表示为

对于有向图，其联合概率一般表示为累乘的结果，累乘的过程根据图的结果而定，例如下图的联合概率表示为

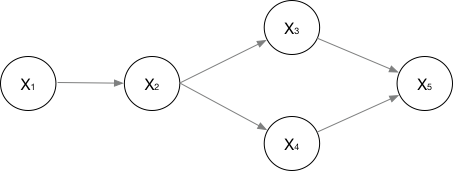
Di_graph \[ P(x_1,...,x_n) = P(x_1) \cdot P(x_2 \mid x_1) \cdots P(x_3 \mid x_2) \cdot P(x_4 \mid x_2) \cdot P(x_5 \mid x_3, x_4) \] 对于无向图，按照 Hammersley-Clifford 定理，其联合概率分布可以表示为 \[ P(Y) = \frac{1}{Z} \prod_C \psi_C(Y_C) \] 其中，\(C\) 是图的最大团， \(\psi_C(X_C) = \exp(-E(X_C))\) 被称为势函数，\(Z=\sum_X\prod_C \psi_C(X_C)\) 被称为规范化因子，这一项也是无向图模型中最难计算的一项，这一项含义是计算出所有可能的 \(x\) 对应的势函数，再对所有可能的输出求和。

下图的联合概率可以表示为

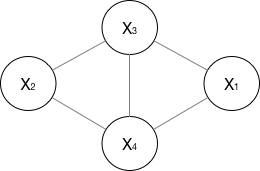
Udi_graph \[ P(X) = \frac{1}{Z(x)} (\psi_1(X_1,X_3,X_4)\cdot \psi_2(X_2,X_3,X_4)) \]

\[ Z(x) = \psi_1(X_1,X_3,X_4)\cdot \psi_2(X_2,X_3,X_4) + \psi_1(X_1,X_3,X_2)\cdot \psi_2(X_1,X_4,X_2) + ... \]

可以看出无向图的最大团的计算量很大，对于CRF来说，如果一个 \(x\) 大小为\(n\)，每个 \(x\) 对应 \(m\) 个可能的标签 \(y\) ，时间复杂度为 \(O(n^{m})\) ，所以一般数据量太大的数据集，CRF就不太适用了

2. 输入输出

Input:

观测序列 \[ X=(x_1,...,x_n) \] Output:

状态序列 \[ Y=(y_1,...y_n) \]

3. 模型推导

3.1. 基本定义

CRF师承最大熵模型，故其目标函数与学习方法与最大熵模型都较为相近。两者的差异在于特征函数的构造不一样。

同时，CRF也是从隐马尔科夫中引申出来的，其在HMM的基础上加上概率图模型和团的思想，把可观测符号的独立性假设去掉了。

CRF和最大熵模型一样，其关键是特征函数的构建。

对于给定的序列 \(X\) 和 \(Y\)，CRF模型可以用一个四元组 \((t_k,\lambda_k,s_l,u_l)\) 表示。

其中， \(t_k=t_{k}\left(y_{i-1}, y_{i}, x, i\right)\) 和 \(s_l = s_{l}\left(y_{i}, x, i\right)\) 分别是转移特征和状态特征函数，函数表达式一般是只要满足输入条件返回1否则返回0（实际上，可以直接将特征函数看做是一个规则的集合，而CRF就是学习这些规则的输出权重，某种意义下，可以将学好的CRF看做是决策树），\(\lambda_k\) 和 \(u_l\) 是对应的权值，\(k\) 为无向图中边的数量，\(l\) 为无向图中点的数量。

特别地，上面函数式中输入为小写的 \(x\) ，表示序列中的某个取值，如果按照函数的定义，应采用大写的 \(X\) 表示更加贴切

3.1.1. 参数化形式

\[ P(y \mid x)=\frac{1}{Z(x)} \exp \left(\sum_{i, k} \lambda_{k} t_{k}\left(y_{i-1}, y_{i}, x, i\right)+\sum_{i, l} \mu_{l} s_{l}\left(y_{i}, x, i\right)\right) \]

其中，\(Z(x)\) 是规范化因子 \[ Z(x)=\sum_{y} \exp \left(\sum_{i, k} \lambda_{k} t_{k}\left(y_{i-1}, y_{i}, x, i\right)+\sum_{i, l} \mu_{l} s_{l}\left(y_{i}, x, i\right)\right) \]

3.1.2. 简化形式

将 \(t_k\) 和 \(s_l\) 组成一个函数，记作 \[ f_{k}\left(y_{i-1}, y_{i}, x, i\right)=\left\{\begin{array}{l} t_{k}\left(y_{i-1}, y_{i}, x, i\right), \quad k=1,2, \cdots, K_{1} \\s_{l}\left(y_{i}, x, i\right), \quad k=K_{1}+l ; l=1,2, \cdots, K_{2} \end{array}\right. \]

对转移和状态特征在各个位置 \(i\) 求和

\[ f_{k}(y, x)=\sum_{i=1}^{n} f_{k}\left(y_{i-1}, y_{i}, x, i\right), \quad k=1,2, \cdots, K \]

\(w_k\) 表示特征 \(f_{k}(y, x)\) 的权值 \[ w_{k}=\left\{\begin{array}{ll} \lambda_{k}, & k=1,2, \cdots, K_{1} \\ \mu_{l}, & k=K_{1}+l ; l=1,2, \cdots, K_{2} \end{array}\right. \]

将两者分别以其向量形式表示 \[ w=\left(w_{1}, w_{2}, \cdots, w_{K}\right)^{\mathrm{T}} \]

\[ F(y, x)=\left(f_{1}(y, x), f_{2}(y, x), \cdots, f_{K}(y, x)\right)^{\mathrm{T}} \] 目标函数为 \[ P_{\mathrm{w}}(y \mid x)=\frac{\exp (w \cdot F(y, x))}{Z_{\mathrm{w}}(x)} \] 其中 \[ Z_{\mathrm{w}}(x)=\sum_{y} \exp (w \cdot F(y, x)) \]

3.1.3. 矩阵形式

将简化形式进一步表达为矩阵形式

首先定义一个 \(m\) 阶矩阵随机变量

对于 \(x\) 的每一个位置 \(i=1,2,...,n+1\)，有 \[ M_{i}(x)=\left[m_{i}\left(y_{i-1}, y_{i} \mid x\right)\right] \]

其中， \[ m_{i}\left(y_{i-1}, y_{i} \mid x\right)=\exp \left(W_{i}\left(y_{i-1}, y_{i} \mid x\right)\right) \]

\[ W_{i}\left(y_{i-1}, y_{i} \mid x\right)=\sum_{i=1}^{K} w_{k} f_{k}\left(y_{i-1}, y_{i}, x, i\right) \]

目标函数为 \[ P_{\mathrm{w}}(y \mid x)=\frac{1}{Z_{\mathrm{w}}(x)} \prod_{i=1}^{n+1} M_{i}\left(y_{i-1}, y_{i} \mid x\right) \] 其中 \[ Z_{w}(x)=\left(M_{1}(x) M_{2}(x) \cdots M_{n+1}(x)\right)_{\text {start,stop }} \]

3.2. 概率计算问题

采用前向后向算法

首先定义前向向量 \[ \alpha_{0}(y \mid x)=\left\{\begin{array}{ll} 1, & y=\operatorname{start} \\ 0, & \text { otherwise } \end{array}\right. \] 有 \[ \alpha_{i}^{\mathrm{T}}\left(y_{i} \mid x\right)=\alpha_{i-1}^{\mathrm{T}}\left(y_{i-1} \mid x\right) M_{i}\left(y_{i-1}, y_{i} \mid x\right), \quad i=1,2, \cdots, n+1 \] 可以简单表示为 \[ \alpha_{i}^{\mathrm{T}}(x)=\alpha_{i-1}^{\mathrm{T}}(x) M_{i}(x) \] 然后定义后向向量 \[ \beta_{n+1}\left(y_{n+1} \mid x\right)=\left\{\begin{array}{ll} 1, & y_{n+1}=\text { stop } \\ 0, & \text { otherwise } \end{array}\right. \] 有 \[ \beta_{i}\left(y_{i} \mid x\right)=M_{i}\left(y_{i}, y_{i+1} \mid x\right) \beta_{i-1}\left(y_{i+1} \mid x\right) \] 可以简单表示为 \[ \beta_{i}(x)=M_{i+1}(x) \beta_{i+1}(x) \] 于是有

状态条件概率 \[ P\left(Y_{i}=y_{i} \mid x\right)=\frac{\alpha_{i}^{\mathrm{T}}\left(y_{i} \mid x\right) \beta_{i}\left(y_{i} \mid x\right)}{Z(x)} \]

转移条件概率 \[ P\left(Y_{i-1}=y_{i-1}, Y_{i}=y_{i} \mid x\right)=\frac{\alpha_{i-1}^{\mathrm{T}}\left(y_{i-1} \mid x\right) M_{i}\left(y_{i-1}, y_{i} \mid x\right) \beta_{i}\left(y_{i} \mid x\right)}{Z(x)} \] 其中 \[ Z(x)=\alpha_{n}^{\mathrm{T}}(x) \cdot \mathbf{1} = \mathbf{1} \cdot \beta_1(x) \] 概率图模型最难计算的归一化因子通过以上递推计算，最终计算变得非常简单，其实就是最后一个时刻的前向向量或第一个时刻的后向向量之和。

下面还有一些数学期望的计算 \[ \begin{aligned} E_{P(Y \mid X)}\left[f_{k}\right] &=\sum_{y} P(y \mid x) f_{k}(y, x) \\ &=\sum_{i=1}^{n+1} \sum_{y_{i-1} y_{i}} f_{k}\left(y_{i-1}, y_{i}, x, i\right) \frac{\alpha_{i-1}^{\mathrm{T}}\left(y_{i-1} \mid x\right) M_{i}\left(y_{i-1}, y_{i} \mid x\right) \beta_{i}\left(y_{i} \mid x\right)}{Z(x)} \end{aligned} \]

\[ \begin{aligned} E_{P(X,Y)}\left[f_{k}\right] &=\sum_{y} P(y \mid x) f_{k}(y, x) \\ &= \sum_x \tilde{P}(x)\sum_{i=1}^{n+1} \sum_{y_{i-1} y_{i}} f_{k}\left(y_{i-1}, y_{i}, x, i\right) \frac{\alpha_{i-1}^{\mathrm{T}}\left(y_{i-1} \mid x\right) M_{i}\left(y_{i-1}, y_{i} \mid x\right) \beta_{i}\left(y_{i} \mid x\right)}{Z(x)} \end{aligned} \]

3.3. 学习问题

学习算法可以采用改进的迭代尺度法或拟牛顿法，这两种方法在最大熵模型中也有被使用。

3.3.1. 改进的迭代尺度法

首先给出训练数据的对数似然函数 \[ \begin{aligned} L(w) &=L_{\tilde{P}}\left(P_{w}\right) \\ &=\log \prod_{x, y} P_{w}(y \mid x)^{\tilde{P}(x, y)} \\&=\sum_{x, y} \tilde{P}(x, y) \log P_{w}(y \mid x) \\&=\sum_{x, y}\left[\tilde{P}(x, y) \sum_{k=1}^{K} w_{k} f_{k}(y, x)-\tilde{P}(x, y) \log Z_{w}(x)\right] \\&=\sum_{j=1}^{N} \sum_{k=1}^{K} w_{k} f_{k}\left(y_{j}, x_{j}\right)-\sum_{j=1}^{N} \log Z_{w}\left(x_{j}\right) \end{aligned} \] 设

模型的当前参数向量 \(w = (w_1,...,w_K)^T\)；向量的增量为 \(\delta=(\delta_1,...,\delta_K)^T\)

则具体流程如下：

Input:

特征函数 \(t_1,...t_{K_1}\)，\(s_1,...,s_{K_2}\)；经验分布 \(P(x,y)\)
Init:

\(w_k=0,k\in\{1,..,K\}\)
Repeat:
1. 由方程 \[ \begin{aligned} E_{\tilde{p}}\left[t_{k}\right] &=\sum_{x, y} \tilde{P}(x, y) \sum_{i=1}^{n+1} t_{k}\left(y_{i-1}, y_{i}, x, i\right) \\ &=\sum_{x, y} \tilde{P}(x) P(y \mid x) \sum_{i=1}^{n+1} t_{k}\left(y_{i-1}, y_{i}, x, i\right) \exp \left(\delta_{k} T(x, y)\right) \end{aligned} \] 求解 \(\delta_k\)，其中，\(k \in \{ 1,2, \cdots, K_{1} \}\)
  
  上式 \(T(x,y)\) 表示数据 \((x,y)\) 出现所有特征出现的总数 \[ T(x, y)=\sum_{k} f_{k}(y, x)=\sum_{k=1}^{K} \sum_{i=1}^{n+1} f_{k}\left(y_{i-1}, y_{i}, x, i\right) \]
2. 由方程 \[ \begin{aligned} E_{\bar{P}}\left[s_{l}\right] & =\sum_{x, y} \tilde{P}(x, y) \sum_{i=1}^{n+1} s_{l}\left(y_{i}, x, i\right) \\ &=\sum_{x, y} \tilde{P}(x) P(y \mid x) \sum_{i=1}^{n} s_{l}\left(y_{i}, x, i\right) \exp \left(\delta_{K_{1}+l} T(x, y)\right) \end{aligned} \] 求解 \(\delta_{K_1+l}\)，其中，\(l \in \{1,2, \cdots, K_{2}\}\)
3. 更新 \(w_{k} \leftarrow w_{k}+\delta_{k}\)
Until:

所有的 \(w_k\) 都收敛
Output:

最优参数值 \(\hat w\)；最优模型 \(P_{\hat{w}}(y \mid x)\)

3.3.2. 拟牛顿法

省略求导过程给出

优化目标函数 \[ \min _{w \in \mathbf{R}^{n}} f(w)=\sum_{x} \tilde{P}(x) \log \sum_{y} \exp \left(\sum_{i=1}^{n} w_{i} f_{i}(x, y)\right)-\sum_{x, y} \tilde{P}(x, y) \sum_{i=1}^{n} w_{i} f_{i}(x, y) \]

梯度函数 \[ g(w) = \sum_{x,y}\tilde{P}(x)P_w(y\mid x)f(x,y)-E_\tilde{P}(f) \]

给出求解过程：

Input:

特征函数 \(f_1,...,f_n\)；经验分布 \(P(X,Y)\)
Init:

初始点 \(w^{(0)}\)；正定对称矩阵 \(B_0\)（例如n阶单位矩阵）
while \(g_{k}=g\left(w^{(k)}\right)=0\):
1. 由 \(B_{k} p_{k}=-g_{k}\) 求 \(p_k\)
2. 求 \(\lambda_k\) 使得 \[ f\left(w^{(k)}+\lambda_{k} p_{k}\right)=\min _{\lambda \geq 0} f\left(w^{(k)}+\lambda p_{k}\right) \]
3. 置 \(w^{(k+1)}=w^{(k)}+\lambda_{k} p_{k}\)
4. 求 \(B_{k+1}\) \[ B_{k+1}=B_{k}+\frac{y_{k} y_{k}^{\mathrm{T}}}{y_{k}^{\mathrm{T}} \delta_{k}}-\frac{B_{k} \delta_{k} \delta_{k}^{\mathrm{T}} B_{k}}{\delta_{k}^{\mathrm{T}} B_{k} \delta_{k}} \] 其中 \[ y_{k}=g_{k+1}-g_{k}, \quad \delta_{k}=w^{(k+1)}-w^{(k)} \]
Output:

最优参数值 \(\hat w\)；最优模型 \(P_{\hat{w}}(y \mid x)\)

3.4. 预测问题

采用维特比算法

初始化 \[ \delta_{1}(j)=w \cdot F_{1}\left(y_{0}=\text { start }, y_{1}=j, x\right), \quad j=1,2, \cdots, m \]
递推 \[ \delta_{i}(l)=\max _{1 \leqslant j \leqslant m}\left\{\delta_{i-1}(j)+w \cdot F_{i}\left(y_{i-1}=j, y_{i}=l, x\right)\right\} \]

\[ \Psi_{i}(l)=\arg \max _{1 \leqslant j \leqslant m}\left\{\delta_{i-1}(j)+w \cdot F_{i}\left(y_{i-1}=j, y_{i}=l, x\right)\right\} \]
终止 \[ \max _{y}(w \cdot F(y, x))=\max _{1 \leqslant j \leqslant m} \delta_{n}(j) \]

\[ y_{n}^{*}=\arg \max _{1 \leqslant j \leqslant m} \delta_{n}(j) \]
返回路径 \[ y_{i}=\Psi_{i+1}\left(y_{i+1}\right), \quad i=n-1, n-2, \cdots, 1 \]