1. 输入输出

Input:

观测序列 \[ O=(o_1,...,o_T) \] Output:

状态序列 \[ I=(i_1,...i_T) \]

2. 模型推导

2.1. 基本定义

过程或（系统）在时刻\(t_0\)所处的状态为已知的条件下，过程在时刻\(t>t_0\)所处状态的条件分布过程在时刻\(t_0\)之前所处的状态无关（即过程“将来”的情况与“过去”的情况是无关的。）的特性称为马尔科夫性或无后效性。

其中，时间和状态都是离散的马尔科夫过程称为马尔可夫链。

马尔可夫链描述了一种状态序列，其每个状态值取决于前面有限个状态。马尔可夫链是具有马尔可夫性质的随机变量的一个数列。这些变量的范围，即它们所有可能取值的集合，被称为“状态空间”。

当状态空间时不可观测时，则称其为隐马尔科夫

隐马尔科夫还对马尔科夫过程作出了延伸，提出了如下两个假设：

齐次马尔科夫性假设。又叫一阶马尔可夫假设，即任意时刻的状态只依赖前一时刻的状态，与其他时刻无关。即 \[ P\left(i_{t} \mid i_{t-1}, o_{t-1}, \cdots, i_{1}, o_{1}\right)=P\left(i_{t} \mid i_{t-1}\right) \]
观测独立性假设。任意时刻的观测只依赖于该时刻的状态，与其他状态无关。即 \[ P\left(o_{t} \mid i_{T}, o_{T}, \cdots, i_{t+1}, o_{t+1}, i_{t}, i_{t-1}, o_{t-1}, \cdots, i_{1}, o_{1}\right)=P\left(o_{t} \mid i_{t}\right) \]

HMM算法可以切分为3个独立的子问题：概率计算问题、学习问题、预测问题

为了便于说明，先给出如下各个符号的定义。

设

\(Q=\{q_1,...,q_N\}\) 是所有可能的状态的集合，\(V=\{v_1,...,v_M\}\) 是所有可能的观测的集合，其中，\(N\) 和 \(M\) 分别为可能观测到的状态数和观测数。
\(I=(i_1,...i_T)\) 是状态序列，\(O=(o_1,...,o_T)\) 为对应的观测序列。
\(A=[a_{ij}]_{N\times N}\) 是状态转移矩阵，其中，\(a_{ij}=P(i_{t+1}=q_j|i_t=q_i)\) 是 \(t\) 时刻状态 \(q_i\) 条件下在 \(t+1\) 时刻转移到 \(q_j\) 的概率
\(B=[b_j(k)]_{N \times M}\) 是观测概率矩阵，其中，\(b_j(k)=P(o_t=v_k|i_t=q_j)\) 表示 \(t\) 时刻处于 \(q_j\) 状态的条件下生成观测 \(v_k\) 的概率
\(\pi=(\pi_i)\) 是初始状态概率向量，其中，\(\pi_i=P(i_1=q_i)\) 表示 \(t=1\) 时刻处于 \(q_i\) 状态的概率

上述变量中，\(\pi,A,B\) 这三个变量决定了HMM模型的性能，这三个变量也称为HMM模型的三要素，故，HMM模型 \(\lambda\) 可以用三元组 \((A,B,\pi)\) 表示

上述变量的关系可简单如下表示

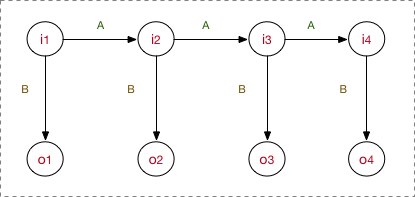
2.2. 概率计算问题

给定三元组 \((A,B,\pi)\) 以及观测序列 \(O\) ，计算在模型 \(\lambda\) 下 \(O\) 出现的概率 \(P(O|\lambda)\)

2.2.1. 直接计算法

基本思想为列举所有可能的状态序列 \(I\) ，求每个 \(I\) 与 \(O\) 的联合概率 \(P(O,I|\lambda)\)，然后对所有可能的状态序列求和，得到 \(P(O|\lambda)\)

具体计算流程如下：

状态序列 \(I\) 出现的概率 \[ P(I \mid \lambda)=\pi_{i_{1}} a_{i_{1} i_{2}} a_{i_{2} i_{3}} \cdots a_{i_{\tau-1} i_{T}} \]
对固定序列 \(I\) ，观测序列 \(O\) 出现的概率 \[ P(O \mid I, \lambda)=b_{i_{1}}\left(o_{1}\right) b_{i_{2}}\left(o_{2}\right) \cdots b_{i_{r}}\left(o_{T}\right) \]
\(O\) 和 \(I\) 同时出现的联合概率 \[ \begin{aligned} P(O, I \mid \lambda) &=P(O \mid I, \lambda) P(I \mid \lambda) \\ &=\pi_{i_{1}} b_{i_{1}}\left(o_{1}\right) a_{i_{1} i_{2}} b_{i_{2}}\left(o_{2}\right) \cdots a_{i_{r-i} i_{T}} b_{i_{T}}\left(o_{T}\right) \end{aligned} \]
对所有可能的状态序列 \(I\) 求和，得观测序列 \(O\) 的概率 \[ \begin{aligned} P(O \mid \lambda) &=\sum_{I} P(O \mid I, \lambda) P(I \mid \lambda) \\ &=\sum_{i_{1}, i_{2}, \cdots, i_{T}} \pi_{i_{1}} b_{i_{1}}\left(o_{1}\right) a_{i_{1} i_{2}} b_{i_{2}}\left(o_{2}\right) \cdots a_{i_{r-i} i_{T}} b_{i_{T}}\left(o_{T}\right) \end{aligned} \]

这种方法的计算量极大，时间复杂度为 \(O(TN^T)\)，这种方法显然是不可行的。

2.2.2. 前向-后向算法

前向-后向算法其实分为两个独立部分——前向算法和后向算法。两种算法求解的方向相反，都能单独地求出一个 \(P(O|\lambda)\) 的表达式，综合两者即可得到一个总的表达式。

两种算法的基本思想都是动态规划。先计算并存储当前时刻每个可能状态的概率值，然后后（前）一时刻的每一个状态的计算都基于前（后）一个时刻，从而减少了重复计算量。时间复杂度都为为 \(O(N^2T)\)

2.2.2.1. 前向算法

定义到 \(t\) 时刻，部分观测序列为 \((o_1,...,o_t)\) 且状态为 \(q_i\) 的概率为前向概率，记作 \[ \alpha_t(i) = P(\alpha_1,...,\alpha_t,i_t=q_i|\lambda) \] 算法流程如下：

计算初值 \[ \alpha_1=\pi_ib_i(o_1) \]
递推 \[ \alpha_{t+1}(i) = \left [ \sum_{j=1}^N \alpha_t(j)a_{ij} \right ] b_i(o_{t+1}) \]
终止 \[ P(O \mid \lambda) = \sum_{i=1}^N \alpha_T(i) \]

2.2.2.2. 后向算法

定义时刻 \(t\) 状态为 \(q_i\) 的条件下，从 \(t+1\) 到 \(T\) 的部分观测序列 \((o_{t+1},...,o_T)\) 的概率为后向概率，记作 \[ \beta_t(i) = P(o_{t+1},...,o_T|i_t=q_i,\lambda) \] 计算流程如下

计算初值 \[ \beta_T(i) = 1 \]
递推 \[ \beta_t(i) = \sum_{j=1}^N a_{ij}b_j(o_{t+1})\beta_{t+1}(j) \]
终止 \[ P(O \mid \lambda)=\sum_{i=1}^{N} \pi_{i} b_{i}\left(o_{1}\right) \beta_{1}(i) \]

最后，综合两式，得最终表达式 \[ P(O \mid \lambda)=\sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{t}(i) a_{i j} b_{j}\left(o_{t+1}\right) \beta_{t+1}(j), \quad t=1,2, \cdots, T-1 \]

2.3. 学习问题

即求解三元组 \((A,B,\pi)\) 使得 \(P(O \mid \lambda)\) 极大化

对于状态序列 \(I\) 是否给定，分为有监督学习和无监督学习两种

2.3.1. 有监督算法

根据三元组的定义，可以直接计算出各值。

设

训练集样本数为 \(S\)
从时刻 \(t\) 的状态 \(i\) 转移到时刻 \(t+1\) 的状态 \(j\) 的频数为 \(A_{ij}\)
状态为 \(j\) 且观测值为 \(k\) 的频数为 \(B_{jk}\)

转移概率 \(a_{ij}\) 的估计为 \[ a_{i j}=\frac{A_{i j}}{\sum_{j=1}^{N} A_{i j}} \] 观测概率 \(b_j(k)\) 的估计值为 \[ b_{j}(k)=\frac{B_{j k}}{\sum_{k=1}^{M} B_{j k}} \] 初始状态 \(\pi_i\) 的估计值为 \[ \pi_k = \frac{\sum_S(i_1=q_k)}{S} \]

2.3.2. 无监督算法

Baum-Welch算法（即EM算法）

2.3.2.1. 两个概率

时刻 \(t\) 处于状态 \(q_i\) 的概率 \[ \begin{aligned} \gamma_{t}(i) &=P\left(i_{t}=q_{i} \mid O, \lambda\right)\\ &=\frac{P\left(i_{t}=q_{i}, O \mid \lambda\right)}{P(O \mid \lambda)}\\ &=\frac{\alpha_{t}(i) \beta_{t}(i)}{\sum_{j=1}^{N} \alpha_{t}(j) \beta_{t}(j)} \end{aligned} \]

时刻 \(t\) 处于状态 \(q_i\) 且在时刻 \(t+1\) 处于 \(q_j\) 的概率

\[ \begin{aligned} \xi_{t}(i, j) &= P\left(i_{t}=q_{i}, i_{t+1}=q_{j} \mid O, \lambda\right) \\ &= \frac{P\left(i_{t}=q_{i}, i_{t+1}=q_{j}, O \mid \lambda\right)}{P(O \mid \lambda)} \\ &=\frac{P\left(i_{t} =q_{i}, i_{t+1}=q_{j}, O \mid \lambda\right)}{\sum_{i=1}^{N} \sum_{j=1}^{N} P\left(i_{t}=q_{i}, i_{t+1}=q_{j}, O \mid \lambda\right)} \\ &=\frac{\alpha_{t}(i) a_{i j} b_{j}\left(o_{t+1}\right) \beta_{t+1}(j)}{\sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{t}(i) a_{i j} b_{j}\left(o_{t+1}\right) \beta_{t+1}(j)} \end{aligned} \]

2.3.2.2. E step

求Q函数 \(Q(\lambda, \bar{\lambda})\) \[ \begin{aligned} Q(\lambda, \bar{\lambda}) &=\sum_{I} \log P(O, I \mid \lambda) P(O, I \mid \bar{\lambda}) \\ &=\sum_{I} \log \pi_{i} P(O, I \mid \bar{\lambda}) +\sum_{I}\left(\sum_{t=1}^{T-1} \log a_{i, i_{t+1}}\right) P(O, I \mid \bar{\lambda})+\sum_{I}\left(\sum_{t=1}^{T} \log b_{i_{t}}\left(o_{t}\right)\right) P(O, I \mid \bar{\lambda}) \end{aligned} \] 其中，\(\bar\lambda\) 为当前模型估计值，\(\lambda\) 为极大化模型后的估计值

2.3.2.3. M step

可以看出Q函数由三部分组成，每一部分未知参数单独存在，故分别对每一个部分单独求极大化即可。

其中，每一部分都可以看做是最值约束问题问题，按照老规矩，都可以使用拉格朗日乘子法解决（公式较多，这里就不列出推导过程，直接给出最终结果，懒~） \[ \pi_{i}=\frac{P\left(O, i_{1}=i \mid \bar{\lambda}\right)}{P(O \mid \bar{\lambda})} \]

\[ \begin{aligned} a_{i j}&=\frac{\sum_{t=1}^{T-1} P\left(O, i_{t}=i, i_{t+1}=j \mid \bar{\lambda}\right)}{\sum_{t=1}^{T-1} P\left(O, i_{t}=i \mid \bar{\lambda}\right)} \\ &= \frac{\sum_{t=1}^{T-1} \xi_{t}(i, j)}{ \sum_{t=1}^{T-1} \gamma_{t}(i)} \end{aligned} \]

\[ \begin{aligned} b_{j}(k) &=\frac{\sum_{t=1}^{T} P\left(O, i_{t}=j \mid \bar{\lambda}\right) I\left(o_{t}=v_{k}\right)}{\sum_{t=1}^{T} P\left(O, i_{t}=j \mid \bar{\lambda}\right)} \\ &= \frac{\sum_{t=1, o_{t}=V_{k}}^{T} \gamma_{t}(j)}{\sum_{t=1}^{T} \gamma_{t}(j)} \end{aligned} \]

2.3.2.4. 最终流程

初始化 \(\lambda^{(0)} = (A^{(0)}, B^{(0)}, \pi^{(0)})\)
递推。 \[ a_{ij}^{(n+1)}= \frac{\sum_{t=1}^{T-1} \xi_{t}(i, j)}{ \sum_{t=1}^{T-1} \gamma_{t}(i)} \]

\[ b_j(k)^{(n+1)} = \frac{\sum_{t=1, o_{t}=V_{k}}^{T} \gamma_{t}(j)}{\sum_{t=1}^{T} \gamma_{t}(j)} \]
终止。得模型参数 \(\lambda^{(n+1)} = (A^{(n+1)}, B^{(n+1)}, \pi^{(n+1)})\)

2.4. 预测问题

也称HMM的解码，求给定条件概率 \(P(I \mid O)\) 的最大状态序列 \(I\)

2.4.1. 近似算法

采用贪心算法的思想，计算在每个时刻 \(t\) 选择该时刻最有可能出现的状态 \(i_t'\)，即 \[ i_{t}'=\arg \max _{1 \leqslant i \leqslant N}\left[\gamma_{t}(i)\right] \] 该算法只能得到局部最优解，而且有可能得到实际中不可能出现的状态序列，例如，转移概率为0的相邻状态。

2.4.2. 维特比算法

采用动态规划的思想，求概率最大路径（最优路径）。

计算过程如下：

初始化 \[ \delta_1 = \pi_i b_i(o_1) \]

\[ \Psi_1(i)= 0 \]
递推 \[ \delta_t(i) = \max_{1\leq j \leq N} [\delta_{t-1}(j)a_{ji}]b_i(o_t) \]

\[ \Psi_t(i) = \arg \max_{1\leq j \leq N} [\delta_{t-1}(j)a_{ji}] \]
终止 \[ P = \max_{1 \leq i \leq N} \delta_T(i) \]

\[ i_T = \arg \max _{1 \leq i \leq N} [\delta_T(i)] \]
最优路径回溯 \[ i_t = \Psi_{t+1} (i_{t+1}) \]