1. 基本定义

正则项一般用于线性的回归或分类模型，一般认为其可以减轻模型过拟合的程度。

首先给出模型的目标函数为 \[ J(\theta) = L(\theta) + \lambda \Phi(\theta) \] 其中，\(L(\theta)\) 为损失函数，\(\lambda\) 为正则化系数，\(\Phi(\theta)\) 为正则化函数，其一般是一个过原点的凸函数。

下面从两个角度来看正则项的作用

1.1. 降低复杂程度

模型越是复杂对样本的拟合程度越高，要减轻过拟合程度，即降低模型的复杂程度，或者更加专业的说法是结构风险最小化。

我们不妨假设 \(L(\theta)\) 是一个关于 \(\theta\) 的只有一个最优解的凸函数，将 \(L(\theta)\) 和 \(\Phi(\theta)\) 的等高线图分别表示在同一张图中，于是得到下面这张经典的图

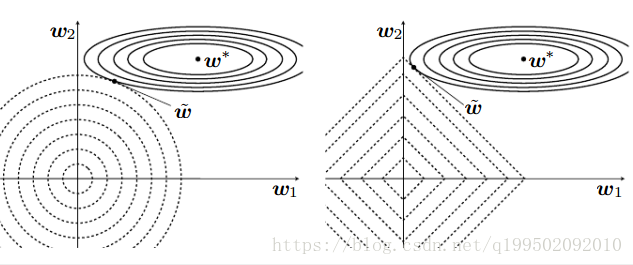
图中的 \(w\) 即为本文中的 \(\theta\)，左图中 \(\Phi(\theta)\) 为 \(L_2\) 正则，右图为 \(L_1\) 正则

在不加正则项的情况下，模型的最优解应该在损失函数的中心点处。加了正则项后，模型的目标函数为损失项和正则项之和，可以看出，当损失项增大时，正则项减小；损失项减小时，正则项增大。两者相互制约。

于是，可以将 \(\Phi(\theta)\) 看做一个约束项（其实从正则的英文中可以看出，正则就带有规则的意思，所以正则项就是对函数添加的一个约束规则项），目标函数可以改写为 \[ \begin{array}{ll} \min_{\theta} &\quad L(\theta) \\ \text{s.t.} &\quad \Phi(\theta) < C \end{array} \] 约束项的作用是将目标函数的最优解往原点方向拉近，从而使模型权值越趋向于0，对于线性模型来说，这意味着对应特征对系统输出的影响越小。所以减小模型权值，意味着降低了模型的复杂程度，从而减轻了模型过拟合程度。

这里顺便再简单地找出最优解的位置。

我们将两个函数分别看成两个最优化问题，则在最优解的等高线处，两个函数的下降的梯度应该相反且在同一直线上，大小也应该相等，而这点为两函数等高线的切点处。可以将其想象在该点处，相互作用的力达到平衡。

但是不符合以上条件的并非一定不是最优解，我们不妨再假设 \(L(\theta)\) 是平行于 \(\theta\) 坐标轴的平面，此时找不到符合上面规律的交点，但此时最优解位置是在原点，而且此时系统的最优解已经不依赖于 \(L(\theta)\) 而只依赖于 \(\Phi(\theta)\) 了，这岂不是喧宾夺主了？

虽然上面这个例子有点极端，但也反映了正则项不一定都能对系统进行优化，也有可能产生副作用，所以正则项是非必要的，一般要配合数据以及算法特性使用。按照经验，如果样本数量小于模型参数的10倍，则说明模型具有过拟合的可能性，则可以无脑加上 \(L_1\) 或 \(L_2\) 正则项。

1.2. 减小模型方差

高偏差（bias）会导致欠拟合，高方差（variance）会导致过拟合。要减轻过拟合程度，即降低模型的方差。

偏差即模型对训练集的预测误差，这个我们已经用损失函数进行体现。

方差是模型的训练误差和验证误差的差距。对于不同的输入样本，损失函数的值也会不一样，但正则项是一个只关于 \(\theta\) 的函数，不同输入样本的正则项的值是一样的，即可以将其看做一个常数项。

不妨设训练集的输出损失函数为 \(l_1\)，验证集的输出损失函数为 \(l_2\) ，一般有 \(l_1 > l_2\) ，两者的正则项为 \(\delta>0\)，则模型的训练误差和验证误差的差距可以简单计算为 \(\frac{l_1 - l_2+\delta}{l_1+\delta} < \frac{l_1-l_2}{l_1}\)。可以看出加了正则项后，相当于对损失函数做了平滑处理，减小了训练误差和验证误差的差距，从而减轻了模型过拟合的程度。

2. \(L_p\) 正则

\(L_p\) 已经多次被提到过了，已经是我们的老朋友了，这里再全面总结一下。

正则项如果用到了p-范数就称其为 \(L_p\) 正则。范数一般分为向量范数和矩阵范数

2.1. 向量范数

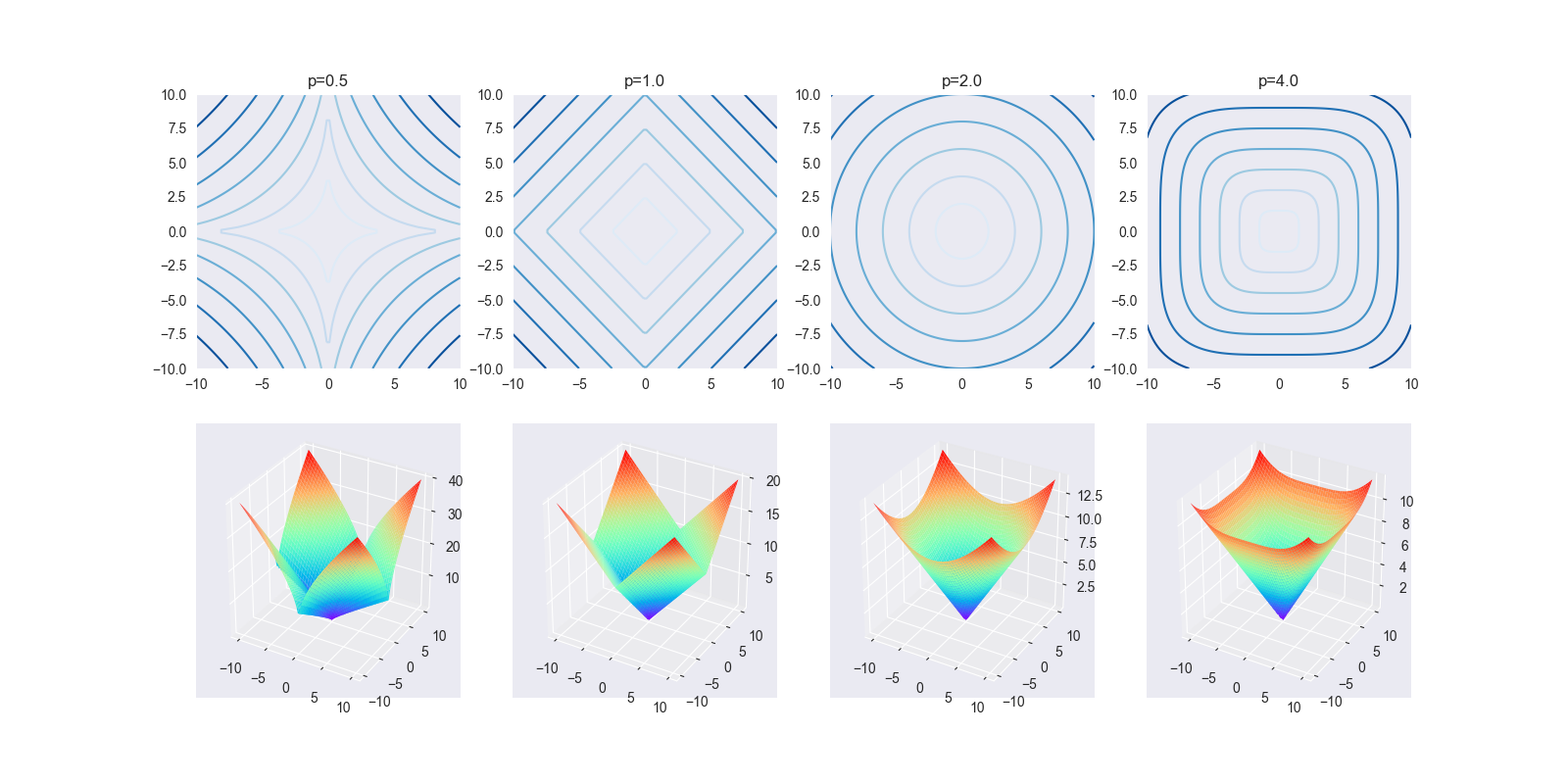
下面给出其一般表达式 \[ \|x\|_p = (\sum_{i=1}^n |x_i|^p)^{\frac{1}{p}},x\in R^n \] 下面给出常见范数的现实意义

0范数，向量中非零元素的个数。
1范数，为绝对值之和。
2范数，就是通常意义上的模。
\(\pm\infty\) 范数，即求向量元素绝对值中的最值，即 \(\|x\|_{-\infty}=\arg \min_i |x_i|,\|x\|_{+\infty}=\arg\max_i|x_i|\)

下面给出常见范数等高线图和3D函数图

从上面可以看出，随着p越大，等高线图越接近正方形（正无穷范数）；越小，曲线弯曲越接近原点（负无穷范数）

一定程度上反映了，当p值越小，则最优解越容易趋近于某个坐标轴，意味正交于该坐标轴的权值趋向于0，即所谓的参数稀疏化；当p值越大，则约束项~~对各个维度的权值约束力趋于相同~~（待证明），则最终的效果为~~等比例~~地缩小各个权值。

2.2. 矩阵范数

1-范数，列和范数（列模），即所有矩阵列向量绝对值之和的最大值 \[ \|X\|_p = \max_{1\leq j \leq n} \sum_i^m |x_{ij}| , X \in R^{m\times n} \]
2-范数，谱范数（谱模） \[ \|X\|_2=\sqrt{\max_{1\leq i \leq n} |\lambda_i|} \] 其中 \(\lambda_i\) 为 \(X^T X\) 的特征值
\(+\infty\)-范数，行和范数（行模），即所有矩阵行向量绝对值之和的最大值 \[ \|X\|_p = \max_{1\leq i \leq n} \sum_j^m |x_{ij}| \]
F-范数，Frobenius范数，即矩阵元素绝对值的平方和再开平方 \[ \|X\|_p = (\sum_i^m\sum_j^n x_{ij})^{\frac{1}{2}} \]
核范数 \[ \|X\|_* = \sum_i^n \lambda_i \] 其中，如果X矩阵是方阵，\(\lambda_i\) 称为本征值。若X不是方阵，\(\lambda_i\) 称为奇异值，即奇异值/本征值之和