1. 输入输出

Input:

样本空间 \[ X= \{x_1, x_2, ..., x_N\},x_i \in \mathbb{R}^n \] 先验参数 \((\epsilon,MinPts)\)

Output:

样本空间中每个点的预测类别 \[ Y=\{y_1,y_2,...,y_{N}\},y_i \in \{0,1,...,k\} \] 类簇集合 \[ C=\{C_1,C_2,...C_k\},C_i=\{x \in X | y = y_i \} \]

2. 模型效果

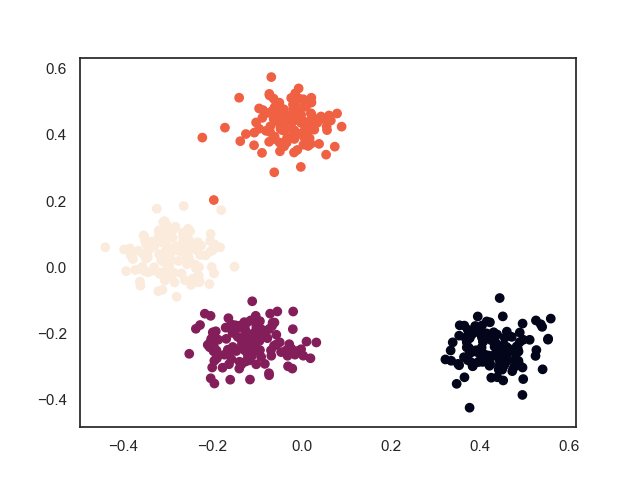
2.1. 训练效果

上面过程中可以看出，与层次聚类算法“雨后春笋”般的聚类过程不一样，DBSCAN算法的聚类过程是“拉帮结社”式地进行，总是将范围内紧密联系的样本点连接在一团，然后团与团之间再进行兼并。

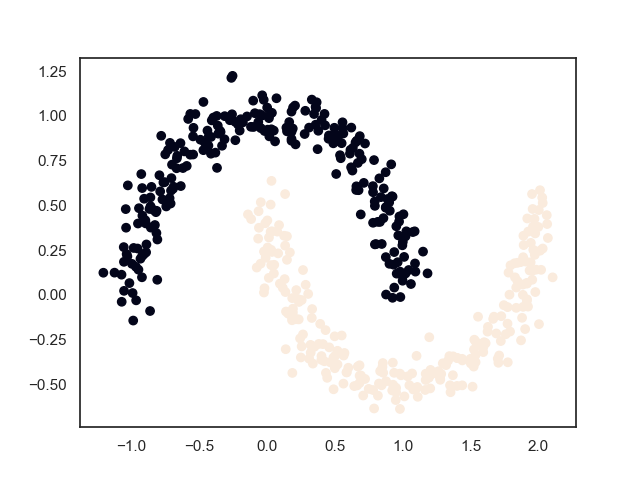
2.2. 最终结果

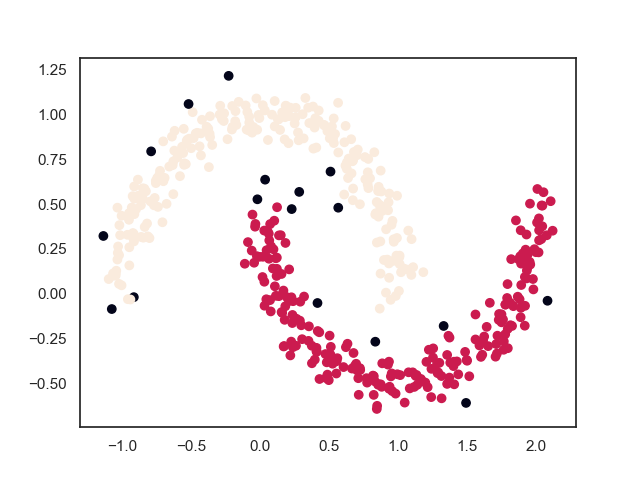
3. 相关概念

\(\epsilon\) 邻域，对于任意一点 \(x_j\) ，该点的 \(\epsilon\) 邻域定义为样本空间间所有与 \(x_j\) 的距离不大于 \(\epsilon\) 的样本，即 \(N_{\epsilon}(x_j) = \{ x_i \in X|dist(x_i, x_j) \leq \epsilon \}\)
密度，\(x\) 的 \(\epsilon\) 邻域的样本的数量，即 \(\rho(x) = |N_{\epsilon}(x)|\)
核心点（core point），\(\rho(x) \geq MinPts\) 的样本点
边界点（border point），\(\rho(x) < MinPts\) 且 \(x\) 落在任意一个核心点的 \(\epsilon\) 邻域的样本点
噪声点（noisy point），既非核心点也非边界点的样本点
密度直达，\(x_j\) 位于 \(x_i\) 的 \(\epsilon\) 邻域中，且 \(x_i\) 为核心点，则称 \(x_j\) 由 \(x_i\) 密度直达
密度可达，对 \(x_j\) 和 \(x_i\) ，若存在一系列点 \(p_1,...,p_n\) ，使得 \(p_1=x_i,p_n=x_j\) ，且 \(p_{i+1}\) 由 \(p_i\) 密度直达，则称 \(x_j\) 由 \(x_i\) 密度可达
密度相连，对 \(x_j\) 和 \(x_i\) ，若存在 \(x_k\) ，使得 \(x_j\) 和 \(x_i\) 均由 \(x_k\) 密度可达，则称 \(x_j\) 和 \(x_i\) 密度相连

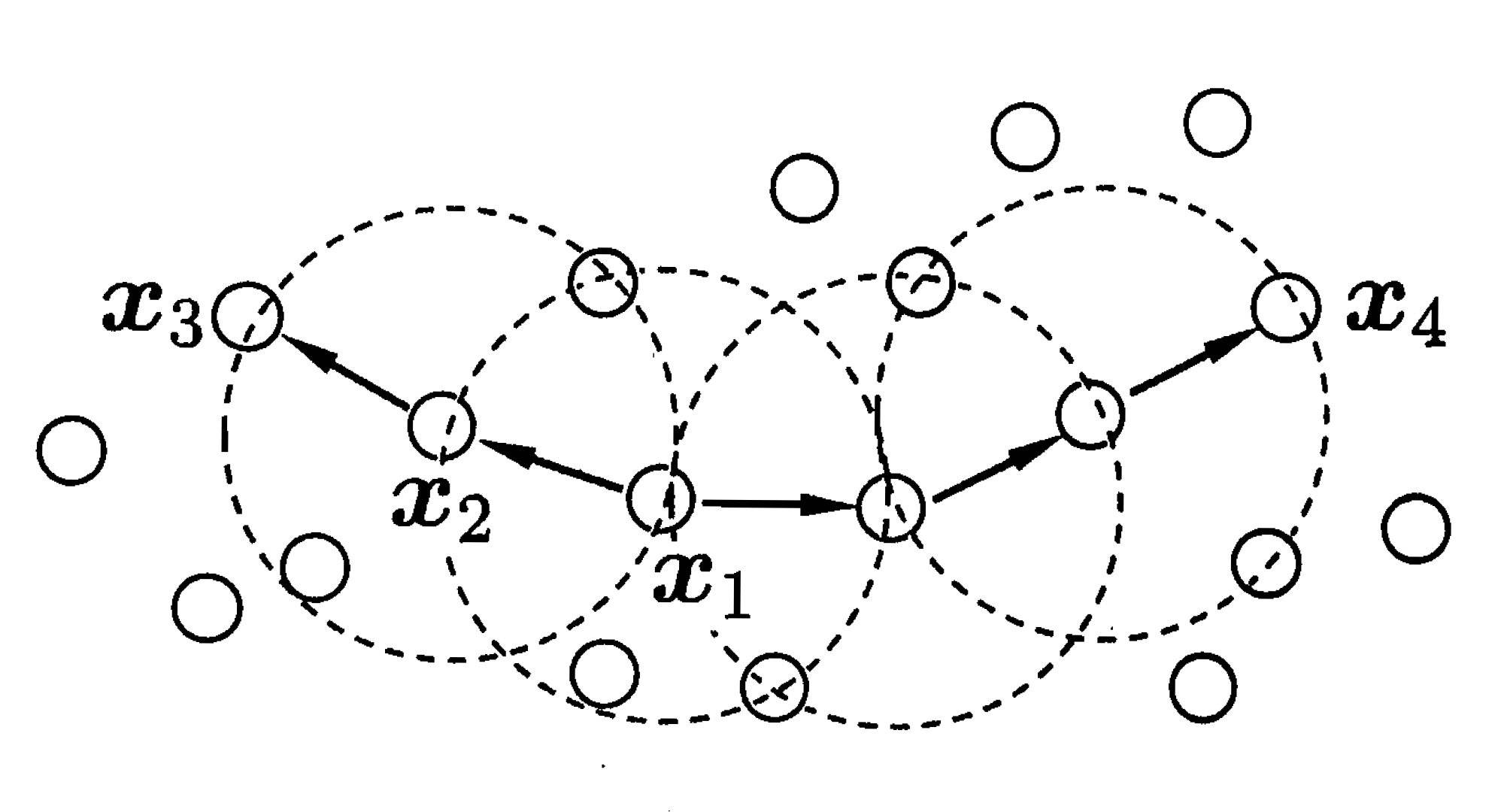
下图形象地给出上面各种概念

其中，\(MinPts=3\)，虚线部分为对应中心点的 \(\epsilon\) 邻域，\(x_2\) 由 \(x_1\) 密度直达，\(x_3\) 由 \(x_1\) 密度可达，\(x_3\) 和 \(x_4\) 密度相连

4. 学习算法

DBSCAN算法的核心思想是从某个核心点出发，不断向密度可达的区域扩张，从而得到一个包含核心点和边界点的最大化区域，区域中任意两点密度相连。

关于该算法的核心思想的描述，还有一个形象生动的有趣比喻：将其类比成诸侯分封的过程。

样本空间中的每一个点看作是奴隶社会中的一个士人（point）。

当一个士人的势力范围（\(\epsilon\)邻域）中的其他士人的数量超过一定的数量（MinPts）时，士人便发展成为一个士族（core point）；如果一个士人的势力范围内其他士人的数量没有超过阈值，但其属于其他士族的管辖范围内（依附于其他士族）时，则将其作为该士族的门客（border point）；既不是士族也不是门客的士人则成为游离的说客（noisy point）

多个关系紧密的士族联合在一起便形成了一个诸侯国（class），所有诸侯国便组成了一个天下（sample space）

具体的算法流程如下：

Init:

计算每个样本点 \(x_i\) 的 \(\epsilon\) 邻域 \(N_\epsilon(x_i)\)
初始化每个样本点 \(x_i\) 的类别标签 \(y_i=i\)

Repeat:

样本空间中的任意一点 \(x_i\)，如果 \(\rho(x_i) \geq MinPts\) ，则将其归为核心点；反之，则跳过这次循环
寻找核心点 \(x_i\) 对应的簇 \(C_i=\{x \in X|y = y_i\}\)
对核心点 \(\epsilon\) 邻域中的每个样本点 \(x_j\) ，寻找其对应的簇 \(C_j=\{x \in X|y = y_j\}\)，合并 \(C_i\) 和 \(C_j\) ，更新 \(C_j\) 中样本的标签为 \(\{y=y_i|x \in C_j \}\)（在更新的过程中，既包括核心点也包括了边界点）

Until: 所有的样本点都遍历一遍

End:

将非核心点或边界点的样本点归为噪声点，即将其标志值置为 \(-1\)
对输出标签重新排序编号

算法的时间复杂度为 \(O(N^2)\) ，资源主要消耗在初始化计算 \(\epsilon\) 邻域上，其本质思想为求最近邻，参考KNN算法，可以加入kd树或球树进行优化。

5. 参数确定

这个算法有两个非常重要的先验参数 \((\epsilon,MinPts)\) 需要确定，但因为样本空间的数据分布、数据维度等不一样，这两个参数并没有推荐的取值范围，而且往往也是很难去确定的。下面介绍一种我常用的方法：

计算 \(x_i\) 对其他样本的距离，并从小到大排序得到距离序列 \(d_i= \{d_{i,1}, ..., d_{i,N}\}\) ，取所有样本（如果样本数量较多时取部分样本）距离序列的第 \(2MinPts\) 个距离值的均值（如果噪声值过多或者与真实值相差较大时，取中位值）作为 \(\epsilon\) 值，即 \[ \epsilon = \frac{1}{N} \sum_{i=1}^N d_{i,2MinPts} \] 这种做法可以保证绝大多数点不会被归为噪声值，同时也在一定程度上保留模型排除噪声点的能力。

而 \(MinPts\) 一般取较小的值，sklearn中建议的默认取值为5，所以可以在5上下取值进行尝试。