1. 输入输出

训练输入： \[ T=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中，

\(x\) 为特征域，\(x_i \in \mathbb{R}^{n},i =1,2,...,N\)
\(y\) 为标签域，\(y_i \in \{c_1,\cdots,c_K\}\) ，\(K\) 为输出标签集合大小。

测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^n \] 测试输出： \[ Y'=\{y'_1,\cdots,y'_{N'}\},y_i' \in \{c_1,\cdots ,c_K\} \]

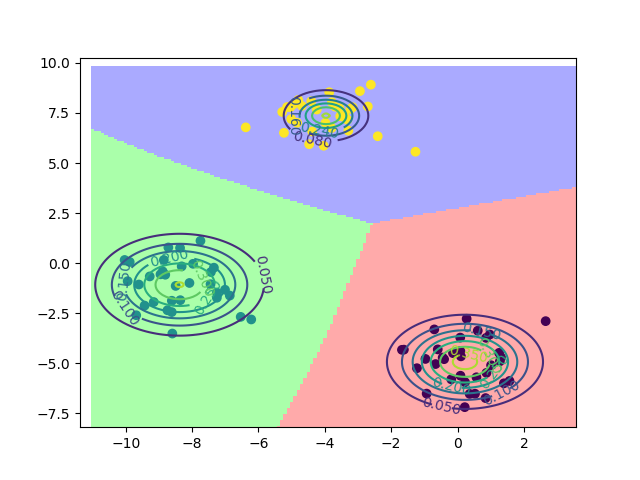
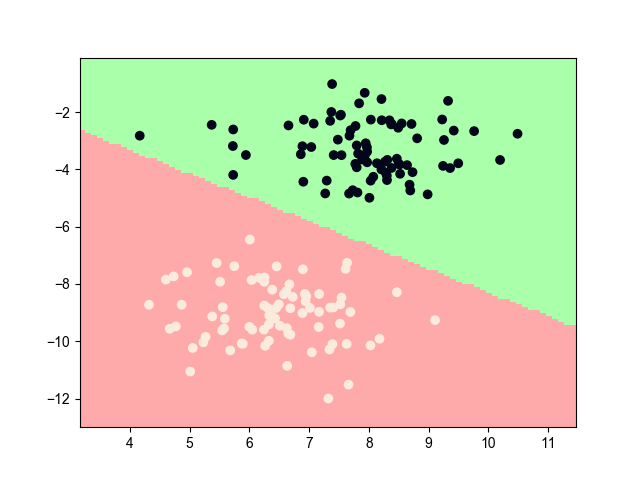
2. 模型效果

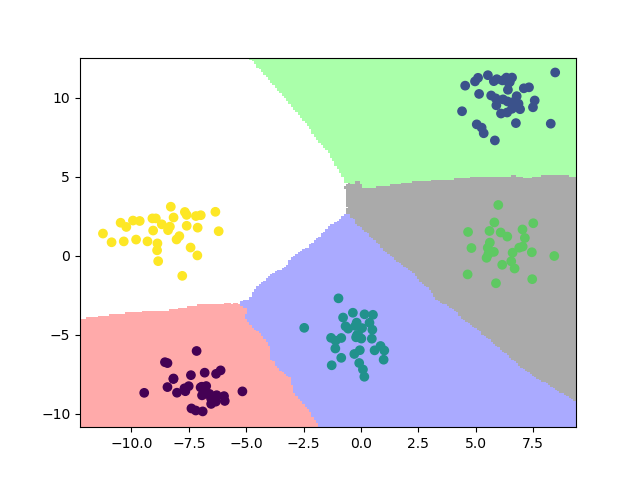
3. 模型推导

3.1. 基本方法

由于KNN是典型的lazy learning算法，不存在训练过程，只有当预测的时候才会进行“学习”。故直接看测试集的预测过程即可。

模型预测也相当简单，对于输入的测试样例 \(x\)，计算其与训练中所有点的距离，筛选出距离距离最近的前 \(k\) 个点，记为 \(N(k)\)。统计 \(N(k)\) 中出现次数最多的类别 \(y\)，作为测试样例的预测值。即模型的函数为 \[ f(x)=\arg \max_{c_j} \sum_{x_i \in N_k(x)} I(y_i=c_j),i=1,2,...,N;j=1,2,...,K \]

3.2. 距离函数选择

3.2.1. \(L_p\) 距离（Minkowski距离）

\[ L_p(x_i,x_j)=(\sum_{l=1}^n |x_i^{(l)}-x_j^{(l)}|^p)^{\frac{1}{p}} \]

\(p=2\) 时为 \(L_2\) 距离，即欧氏距离
\(p=1\) 时为\(L_1\) 距离，即曼哈顿距离
\(p= \infty\) 时为各个坐标距离的最大值

该距离函数体现了数值上的绝对差异

3.2.2. 余弦距离

\[ \cos(\theta) = \frac{\sum_{i=1}^n A_i B_i}{\sqrt{\sum_{i=1}^n A_i^2 \cdot \sum_{i=1}^n B_i^2}} \]

该距离函数体现方向上的相对差异

3.3. k值选择

k值较小，“学习”的近似误差变小，但对噪声点敏感，意味着整体模型变得复杂，容易过拟合

k值较大，减少“学习”的估计的误差，但近似误差也会变大，模型很可能学不到东西，意味着整体模型变得简单。

如果模型较简单，就会忽略训练集中大量有用的信息，所以两者权衡下，应取较小的k值。通常使用交叉验证法来选取最优的k值。

3.4. 搜索算法优化

如果采用上面的线性扫描的方法，当k远小于N时，许多点的计算是没用的。为了减少计算次数，提高搜索效率，提出了kd树的存储结构。

kd树是一棵二叉树，对于输入 \(x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(l)})\) ，构建流程如下：

选取 \(x_i^{(1)}\) 作为划分坐标轴，并寻找其中位数，将该点作为主节点，小于切分点的划分到做节点区域，反之，则划分到右节点区域
选取 \(x_i^{(2)}\) 作为划分坐标轴，分别对左右区域重复步骤1的划分方法
一直选取下一坐标轴，如果到了 \(x_i^{(l)}\)，则重新从 \(x_i^{(1)}\) 开始，直到所有的区域只有一个点，则kd树构建完毕

特别地，划分点不一定需要选取中位数，选取中位数并不会提高搜索的效率，但会提升空间的存储的效率，因为这样得到的二叉树是平衡的。

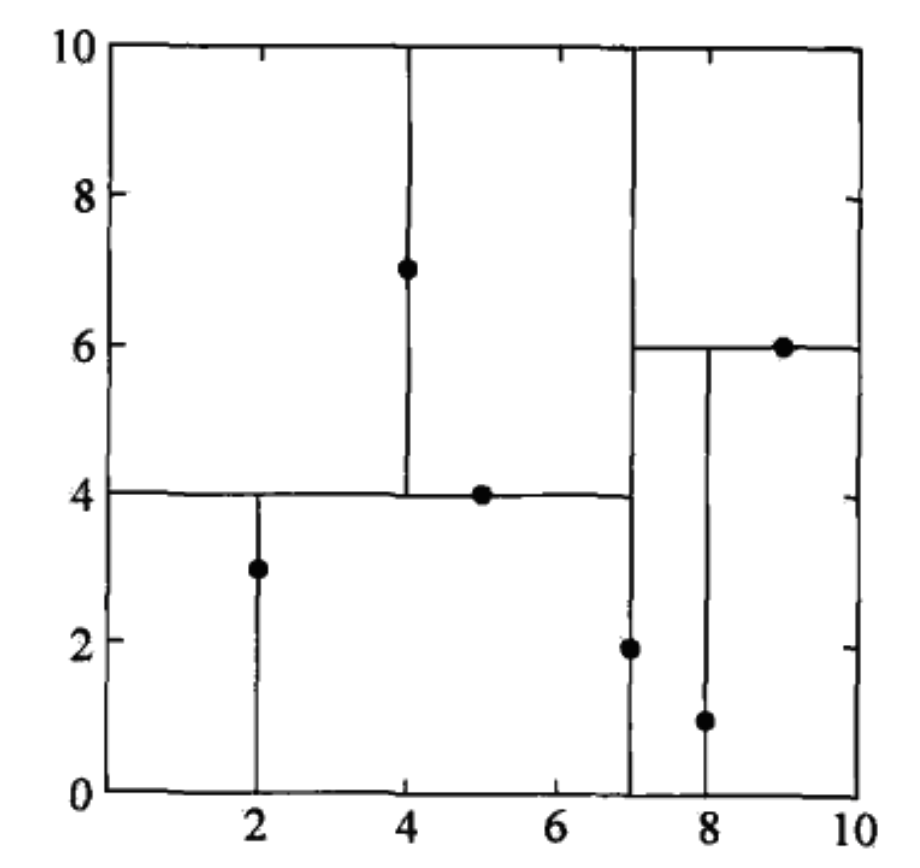
一棵建成的kd树样例如下：

对于输入测试样例 \(x\)，k近邻的搜索流程如下：

kd树中找到包含 \(x\) 的叶子节点（\(x\) 当前维的坐标小于当前节点的坐标，则 \(x\) 包含在当前节点的左节点区域，反之，则包含在当前节点的右节点区域），计算 \(x\) 和叶子节点的距离。
如果 \(N(k)\) 的元素的数量小于 \(k\) ，则直接加入当前节点，或当前距离小于\(N(k)\) 中的最大距离，则去掉\(N(k)\) 中距离最大的点，加入当前节点。
递归向上回退，将当前节点的父节点作为当前节点。
计算当前节点与 \(x\) 的距离，重复步骤2；判断当前节点的子节点的区域是否与 \(x\) 相交（如果 \(x\) 当前维的坐标与当前节点的当前维坐标的差值小于小于\(N(k)\) 中的最大距离，则 \(x\) 与当前节点的左子节点的区域相交；如果当前节点的当前维坐标与 \(x\) 当前维的坐标的差值小于小于\(N(k)\) 中的最大距离，则 \(x\) 与当前节点的右子节点的区域相交），如果相交，则该将子节点作为当前节点，重复步骤4，反之，则重复步骤3-4，直到回退至根节点， \(N(k)\) 即为k近邻点集。