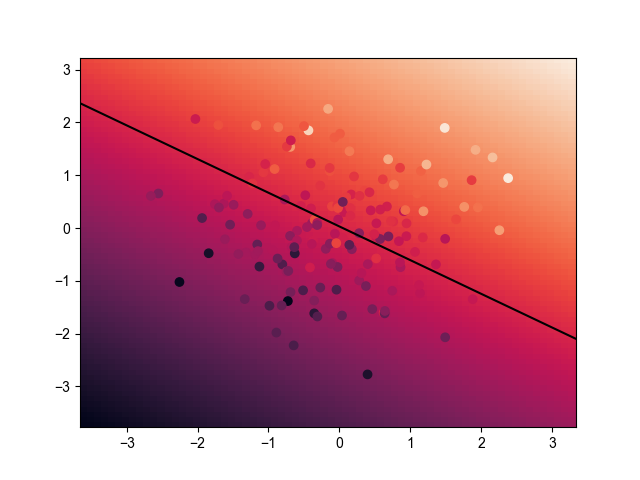
决策树(Decision Tree)是一种基于信息熵的分类算法(准确来说,这是一种数据结构)
基于numpy的实现代码传送门
1. 输入输出
训练输入: \[ D=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中,
- \(x\) 为特征域,\(x_i \in \mathbb{R}^{n},i =1,2,...,N\)
- \(y\) 为标签域,\(y_i \in \{c_1,\cdots,c_K\}\) ,\(K\) 为输出标签集合大小。
测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^n \] 测试输出: \[ Y'=\{y'_1,\cdots,y'_{N'}\},y_i' \in \{c_1,\cdots ,c_K\} \]
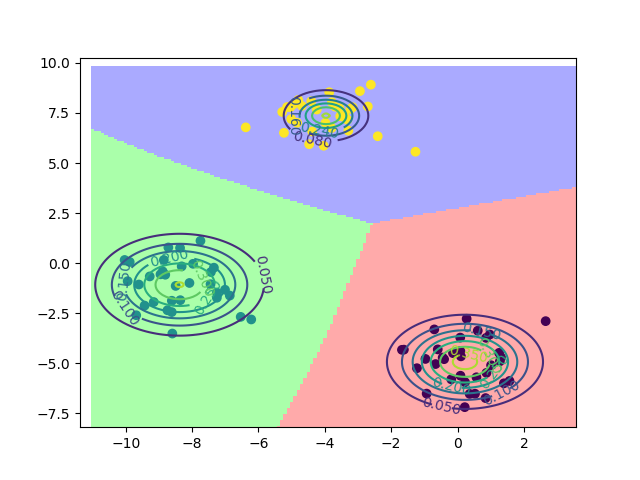
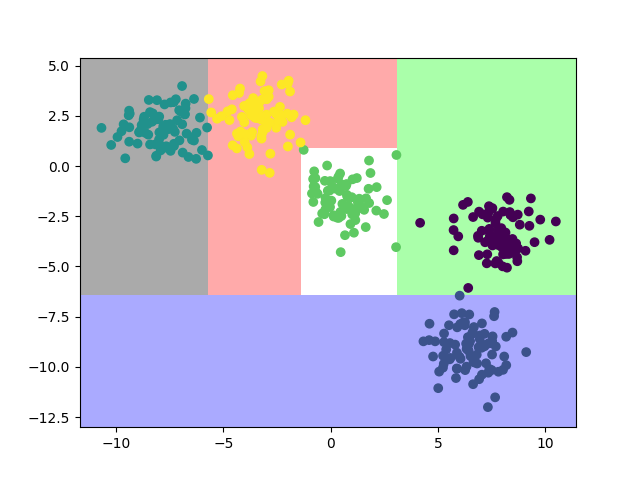
2. 模型效果
| ID3 | C4.5 | CART | |
|---|---|---|---|
| 分类效果 | 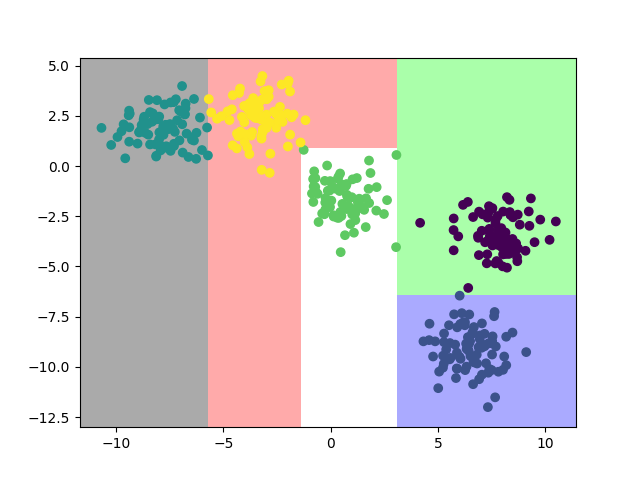 |
 |
 |
3. 模型推导
3.1. 基本方法
书中一般以离散型数据作为例子讲解,因为这样讲解清晰易懂,但先不说实际运用中大部分输入为连续型,即便是离散型数据,构建树的时候需要按照每个特征值创建一个节点,实际中的数据的特征值一般都是很多的,这显然不太合理。实际上,离散型的数据都是以数值型作为输入,故为了构建和遍历方便,可以把所有的输入数据当做连续性处理,对应生成的决策树是一棵二叉树,其一般构建流程如下
- 设立一个阈值 \(\varepsilon\);创建一个根节点,并将其作为当前节点;将输入特征域 \(X\) 作为 \(D\)
- 如果到达最大递归深度,则递归返回;如果 \(D\) 所有实例都属于同一类,则将当前节点作为叶节点,并将 \(D\) 中实例数最大的类 \(C_k\) 作为当前节点的标签,递归返回;否则,进行下一步
- 计算 \(D\) 每个特征的特征选择准则,选择增益最大的特征 \(A_g\)
- 如果 \(A_g < \varepsilon\) ,则将当前节点作为叶子节点,并将 \(D\) 中实例数最大的类 \(C_k\) 作为当前节点的标签
- 否则,将 \(D\) 划分成数个节点(这一步需要判断 \(D\) 是否为空集,如果是空集则不创建对应的节点,并递归返回),并分别将对应的区域作为 \(D\),对应的节点作为当前节点,取 \(D\) 中实例数最大的类 \(C_k\) 作为当前节点的标签,然后递归地重复步骤2~5
现在问题只剩下如何计算特征选择准则以及节点的划分准则了,请看下节
3.2. 特征选择
注意,下面提到的算法和一般书上描述的不完全一样,书上描述的算法可分为特征选择和节点划分两部分,这里只保留了前者,因为后者各个算法间是可以互用的,例如,C4.5算法和CART算法的节点划分方法完全可以应用于ID3算法中,使得ID3算法也能用于连续型数据
3.2.1. ID3
ID3算法以信息增益作为特征选择准则
信息增益的计算基于大名鼎鼎的香农信息熵,设所有可能事件可能发生的概率集合为 \(\{p_1, ..., p_n\}\),则其信息熵为 \[ H(X) = - \sum_{i=1}^n p_i \log p_i \] 其中,当 \(p_i=0\)时,\(p_i \log p_i = 0\)
特别地,当 \(\log\) 是以2为底时,其单位为bit;以e为底时,其单位为nat
又 \(H(X)\) 仅依赖于X的分布,而与X的具体取值无关,所以也常将其记为 \(H(p)\)
取值范围:\(0 \leq H(X) \leq \log n\)
基于此,我们可以推导出以下计算公式
数据集 \(D\) 的经验熵为 \[ H(D)= - \sum_{k=1}^K P(D_k) \log P(D_k) \] 其中 \[ P(D_k)= \frac{|C_k|}{|D|} = \frac{\sum_{i=1}^N I(y_i=c_k)}{N} \] 特征 \(A\) 对 \(D\) 的经验条件熵为 \[ H(D|A) = \sum_{i=1}^n \frac{|D_i|}{|D|} H(D_i) \\ H(D_i) = -\sum_{k=1}^K \frac{|D_{ik}|}{|D_i|} \log \frac{|D_{ik}|}{|D_i|} \] 其中,\(D_i\) 使用对应准则划分的关于 \(D\) 的子集,
最终,计算出各个特征的信息增益为 \[ g(D,A)=H(D)-H(D|A) \] 选择增益最大的特征
3.2.2. C4.5
C4.5算法和ID3算法类似,但前者使用信息增益比替代信息增益(统计学习方法第一版时采用的方法) \[ g_R(D,A) = \frac{g(D,A)}{H(D)} \] 或者(统计学习方法第二版时采用的方法) \[ g_R(D,A) = \frac{g(D,A)}{H_A(D)} \] 其中 \[ H_A(D) = - \sum_{i=1}^n \frac{|D_i|}{|D|} \log \frac{|D_i|}{|D|} \]
实际上,增益比就是对增益的“归一化”,这样做的好处是克服了ID3的只用信息增益作为特征选择和节点分支的唯一标准,但这一特征可能并不会提供太大用的信息量,C4.5算法对此进行校正,重新给出特征的信息量。
3.2.3. CART
CART算法以基尼指数作为特征选择准则
基尼指数的计算公式如下 \[ \text{Gini}(p) = 1-\sum_{k=1}^K p_k^2 \] 对于二分类问题,如果标签为1的类的概率为 \(p\),则基尼指数可以简化为 \[ \text{Gini}(p) = 2p(1-p) \] 基尼指数表示一个集合的不确定性,类似于熵,后面为了描述方便,直接把该值“等价于”信息熵
集合 \(D\) 的基尼指数为 \[ \text{Gini}(D) = 1-\sum_{k=1}^K (\frac{|C_k|}{|D|})^2 \] 特征 \(A\) 条件下,集合 \(D\) 的指数为 \[ \text{Gini}(D,A) = \sum_i^n \frac{|D_i|}{|D|}\text{Gini}(D_i) \] 为了跟前面的特征选择依据一致,取 \(-\text{Gini}(D,A)\) 值最高的特征作为选择的特征
3.3. 子树划分
3.3.1. 按每个特征划分
对于输入离散型数据,一般书上用到的方法为每一个特征值划分为一个子树
设 \(x_j\) 所有可能取值的集合为 \(\{a_1,...,a_n\}\) ,则 \[ D_i=D_{x_j=a_i} \\ |D_i|=\sum_{l=1}^N I(x_{lj}=a_i) \\ |D_{ik}|=\sum_{l=1}^N I(x_{lj}=a_i,Y=c_k) \]
3.3.2. 按信息量最大的特征划分
上面的划分方法有个问题,当特征值很多的时候,就会被划分成很多棵子树,当然可以通过后面的减枝的方法进行优化,但现在也一种折中的划分方法——将决策树转化为一棵二叉树。这种方法用宽度换取长度,是相当合算的。
按选择的特征列每个特征值 \(a_i\),选择如下划分的策略中的一种将 \(D\) 划分为两个子集 \(D_1\) 和 \(D_2\)
对于非数值型特征,必须以是否与 \(a_i\) 相等进行划分,此时 \[ D_1 = D_{x_j=a_i}, D_2 = D_{x_j \neq a_i} \]
对于数值型特征,可以采用与 \(a_i\) 的大小比较进行划分,此时 \[ D_1 = D_{x_j \leq a_i}, D_2 = D_{x_j > a_i} \]
计算每个特征的信息增益 \(g(D_{1,2},A_i)\) 或负基尼系数 \(-Gini(D_{1,2},A_i)\),
选择增益值最大的特征 \(a_i\) 作为划分点
3.3.3. 按中位值划分
对于连续型数据输入,将特征 \(A\) 升序排序得到集合 \(\{a_1,...,a_n\}\) ,然后计算两个相邻的特征的中位值 ,形成新的集合 \(A' = \{a_1',...,a_{n-1}'\} = \{ (a_i + a_{i+1})/2|i=1,...,n \}\) ,使用 \(A'\) 代入按信息量最大的特征划分中计算即可。
4. 剪枝
为了解决过拟合问题,需要对决策树 \(T\) 进行简化
设决策树学习的损失函数为 \[ C_{\alpha}(T) = C(T) + \alpha |T| = \sum_{t=1}^{|T|} N_t H_t(T) + \alpha |T| \] 其中, \(C(T)\) 表示模型对训练数据的测试误差,即拟合程度, \(|T|\) 为树的节点个数,表示模型的复杂度,每个叶节点样本数为 \(N_t\),\(\alpha \geq 0\) 为控制参数,\(\alpha = 0\) 表示只考虑模型拟合程度,不考虑复杂度
经验熵 \[ H_t(T) = -\sum_{k} \frac{N_{tk}}{N_t} \log \frac{N_{tk}}{N_t} \] 其中,\(N_{tk}\) 为 \(k\) 类样本的样本数
剪枝就是当 \(\alpha\) 确定时,选择损失函数最小的模型,距离流程如下
- 计算每个节点的经验熵
- 递归地从树的叶节点往上回缩,设回缩到父节点之前与之后的损失值为 \(C_{\alpha}(T_B)\) 和 \(C_{\alpha}(T_A)\),如果 \(C_{\alpha}(T_A) \leq C_{\alpha}(T_B)\),则将该父节点变成新的叶子节点
- 遍历下一个叶节点,重复执行步骤2,直到所有的叶节点遍历结束为止
5. references
《统计学习方法》第5章,李航
《机器学习》第4章,周志华
To be continue~