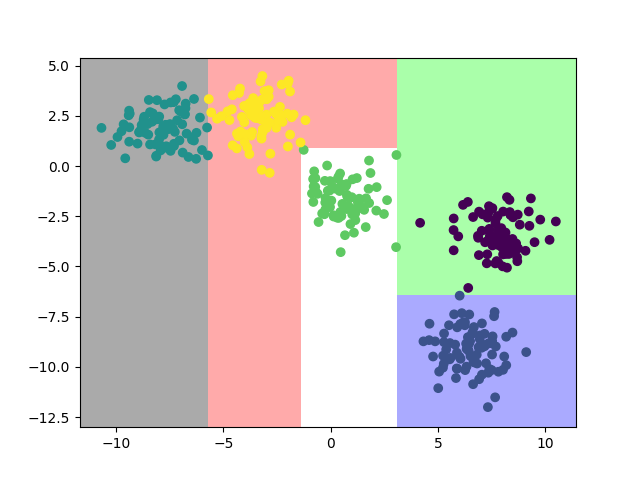
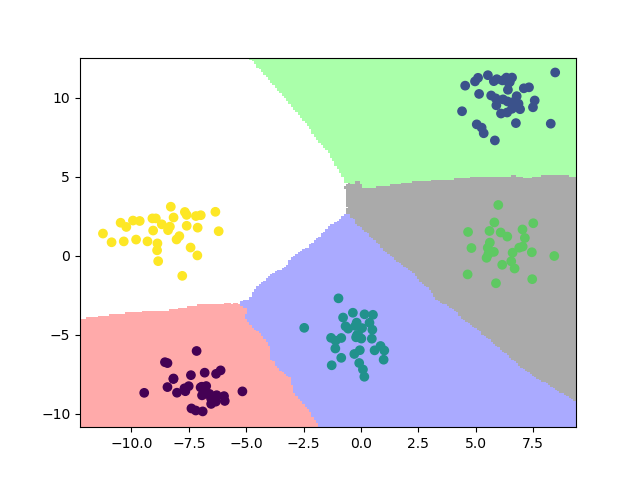
朴素贝叶斯法(Naive Bayes)是一种基于概率统计的分类算法。
基于numpy的实现代码传送门
1. 输入输出
训练输入: \[ T=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中,
- \(x\) 为特征域,\(x_i \in \mathbb{R}^{n},i =1,2,...,N\)
- \(y\) 为标签域,\(y_i \in \{c_1,\cdots,c_K\}\) ,\(K\) 为输出标签集合大小。
测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^n \] 测试输出: \[ Y'=\{y'_1,\cdots,y'_{N'}\},y_i' \in \{c_1,\cdots ,c_K\} \]
2. 模型推导
朴素贝叶斯算法可以算是基于贝叶斯理论的入门算法,总体而言是比较简单的。
贝叶斯相关理论可参考:常用概率统计基础
概率密度函数相关的知识可参考:常用概率分布
2.1. 基本方法
根据贝叶斯公式,我们有 \[ P(Y|X)=\frac{P(Y) \cdot P(X|Y)}{P(X)} \] 其中,
2.1.1. \(P(X)\)
\(P(X)\) 是边缘概率,是一个作为归一化的证据(evidence)因子。
由于计算 \(P(X=x)\) 的计算不依赖于 \(Y\),即对于所有的 \(Y=c_k\) ,故该项是一个常数项,又由于后面会进行argmax运算,故该值的计算可以忽略
2.1.2. \(P(Y)\)
\(P(Y)\) 是先验概率,可以通过统计计算得到 \[ P(Y=c_k)=\frac{\sum_{i=1}^N I(y_i=c_k)}{N} \] \(I(y_i=c_k)\) 是一个二值函数,当 \(y_i=c_k\) 时,值为1;反之,值为0
为了避免0除错误,引入拉普拉斯平滑,原式变为 \[ P(Y=c_k)=\frac{\sum_{i=1}^N I(y_i=c_k) + \lambda}{N + K\lambda} \] 一般上,\(\lambda=1\)
2.1.3. \(P(X|Y)\)
\(P(X|Y)\) 是似然性概率,是朴素贝叶斯推断的重点,该值的通用计算公式为 \[ P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k),k=1,2,...,K \] 上式需要计算的参数是指数级,假设 \(x^{(j)},j=1,2,...,k\) 有 \(S_j\) 个可能取值,则需要计算的参数为 \(k\prod_j S_j\) 个。可以看出,计算量非常大,很难直接求出来。为了减少计算量,朴素贝叶斯作认为 \(X\) 的所有维度都是相互独立、完全正交的,即 \[ P(X=x|Y=c_k) = \prod_{j=1}^n P(X^{(j)}=x^{(j)}|Y=c_k) \] ### \(P(Y|X)\)
\(P(Y|X)\) 是后验概率,能使该值最大的 \(c_k\) ,便是分类器模型最终的输出值
于是,应用最大后验估计及独立性假设,分类器模型的函数简化为 \[ \begin{aligned} f(x) &= \arg \max _{c_k} P(Y=c_k|X=x) \\ &= \arg \max _{c_k} P(Y=c_k) \prod_{j} P(X^{(j)}=x^{(j)}|Y=c_k) \end{aligned} \]
2.2. 概率分布函数选择
好了,万事俱备,只差确定 \(P(X|Y)\) 的分布类型了。
一般根据输入数据的特征(离散型还是连续型)确定其服从的概率密度分布函数。
注:
离散型和连续型可以简单地理解为输入集合是否是确定的。
离散型数据,例如,人的年龄,数据的输入只能是一个整数,一定范围内的集合总数是确定的,实际多应用与文本中
连续性数据,例如,人的身高,数据的输入可以是任意值,一定范围内的集合总数是无限的
下面将不再给出各分布的一般形式,只给出其服从独立分布时的形式
2.2.1. 高斯判别
对于连续变量,一般可以认为其服从高斯分布,即 \[ X \sim N(\mu, \Sigma) \] 当 \(n=1\) 时, \[ P(X^{(j)}=x^{(j)}|\mu_j, \sigma_j^2,Y=c_k) = \frac{1}{\sqrt{2\pi}\sigma_j}\exp(-\frac{(x^{(j)}-\mu_j)^2}{2\sigma_j^2}) \] 当 \(x\) 的各个维度相互独立时, \[ P(X=x|\mu, \Sigma,Y=c_k) = \prod_{j=1}^n P(X^{(j)}=x^{(j)}|\mu_j, \sigma_j^2,Y=c_k) \]
注:
可令协方差矩阵为 \[ \Sigma = \begin{bmatrix} \sigma_{1}^2 &0 & \dots &0 \\ 0 & \ddots & & \vdots \\ \vdots & & \ddots & 0 \\ 0 & \cdots & 0 & \sigma_{n}^2 \end{bmatrix} _ {n \times n} = \text{diag}(\sigma_{1}^2, \cdots,\sigma_{n}^2) \] 则可以简化为 \[ P(X=x|\mu, \Sigma,Y=c_k) = \frac{1}{(2 \pi) ^ {n/2} |\Sigma| ^ {1/2}} \exp \left (-\frac{1}{2}(x-\mu) \right) ^ T \Sigma ^ {-1} (x-\mu) \]
模型效果如下
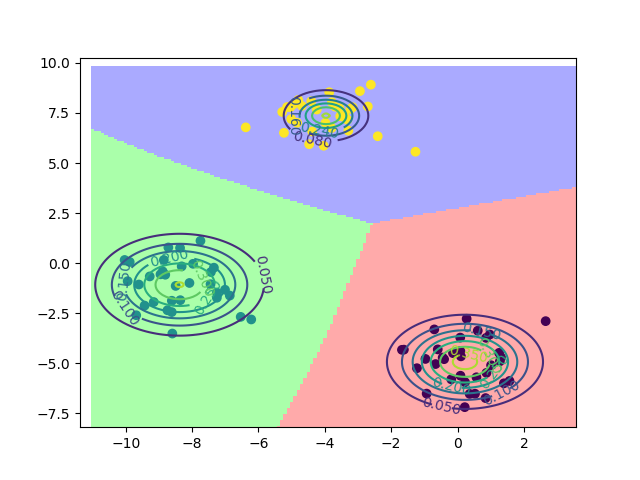
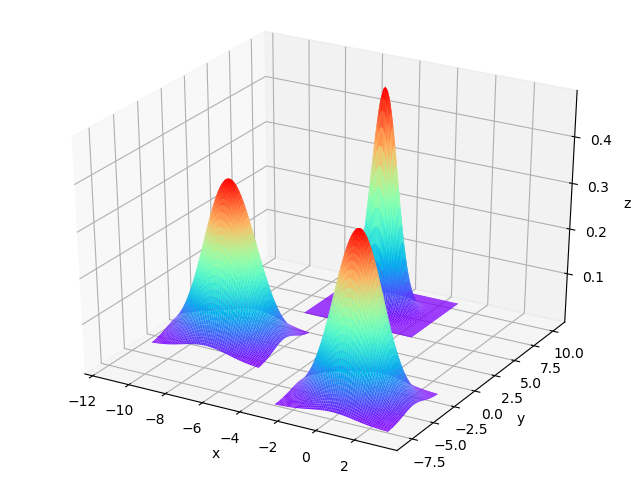
2.2.2. 多项式判别
对于离散型变量,一般可以认为其服从多项式分布,即 \[ X \sim \text{Mult}(n,p) \]
设 \(x^{(j)}\) 所有的可能取值数量的集合为 \(\{a_{j1},...,a_{jL} \}\),当\(n=1\) 时, \[ P(X^{(j)}=a_{j}|p_j,Y=c_k) = \frac{\sum_{i=1}^N I(x_{ij}=a_{jl},y_i=c_k)}{\sum_{i=1}^N I(y_i=c_k)} \]
注:
上面的表达式与常见的多项式分布的表达式并不相同,这是因为在朴素贝叶斯的多项式判别在应用多项式分布式时,对其做了一些简化:原来的多项式分布中预测的是某个类别出现多少次的概率,而多项式判别中预测的是某个类别出现一次的概率,所以实际上,多项式判别更为准确的叫法应该是Multinomial判别,但由于差别不大,所以一般都会把两者等同起来。
为了避免0除错误,一般会加入拉普拉斯平滑 \[ P(X^{(j)}=a_{jl}|p_j,Y=c_k) = \frac{\sum_{i=1}^N I(x_{ij}=a_{jl},y_i=c_k) + \lambda }{\sum_{i=1}^NI(y_i=c_k) + L \lambda} \]
当 \(x\) 的各个维度相互独立时,有 \[ P(X=a|n,p,Y=c_k) = \prod_{j=1}^n P(X^{(j)}=a_{j}|p_j,Y=c_k) \] > 注: > > 如果 \(x\) 的维度很高,进行累乘的时候容易精度丢失,所以一般对结果取log对数,即 > \[ > \log P(X=a|n,p,Y=c_k) = \sum_{j=1}^n \log P(X^{(j)}=a_{j}|p_j,Y=c_k) > \] > > > 累乘运算转化为累加运算,这也是likelihood函数常用的优化手段
2.2.3. 二项判别
二项判别同样针对的是离散型数据,即 \[ X \sim B(n,p) \] 当 \(n=1\) 时 \[ P(X^{(j)} =x^{(j)}|p_j,Y=c_k) = p_j^{x^{(j)}} (1-p_j)^{1-x^{(j)}} ,x^{(j)}\in \{0,1\} \] 其中, \[ p_j=\frac{\sum_{i=1}^N I(x_i=1,y_i=c_k)}{\sum_{i=1}^N I(y_i=c_k)} \]
注:
- 二项判别与多项式判别在概率计算上是完全一样的,两者区别在于统计粒度上。假设对于一个文本分类任务,\(x\) 是以单词作为特征量,以文档作为样本量的样本空间,则在多项式判别中,\(x_{ij}\) 表示 \(j\) 单词在 \(i\) 文档中出现了多少次;在二项判别中, \(x_{ij}\) 表示 \(j\) 单词在 \(i\) 文档中是否有出现过。
- 同样的,为了防止0除错误,加入拉普拉斯平滑
当 \(x\) 的各个维度相互独立时,有 \[ P(X=x|p,Y=c_k)=\prod_{j=1}^n P(X^{(j)}=x^{(j)}|p_j, Y=c_k) \] > 注: > > 同样的,为了避免向下溢出,采用对数似然函数 > \[ > \log P(X^{(j)} =x^{(j)}|Y=c_k) = \sum_{j=1}^n \left [ x^{(j)} \log p+(1-x^{(j)}) \log(1-p) \right ] > \] >
3. references
《统计学习方法》第4章,李航
《机器学习》第7章,周志华
See you~