线性回归(Linear Regression)是一种基于线性求解矩阵的回归算法
一般来说,很少有回归算法被单独提出来,因为回归算法一般都作为分类算法的中间产物而存在。这里单独作为一篇列出来,只要是因为线性回归太经典了,是作为后面提到的线性模型(包括SVM和神经网络)的基础,一般是作为机器学习入门的模型。(其实就是想水一篇笔记)
基于numpy的实现代码传送门
1. 输入输出
训练输入: \[ T=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中,
- \(x\) 为特征域,\(x_i \in \mathbb{R}^{n},i =1,2,...,N\)
- \(y\) 为标签域,\(y_i \in \mathbb{R}\)
测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^n \] 测试输出: \[ Y'=\{y'_1,\cdots,y'_{N'}\},y_i' \in \mathbb{R} \]
2. 模型效果
2.1. 训练效果
梯度下降法的训练效果
2.2. 最终效果
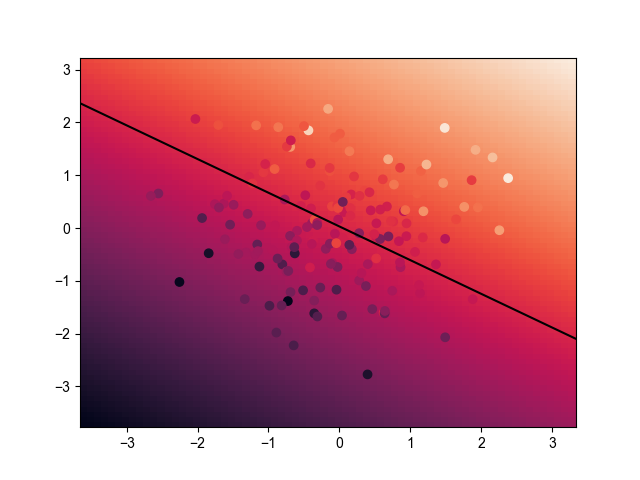
其中,展示的平面为 \(n=2\) 的特征域 \(S\) ;颜色越白,对应的标签值 \(y\) 越大,反之,则越小;黑色直线为特征域 \(S\) 的 \(y=0\) 的超平面
3. 模型推导
3.1. 基本方法
假设模型输入数据基本符合线性的分布,即 \(f(x) = w \cdot x + b\)
是不是感觉这条式子似曾相识,没错,这条函数式和感知机的模型函数式的相似,只不过感知机的 \(f(x)=0\) 以分割 \(-1\) 和 \(1\) 两个区域,线性回归并不需要分割平面,只需要拟合一个大概的值即可,即模型的函数为 \[ y' \approx f(x) = w \cdot x + b \]
线性回归是后面SVM和神经网络的雏形,特别是神经网络,就是由一个个线性模型像搭积木一样搭建起来。
3.2. 学习策略
问题转化为如何求未知变量 \(w\) 和 \(b\)
为了描述方便,令 \(W=[b,w_1,w_2,...,w_n]_{1 \times n}^T,X=[1,x^{(1)},x^{(2)},...,x^{(n)}]_{N\times n}\),使得 $ X W=w x + b$,
使用均方误差作为损失函数,即 \[ \begin{array}{ll} L(W) &= \frac{1}{N} \sum_{i=1}^m (f(x^{(i)}) - y^{(i)})^2 \\ &= \frac{1}{N} (XW-y)^T(XW-y) \\ &= \frac{1}{N} (W^TX^TXW-2W^TX^Ty+y^Ty) \end{array} \]
3.3. 学习算法
模型损失函数值最小时,模型的预测效果最好。因此,问题转化为求解损失函数的最小值
为此,可先求其偏导,即 \[ \frac{\partial L}{\partial W} = \frac{2X^T(XW-y)}{N} \] 当其偏导趋向于0时,模型的损失函数值最小。
使用以下两种方法,最终求得未知变量 \(W\)
3.3.1. 最小二乘法
当 \(X^TX\) 为满秩矩阵或者正定矩阵时,其偏导必有唯一最小值0,可直接令 \(\frac{\partial L}{\partial W} =0\),即可求解 \[ W=(X^TX)^{-1}X^Ty \]
满秩矩阵:对于方阵,满秩时,其行列式不为0。当 \(X\) 的特征数大于样例数时,\(X^TX\) 一定不满秩
3.3.2. 梯度下降法
但实际中,有些时候不满足上述条件,则可以使用万能逼近手段,求解凸函数的局部最优解,即求解 \[ W \leftarrow W - \alpha \frac{\partial L}{\partial W} \] 其中,\(\alpha\) 为学习率
不断迭代上式,直到达到最大迭代次数或损失函数的绝对值小于预设的阈值 \(\varepsilon\)
更新W的时候,如果每次更新都以 \(N'=N\) 全数据进行更新,极大可能会不收敛,所以一般取 \(N'=1\) 的单批次更新或者 \(N'=m\) 的 mini-batch 更新
4. references
《统计学习方法》第6章,李航
《机器学习》第3章,周志华
Add oil~