数据结构-匹配树

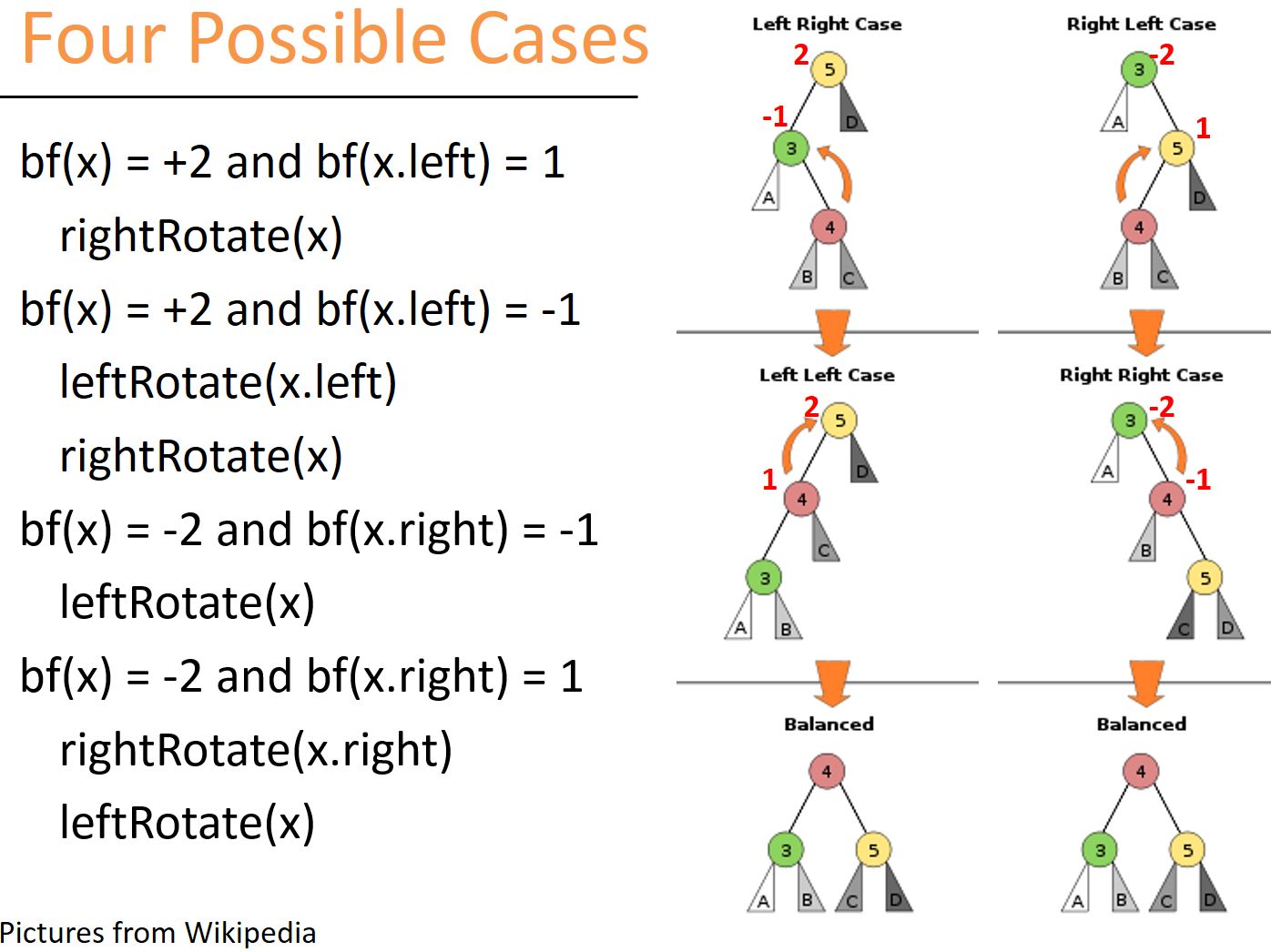
匹配树一般是为了优化短序列匹配问题的数据结构。

匹配问题一般输入一个长序列（匹配序列或主序列）以及一个短序列（模式序列）或其序列集合，输出匹配序列是否包含 模式序列 或其 序列集合的一部分。

特别地，匹配问题一般只用于字符串处理问题。

1. Trie树

实现代码传送门

1.1. 定义

Trie树（Retrieval Tree）又称前缀树或字典树。

• 特性

  • Trie树的每个节点具有3个内存空间——数据域、孩子指针域、终止标志域（为了后续查询方便，这个一般用来存放输出的内容）

  • 根节点不包含字符，除根节点以外每个节点只包含一个字符。

  • 从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。

  • 每个节点的所有子节点包含的字符串不相同。

• 优点

  可以最大限度地减少无谓的字符串比较，故可以用于词频统计和大量字符串排序。

• 缺点

  • 当序列集合相同的前缀很少时，树会变得很庞大，浪费很多内存空间。

  • 如果数据存储在外部存储器等较慢位置，Trie会较hash速度慢（hash访问\(O(1)\)次外存，Trie访问\(O(\text{树高})\) 次外存）。

  • 长的浮点数等会让链变得很长。

• 应用场合

  • 判断某个元素是否在一个元素集合中，这时候退化为一棵搜索树
  • 匹配所有以某个序列为前缀的序列集合，例如，搜索框和输入法智能联想功能
  • 给定模式串，输入主串进行匹配，类似Python的 re.match 的模式匹配
  • 也可以用来做分词，具体参考这篇Trie树分词

1.2. 构建/插入

输入

模式序列集合

流程

由于输的构建就是将输入集合中的序列一个一个地插入，故下面只介绍一个序列插入的流程

1. 把根节点作为当前节点，同时对于输入字符串序列 A，把第一位字符作为当前字符。
2. 遍历当前节点的所有子节点，匹配数据域与当前字符相同的节点。如果匹配成功，则将匹配成功的节点作为当前节点；否则，创建一个数据域为该字符的节点（终止标志符默认为假），并让当前节点指向该节点，然后将该节点作为当前节点。
3. 把下一位字符当做当前字符。
4. 重复步骤2~3，直到没有下一位字符。把当前节点的终止标志符设为真。

例子

输入序列集合为

['the', 'they', 'them', 'their', 'theirs', 'themselves', 'he', 'hey', 'se', 'self', 'their']

得到的Trie树为

None(0)-->t(0)-->h(0)-->e(1)-->y(1)
                           └-->m(1)-->s(0)-->e(0)-->l(0)-->v(0)-->e(0)-->s(1)
                           └-->i(0)-->r(1)-->s(1)
      └-->h(0)-->e(1)-->y(1)
      └-->s(0)-->e(1)-->l(0)-->f(1)

1.3. 查找

流程

查找和插入的流程是差不多的，只需要将插入的：

• 步骤2中的失配操作换成直接退出并返回假；
• 步骤4中的“把当前节点的终止标志符设为真”换成返回当前节点的终止标志符。

替换后的流程即为查找的流程。

例子

查找 they 的结果为真，查找 thea 的结果为假。

1.4. 删除

流程

1. 从根节点开始查找输入序列，如果中间有字符失配，则直接返回退出，删除失败。否则，将匹配到的最后节点作为当前节点，并将其终止标志符置为假。
2. 如果当前节点是叶子节点且终止标志符为假，则删除当前节点，并递归地将其父节点作为当前节点；否则，则返回退出，删除成功；
3. 递归重复步骤2.

例子

删除 they 后的Trie树为

None(0)-->t(0)-->h(0)-->e(1)-->m(1)-->s(0)-->e(0)-->l(0)-->v(0)-->e(0)-->s(1)
                           └-->i(0)-->r(1)-->s(1)
      └-->h(0)-->e(1)-->y(1)
      └-->s(0)-->e(1)-->l(0)-->f(1)

2. AC自动机

实现代码传送门

2.1. 定义

AC自动机（Aho-Corasick automaton）是一种基于Trie树和KMP算法的后缀树。

• 特性

  • Trie树的每个节点具有4个内存空间——数据域、孩子指针域、输出数据域（可以看做Trie树的终止标志域）、fail指针
  • 字符串匹配的时候，当前字符匹配成功时，流程和Trie树一样；当出现失配情况时，AC自动机可以通过fail指针跳到其他的分支上，重新进行匹配（可以理解为一个误入歧途的人通过正确的指引重新走上光明的大道）

• 优点

  不同于Trie树只能匹配输入序列开始的位置，AC自动机可以匹配输入序列任意的位置

• 缺点

  创建的时候需要花费大量的时间，并且树一旦被创建就不能做增删改操作。

• 应用场合

  多用于正则匹配，类似Python的 re.search

下面以中序线索树作为例子。

2.2. 构建

输入

模式序列集合

流程

1. 构建一棵Trie树（Trie树的终止标志域一定得存输出内容）。
2. 添加fail指针。建构过程要求父亲节点的fail指针已经建好，而且一层层都要建好，所以采用bfs实现fail指针的添加。首先先把根节点的fail指针指向自己。然后按层从树的第二层开始遍历每一个节点（注意遍历的时候需要保存当前节点及其父节点），按步骤3为每个节点添加fail指针。
3. 设当前节点为 p，其值为 c，父节点为 f，顺着 f.fail 查询其子节点，如果存在值为 c 的子节点，则将 p.fail 指向该子节点；反之，则另 f=f.fail，重复步骤3，直到f.fail指针指向自己（也就是根节点了）为止，那么，就将 p.fail 指向根节点。

例子

输入序列集合为

['the', 'they', 'them', 'their', 'theirs', 'themselves', 'he', 'hey', 'se', 'self', 'their']

得到的AC自动机如下（fail指针没有表示出来）

None(0)-->t(0)-->h(0)-->e(1)-->y(1)
                           └-->m(1)-->s(0)-->e(0)-->l(0)-->v(0)-->e(0)-->s(1)
                           └-->i(0)-->r(1)-->s(1)
      └-->h(0)-->e(1)-->y(1)
      └-->s(0)-->e(1)-->l(0)-->f(1)

2.3. 匹配

输入

一个长序列

流程

1. 按以下步骤从左往右遍历输入序列的每一个元素。
2. 设当前元素的值为 c，当前节点为 p。
3. 遍历 p 的子节点。
4. 如果存在子节点的值和 c 一样，则匹配成功，则查询该节点以及该节点的fail指针指向的节点是否有输出，如果有则保存其输出，反之，则将该节点作为当前节点，继续遍历下一个元素。
5. 如果不存在，如果 p 为根节点，则直接遍历下一个元素，否则，令 p=p.fail，重复步骤3~5

一些解释

为什么称AC自动机为后缀树呢，以一棵只有 they 、 hey 和 say 三个分支的AC自动机为例，明显的，hey 作为 they 的后缀，hey 会通过fail指针连接到 they 上。当我们匹配到 y 的时候，按照Trie树只会输出 they，但到了AC自动机，还会沿着fail指针，访问隔壁 hey 分支的 y 节点，不会访问 say 分支的 y 节点，这时就会输出 hey （相同的灵魂之间是相通，但你我的外在却是不一样的，而不一样的灵魂，我一点都不关心），所以，这是后缀的。

例子

输入长集合为 thuthemselveselftheirthey，输出（输出序列-开始下标）为

('the', 3), 
('he', 4), 
('them', 3), 
('se', 7), 
('themselves', 3), 
('se', 12), 
('self', 12), 
('the', 16), 
('he', 17), 
('their', 16), 
('the', 21), 
('he', 22), 
('they', 21), 
('hey', 22)

---

Have fun~