运算树一般是为了优化某种区间运算的树。
1. 线索树
实现代码传送门
1.1. 定义
线索树(Thread Tree)是专门为了优化遍历而设计出来的二叉树。
特性
线索树的每个节点具有5个内存空间——数据域、前驱指针(左指针)、后继指针(右指针)、ltag、rtag
其中,前驱和后继是相对于遍历序列来说的。例如,对于中序序列
abcdef,b是c的前驱,d是c的后继。种类
如果是对中序遍历进行优化的则叫中序线索树,除此以外,还有后序线索树和前序线索树,但后面两者用得比较少。
优点
这种二叉树的精妙之处在于把递归的遍历转换成循环的遍历。
线索树从某一节点出发查询其前驱和后继的时间复杂度都是 \(O(1)\),而普通二叉树从某一节点出发查询其前驱和后继的时间复杂度最好的情况是 \(O(1)\),最坏的情况是 \(O(n)\)。
缺点
一棵树只能优化一种遍历,如果想要优化其他遍历,需要重新建树。
应用场合
适用于频繁查询某节点的前驱和后续的场合。
下面以中序线索树作为例子。
1.2. 构建
输入
树的顺序表数组
流程
- 对于输入数据,按照构建普通二叉树的方法构建一棵二叉树。默认把所有节点的ltag和rtag置为0
- 中序遍历二叉树,分别保存当前节点以及上一个访问过的节点,即前驱节点。
- 遍历开始时,把中序遍历序列的第一个元素,即最左下角的元素,将其ltag置1,左指针可以指向根节点或者一个自定义的哨兵节点(该节点的左指针指向根节点),这个只会影响遍历开始的判断条件。然后继续下面的操作。
- 如果当前节点没有左指针时,把当前节点的ltag置1,且把左指针指向前驱节点。
- 如果前驱节点没有右指针,把前驱节点的rtag置1,且把前驱节点的右指针指向当前节点。
- 遍历结束后,把中序遍历中最后一个节点的rtag置1,且把后继指针指向根节点或哨兵节点。
1.3. 遍历
基于带哨兵节点的中序线索树的中序遍历流程如下:
- 把头节点作为当前节点,开始遍历。
- 从当前节点出发,沿左指针往下走,直到遇到 ltag 为1的节点,记录当前节点。
- 沿当前节点的后继指针,直到 rtag 为0或当前节点的右孩子不是头节点,记录遍历过的节点。
- 把当前节点的右孩子作为当前节点,重复步骤2~3,直到当前节点为头节点。
2. 线段树
实现代码传送门
2.1. 定义
线段树(Segment Tree)是专门为了优化区间查询而设计出来的完全二叉树。
特性
线段树的把输入数据作为叶子节点,每个主节点存储其所有叶子节点运算的结果。线段树的构造、更新、查询的根本思想在于二分法。
优点
可以很快地查询出一个区间的运算结果。
节点更新和区间查询的时间复杂度都为 \(O(\log n)\)
缺点
线段树的空间代价很高,对于输入数量为 \(n\) 的数组,最坏情况需要 \(4n\) 个节点。
线段树一旦建立,只能修改某一节点的值,不能增加或删除节点。
应用场合
适用于运算频繁但数据量不大且不频繁改动的场合。
种类
如果是对叶子节点进行求和则为求和线段树,除此以外还有累乘线段树,最大/最小值线段树等。
下面以求和线段树作为例子。
2.2. 构建
输入
任意数组序列
流程
- 对于一个输入长度为 \(n\) 的数组,分成 \([0, \lfloor n/2 \rfloor )\) 和 \([\lfloor n/2 \rfloor, n)\) 左右两部分
- 把分出来的左右两部分,分别递归地作为输入数组,重复执行步骤1,直到分出来的区间中只有一个元素。然后,递归返回一个值为该元素的叶子节点。
- 后序遍历操作,递归地返回所有地非叶子节点。每个非叶子节点的值等于返回的左右节点值之和。
例子
输入数组为 [0, 1, 2, 3, 4, 5, 6, 7, 8, 9],构建的线索树如下:
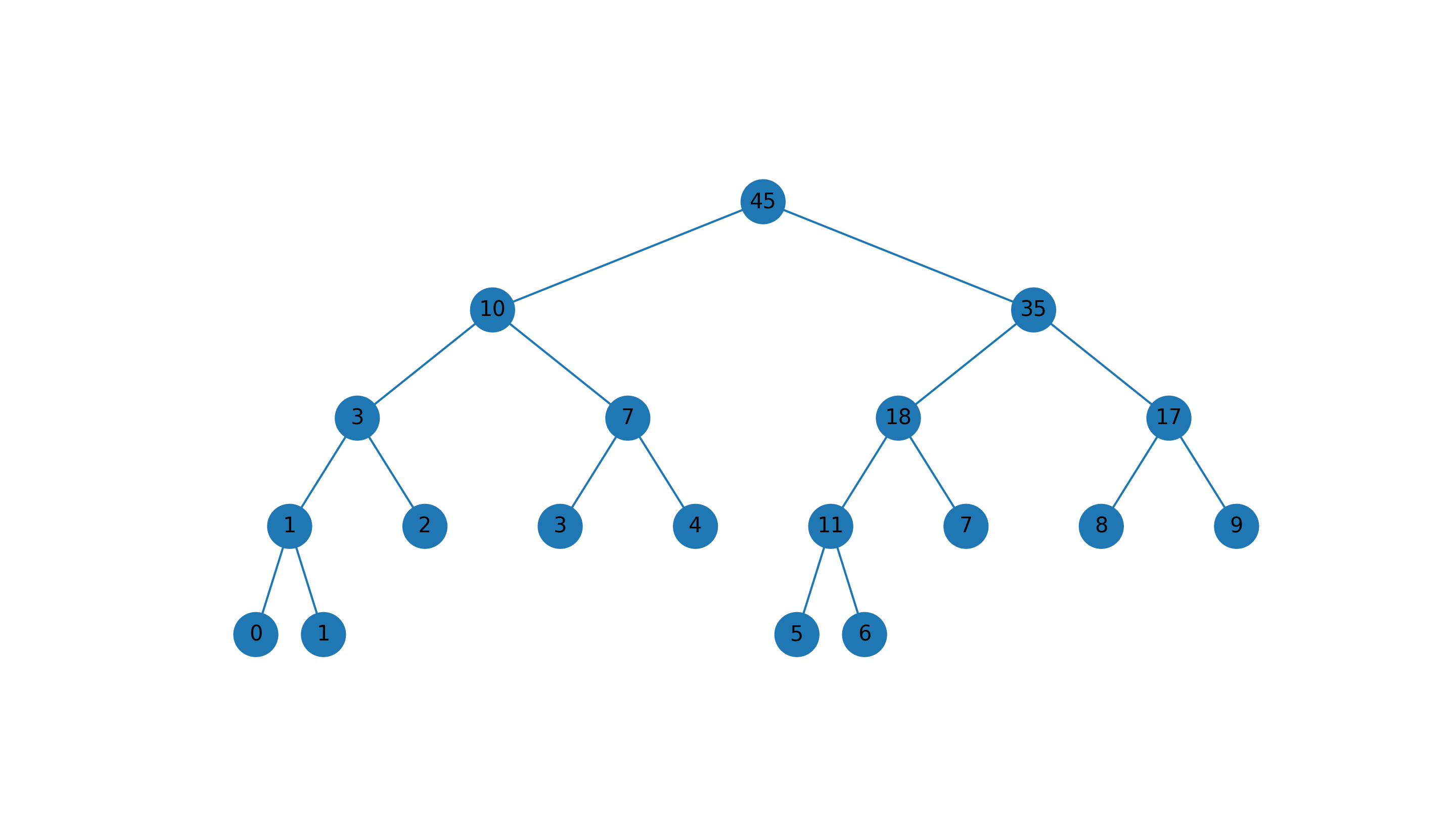
2.3. 更新
- 二分查找对应的节点,然后把该节点的值更改
- 递归地从下往上,更改该节点的所有祖先节点,每个节点的值为当前子节点值之和。
2.4. 查询
流程
- 从根节点出发进行遍历。
- 比较当前节点存储输入数组的运算结果的区间(设为 \(A_1\) )和查询的区间(设为 \(A_2\) )。
- 如果 \(A_1 \not \subset A_2\),则跳过该节点。
- 如果 \(A_1 \subset A_2\),则返回当前节点。
- 否则继续往下遍历。
- 把所有返回的节点进行求和运算,得到查询结果。
例子
上面构造的线段树,区间 \([2, 5]\) 的查询结果为 \(2+7+5=14\)
3. 索引树
实现代码传送门
3.1. 定义
索引树(Binary Indexed Tree)又称 Fenwick 树,也是专门为了优化区间求和而设计出来的二叉树。
特性
索引树只用到顺序表存储,不用链式存储(其实严格意义上来说,这不算是一棵二叉树)。
索引树需要定义一个函数 \(lowbit(i) = i \& (-i)\) ,实质表现为,对于一个正整数\(i\),\(lowbit(i)\)为\(i\)的二进制表达式中最右边的1所对应的值,正如函数的名字一样(纳尼?低位?low b?黑人问号?),取低位的数值。例如,对于十进制数 \(14_{(10)}\),其二进制形式为 \(1110_{(2)}\),\(lowbit(14) = 10_{(2)}=2_{(10)}\)
索引树中,任一节点 \(C_i\) 的高度为 \(lowbit(i)\) ,父节点为 \(C_{i + lowbit(i)}\),例如,\(C_{14}\) 的高度为2,父节点为 \(C_{16}\)
优点
更新任一节点和查询任一区间求和的时间复杂度为 \(O(\log n)\),创建索引树的时间复杂度为 \(O(n \log n)\)
空间复杂度上,需要 \(2^{\lceil \log_2 n \rceil } + 1\) 个节点,即最好情况需要 \(n + 1\) 个节点,最坏情况需要 \(2n - 1\) 个节点,比线段树要少得多。(省掉的线段树的右节点部分,大概减少了一半的内存空间)
缺点
只能用于区间求和,不能用作其他运算。
应用场合
需要区间求和的场合。
3.2. 构建/更新
输入
任意数组序列
流程
- 对于输入长度为n的数组序列\(A\),创建一个大小为 \(2^{\lceil \log_2 n \rceil } + 1\) 的顺序表\(C\)。顺序表内元素都初始化为0,为了方便计算,输入数组和顺序表的下标都从1开始(即顺序表中下标为0的元素只起到占位的作用)。
- 循环遍历输入序列,逐个更新顺序表中的元素。
- 对于输入数组中下标为 \(i\) 的元素,顺序表中开始更新的节点位置为 \(i+1\) 。然后对当前节点及其所有的祖先节点(即不断的往右遍历 \(C_{i + lowbit(i)}\))的值都加上输入元素的值。
- 输入序列遍历结束后,索引树构建完毕。
生成的索引树的结构如下(下图中,\(A\) 从下标为1开始,只需将其下标往左挪一位,便与上述步骤中的 \(A\) 的下标一致了):
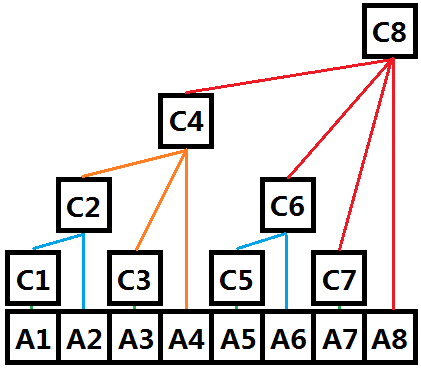
例子
输入数组为 [0, 1, 2, 3, 4, 5, 6, 7, 8, 9],构建的索引树的顺序表为:C=[0, 0, 1, 2, 6, 4, 9, 6, 28, 8, 17, 0, 17, 0, 0, 0, 45]
3.3. 查询
首先,我们先来分析下索引树查询的原理。
对于任意非负整数 \(x\),都可以分解为多个二次幂之和,即 \[ x = \sum_{k=0}^{\lfloor \log_2 x \rfloor} a_k 2^k \]
其中,\(a_k\) 为对应二进制位上的值,例如,\(14_{10}=1110_{2}=1000_{2}+100_{2}+10_{2}=8_{10}+4_{10}+2_{10}\),
又从上面节点更新的流程可以得出,对于任一节点 \(C_{i+1}\) ,其值等于区间 \((i-lowbit(i), i]\) 之和,即
\[ C_{i+1} = \sum_{k=0}^{lowbit(i)-1} a_k A_{i-k} \]
所以,对于查询区间 \((0,x]\) 之和,我们得到查询函数 \[ q([0,x])=q((0, 2^{\lfloor \log_2 x \rfloor }]) + \sum_{k=0}^{\lfloor \log_2 x \rfloor - 1}q((\sum_{j=k+1}^{\lfloor \log_2 x \rfloor} a_j 2^j, \sum_{j=k}^{\lfloor \log_2 x \rfloor} a_j 2^j]) \] 例如,\(q((0,14])=q((0,8]) + q((8,12]) + q((12, 14])\)
为什么要这样分解,因为我们可以注意到, \[ \sum_{j=k+1}^{\lfloor \log_2 x \rfloor} 2^k = \sum_{j=k}^{\lfloor \log_2 x \rfloor} 2^k - lowbit(\sum_{j=k}^{\lfloor \log_2 x \rfloor} 2^k) \] 故
\[ \begin{array}{ll} q((0,14]) &= q((8-lowbit(8), 8])+q((12-lowbit(12),12])+q((14-lowbit(14),14]) \\ &=C_9+C_{13}+C_{15} \end{array} \]
所以,我们得到查询区间 \([0,x]\) 求和公式 \[ q((0,x])=\sum_{k=0}^{\lfloor \log_2 x \rfloor } a_k C_{ 1 + \sum_{j=k}^{\lfloor \log_2 x \rfloor} 2^j} \] 所以,查询区间 $ (0,x]$ 求和流程简化如下:
- 初始化求和结果
s=0 s += C[x+1]x -= lowbit(x)- 循环步骤2~3,直到
x=0,返回求和结果s
而对于查询区间 \([l, r]\),由于这是前缀和查询,其查询结果为 \(q((0,r])-q((0,l-1])\)
例子
上面构造的索引树,区间 \([2, 5]\) 的查询结果为 \(C_6+C_4-C_2=9+6-1=14\)
4. 哈夫曼树
实现代码传送门
4.1. 定义
哈夫曼树(Huffman Tree)是专门为了优化带权路径运算设计出来的二叉树。
特性
每个哈夫曼树节点包含4份内存空间——数据域、父节点到当前节点的路径长度/权值、左指针、右指针。
优点
应用场合
通信领域应用广泛。
4.2. 构建
输入
节点数据-路径权值(key-value) 的字典表
流程
- 为每个输入创建一棵以key-value值作为根节点的树,形成一个森林F。
- 从F中抽出两个根节点的权值最小的树,创建一棵只有一个根节点的树,把这两棵树作为其左右子树,其根节点的权值为左右节点的权值之和。把新创建的树加入F中。
- 重复步骤2,直到F中只包含一棵树,这棵树就是创建的哈夫曼树。
例子
输入字典 {'a': 4, 'b': 2, 'c': 6, 'd': 8, 'e': 3, 'f': 2}, 构建的哈夫曼树如下:
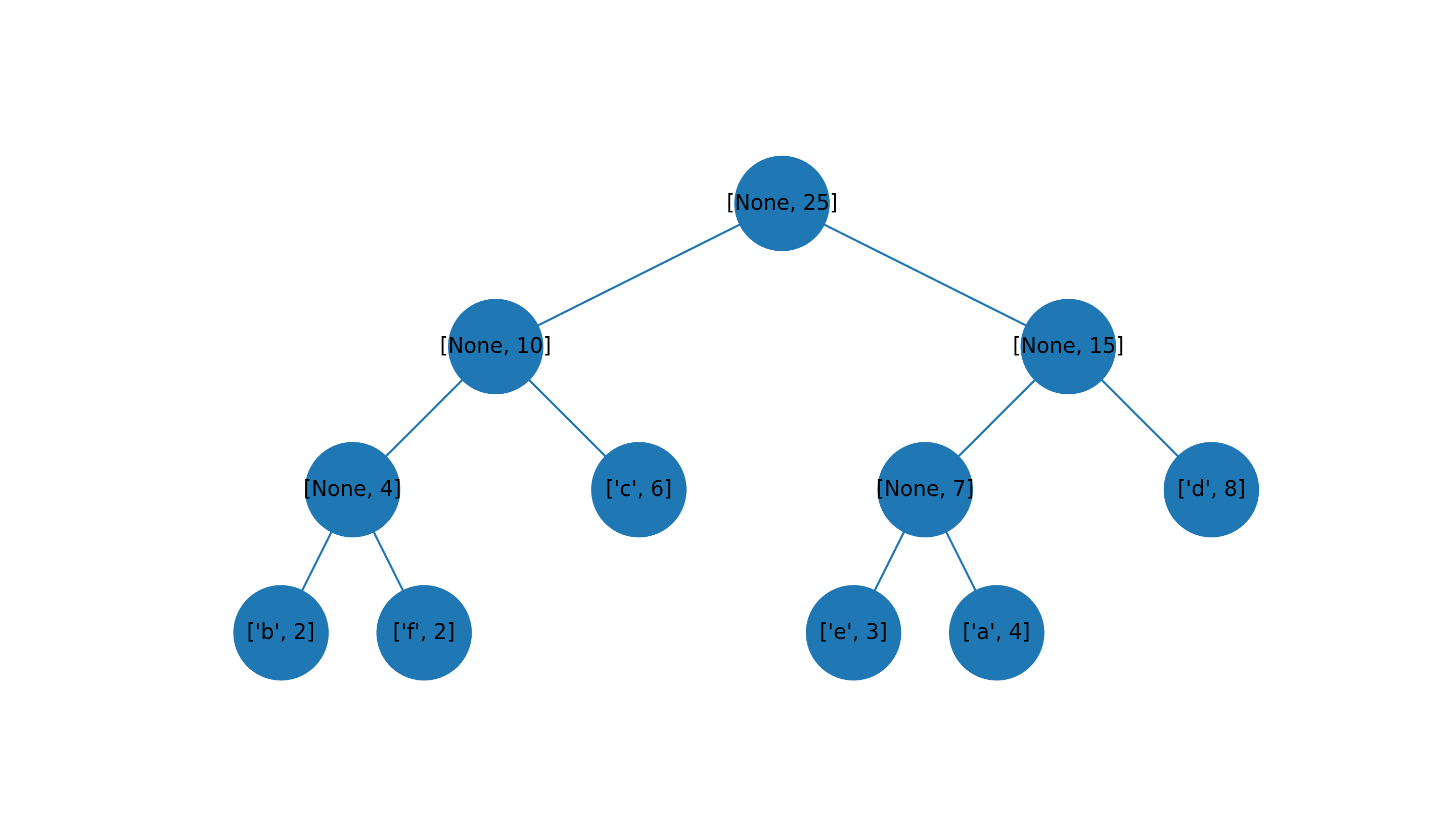
4.3. 带权路径长度计算
带权路径长度的计算公式如下: \[ WPL=\sum_{k=1}^n w_k l_k \] 其中 \(w_k\) 为叶子节点的权值,\(l_k\) 为当前深度减1。
例如,上面例子中,带权路径长度WPL为61
哈夫曼树首先选择权值较小的,保证权值较大的离根较近,这样计算带权路径长度时,就会得到最小的带权路径长度,所以其核心思想是贪心算法。
4.4. 哈夫曼编码
哈夫曼编码就是根节点到每个叶子节点的路径编码。
深度优先遍历,如果经过左节点则为0,如果经过右节点则为1.
例如,上面例子中,哈夫曼编码为 {'b': '000', 'f': '001', 'c': '01', 'e': '100', 'a': '101', 'd': '11'}
哈夫曼编码为不等长编码。不等长编码要满足任何一个字符编码都不能是其他任意一个字符编码的前缀的条件,满足这一条件的编码称为前缀编码。
对于上面只有6个元素的等长编码,需要使用一个3位二进制进行编码,总体编码长度为75位二进制,而哈夫曼编码后,总体的编码长度为61位二进制,总体编码大小降低了。
当然,这里涉及到信息熵等知识,这里只是简单地介绍,后面会有专门的章节进行记录。
Farewell~

