1. 输入输出

Input:

样本空间 \[ X= \{x_1, x_2, ..., x_N\},x_i \in \mathbb{R}^n \] 需要划分的类簇个数 $k$

Output:

样本空间中每个点的预测类别 \[ Y=\{y_1,y_2,...,y_{N}\},y_i \in \{0,1,...,k\} \] 类簇集合 \[ C=\{C_1,C_2,...C_k\},C_i=\{x \in X | y = y_i \} \]

2. 模型效果

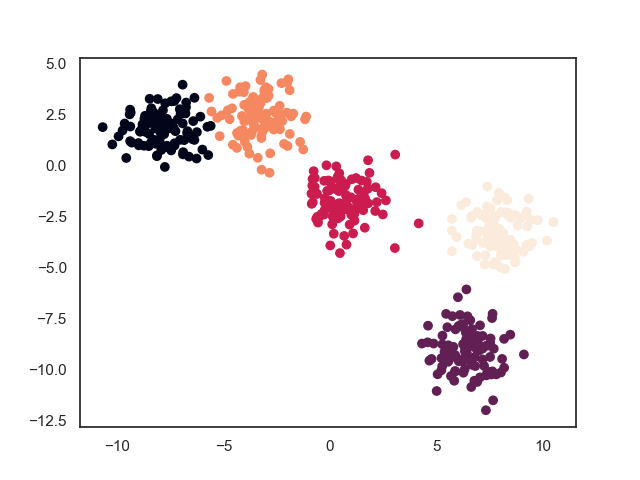
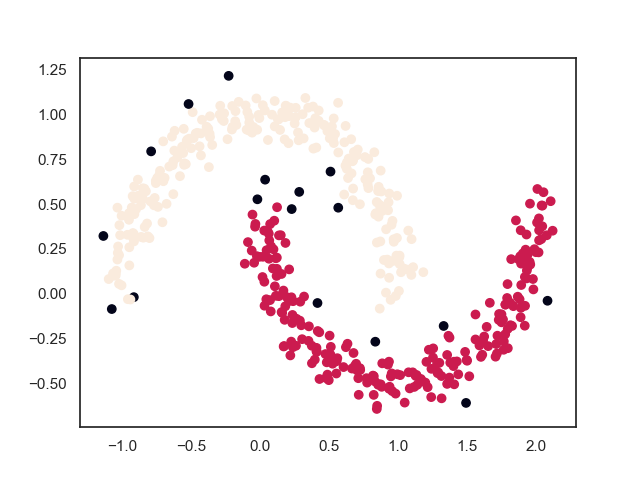
2.1. 训练效果

上图中，中间的样本为真实样本情况，外围的样本为映射到单位圆上的情况。

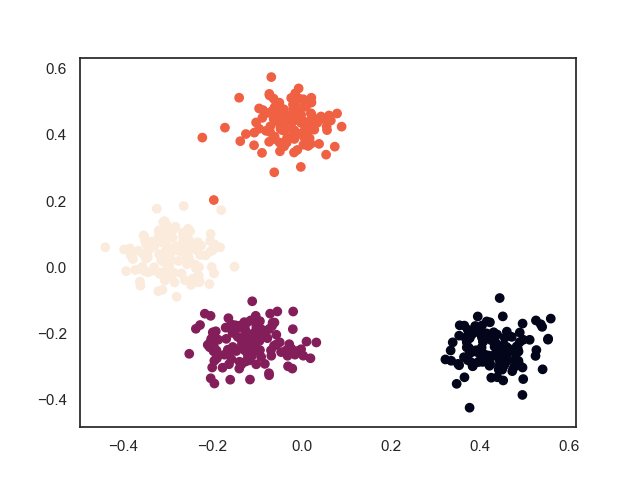
2.2. 最终结果

3. 模型推导

3.1. 基本方法

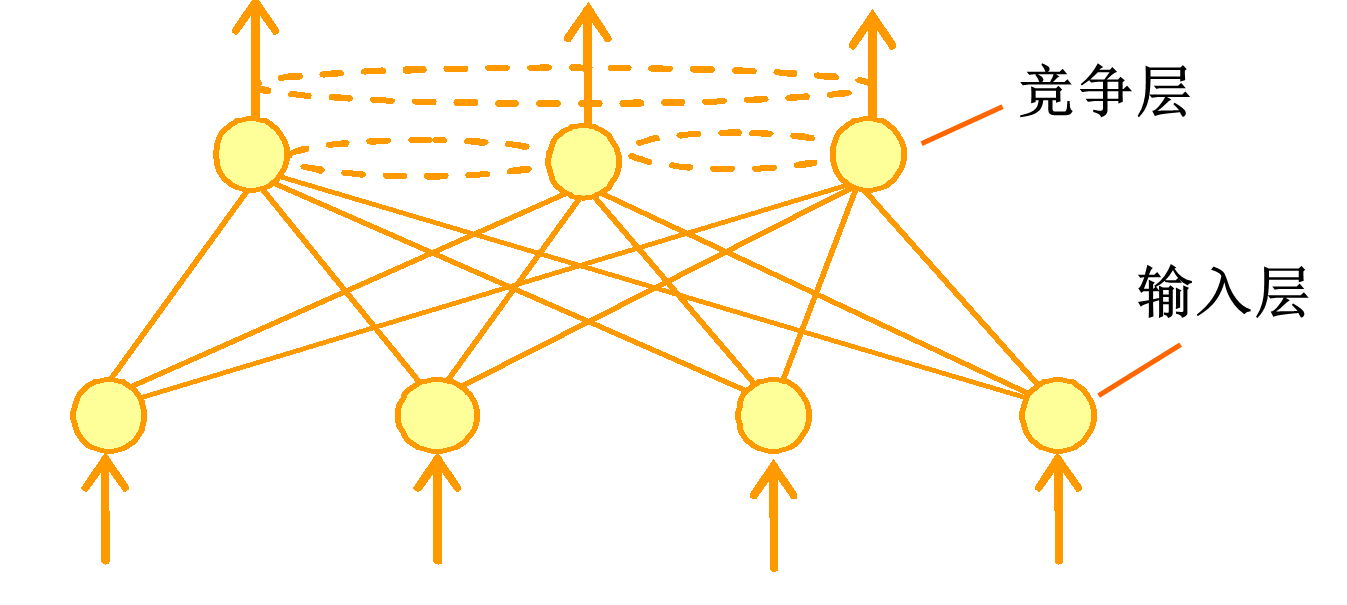
SOM模型只包含一层输入层和一层竞争层，如下所示

设输入层的参数为 $X=[x_1,...,x_N]_{N\times n}$，其中每个神经元的权值为 $x \in R^{1\times n}$ ，竞争层的参数为 $W = [w_1, ...,w_k]_{k \times n}$，其中每个神经元的权值为 $w \in R^{1 \times n}$

SOM算法几何意思是，取值向量不断向样本向量方向靠近，所以理论上，模型最终会使得每一个竞争层的神经元都归属于一个簇。

故只要计算 $x$ 与各个 $w$ 的相似度，求得胜者神经元，即可得到 $x$ 对应的类别。

相似度计算采用余弦相似度，可得模型函数为 \[ f(x) = \arg\max_j \{ \frac{x}{\|x\|_2} \cdot (\frac{w_j}{\|w_j\|_2})^T\} \]

3.2. 学习策略

SOM算法采取竞争学习策略，竞争层的每个神经元之间相互竞争，争夺权值更新的权利，即所谓的胜者为王（Winner take all）思想。更加具体地，对于当前输入样本 $x$，只有与其最相似的神经元才会得到更新。

按照其基本思想，每次只更新一个神经元，Kohonen教授对其进行了改进，提出了SOM网。对于获胜神经元，应当对附近的神经元也应该造成一定的影响，这种影响应该是由远及近，随时间由大到小的。更加具体的，以获胜神经元为中心，划出一个半径为 $R$ 的邻域 $N(w)$，落在邻域内的权值得到一个随距离远近而改变的权值更新。

这里提供一个可供选择的邻域半径 $R$ 更新函数 $R = k(1- \frac{t}{t_m})$，其中 $t$ 为当前迭代次数，$t_m$ 为最大迭代次数。

SOM网可以提高学习效率，而且一定程度上缓解“死节点”（一些神经元从未获胜造成权值一直没有被更新）的问题，但这种更新方式会使距离较近的权值重叠在一起，表现为两个簇合并成一个簇，虽然一定程度上起到到自适应选择类簇的作用，但如果你确信样本空间应该被分为 $k$ 类，这造成一定的副作用。所以SOM网更新策略是非必须的，可以自行斟酌选择是否采用该策略。

另外，所谓的自组织映射，即自适应地改变网络参数与结构，还包括学习率的自适应更新。这应该一个随迭代次数 $t$ 增加、以及距离获胜神经元的距离 $r$ 增大而减小的变量。这里提供一个可供选择的更新函数 $\eta \leftarrow \eta e^{-r}$

3.3. 学习算法

Init:

初始化竞争层的权值，一种的简单的方法是随机选取 $k$ 个输入样本作为权值，即 $w_j = x_{random}$
初始学习率 $\eta_0$
计算单位样本向量 $\hat{x} = \frac{x}{\|x\|_2}$

Repeat:

计算单位神经元向量 $\hat{w_j} = \frac{w_j}{\|w_j\|_2}$
求获胜神经元，$j = \arg\max_j \{ \hat{x} \cdot \hat{w_j}^T\}$
计算获胜神经元的邻域半径 $ R = k(1- )$，并求取落在邻域半径内的其他神经元 $x_i \in N(w_j)$ ，并计算其与获胜神经元的距离 $r_i = \|w_i - w_j \|_2$
更新学习率，$\eta_i = \frac{\eta_0 e^{-r_i}}{1 + t}$
更新权值，$w_i = \hat{w_i} + \eta_i(\hat{x_i} - \hat{w_i})$

Until: $\eta < \delta$ 或达到最大迭代次数