个人基于pytorch的实现代码
目标检测任务其实就是分类任务（目标类别）+回归任务（目标位置坐标四元组），也可以简单地看做是分类任务的一种特殊情况。因此，该类任务的指标也可以看作是多个基础指标的综合体。
1. 0级指标
普通分类任务判断预测是否正确，可以直接通过比较类别的值即可。但目标检测任务由于还需要比较位置，所以还需要一些专门的计算指标来判断预测的正确性。实际上，比较两个目标是否重合，可以看作是聚类任务中两个簇的相关性，所以是可以直接套用聚类的一些方法进行计算。
由于该级指标的计算在分类任务的1级指标之前，所以我姑且把计算预测是否正确的指标定义为0级指标
1.1. IOU
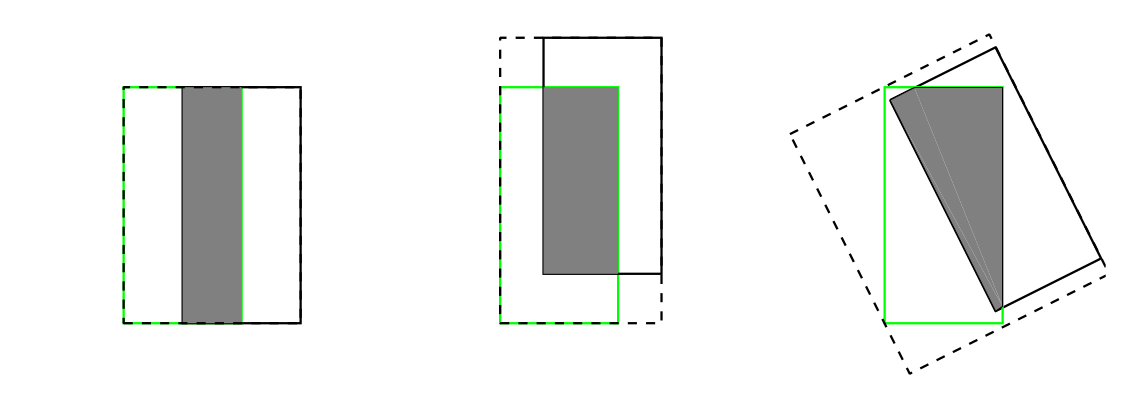
交并比（Intersection Over Union，IOU），反应两个目标的交集与并集之比。
\[
IOU = \frac{A \cap B}{A \cup B}
\]
注：IOU其实就是Jaccard系数的一种特殊情况，Jaccard系数在笔记数学工具-常用聚类任务评估指标已经提及过了
一些不足：
两者不重叠时，iou恒为0，不能反映两者距离的远近
无法从iou的值得出两者重叠的情况，如下所示，重叠面积一样，但无法重叠情况不一样
当一个大目标完全包含一个小目标时，尽管是完全重叠，但IOU却可能很小
1.2. GIOU
相关论文：Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression
\[
GIOU = IOU-\frac{C-(A \cup B)}{C}
\] 其中，
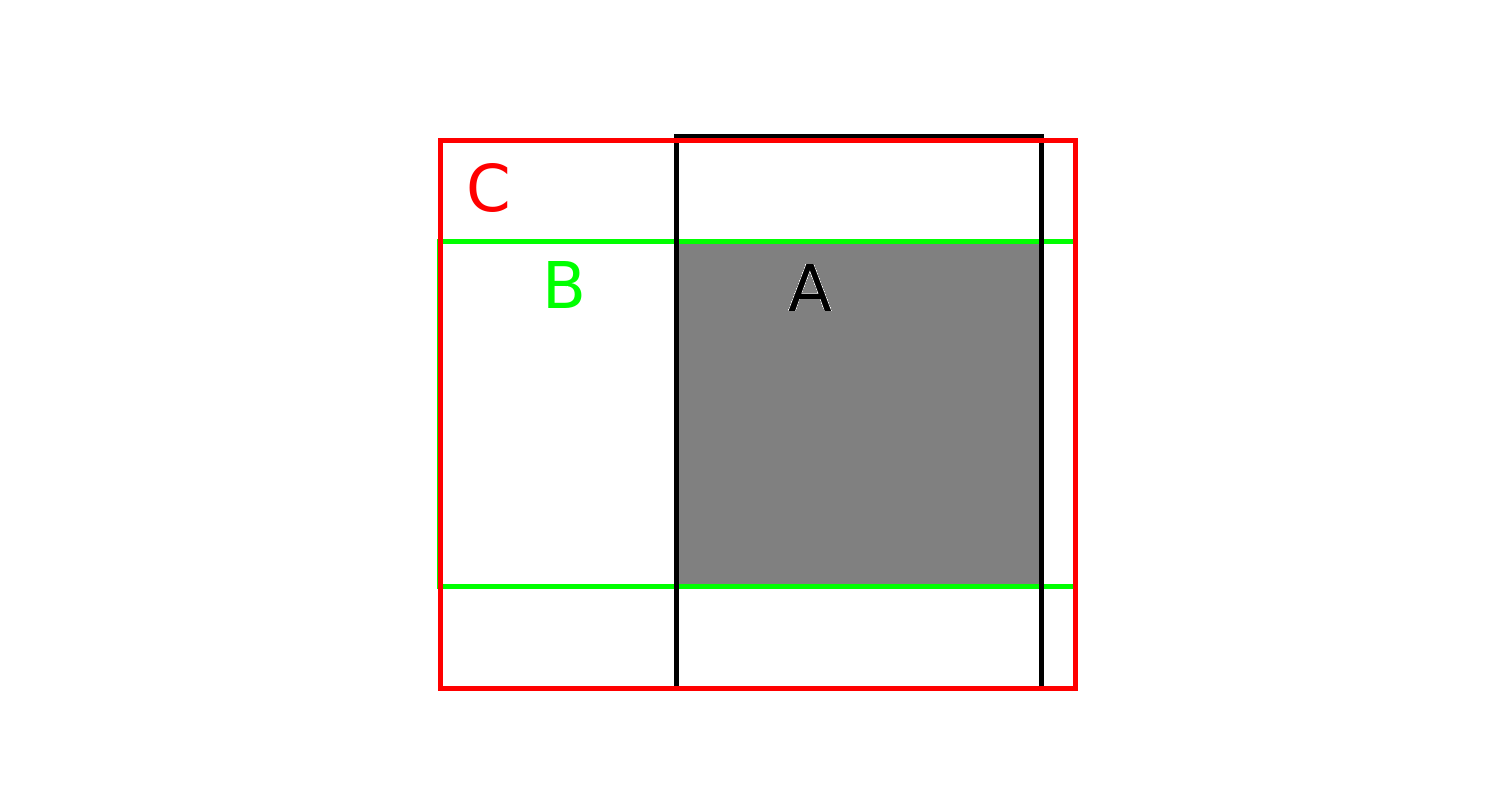
C是A和B的外接框，\(C-(A \cup B)\) 是C与A和B并集的差集
一些不足：
- 当一个大目标完全包含一个小目标时，GIOU退化为IOU
1.3. DIOU
相关论文：Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression
\[
DIOU = IOU - \frac{d^2}{c^2}
\] 其中，
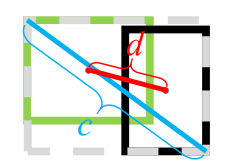
d是两个目标中心点的距离，c是外界框对角线的长度
一些不足：
- 即使在中心点、外接框、重叠面积不变的情况下，目标框的长宽比依然可以有多种不同的情况
1.4. CIOU
相关论文：Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression
Complete IoU，是DIOU的补充，对目标框的长宽比也加以控制
\[ CIOU = IOU - \frac{d^2}{c^2} - \alpha v \] 其中，
\(\alpha\) 是权重系数，一般设为 \(\alpha=\frac{v}{(1-IOU)+v}\)
\(v\) 是宽高比的相似性，一般设为 \(v=\frac{4}{\pi^{2}}\left(\arctan \frac{w^{g}}{h^{g}}-\arctan \frac{w^p}{h^p}\right)^{2}\)，其中，\(w, h\) 分别为输入图片的宽和高
2. 三级指标
2.1. P-R曲线
目标检测的P-R曲线和一般的分类任务中的定义不太一样。
一般的分类任务中，会选取不同的分类阈值，重新划分正负样本集合，然后计算出一个PR集合，最后作出PR曲线。
目标检测中，IOU给定后，正负样本就已经确定了。我们不会选择选取多个IOU值，重新划分正负样本的方式来计算PR曲线（后面还会有相应的指标表示不同IOU值的PR曲线）。我们会先按置信度对预测结果进行排序，然后逐样本如下计算一次PR值 \[ R = \frac{|TP_i|}{|gt|} \\ P = \frac{|TP_i|}{|det_i|} \] 其中，\(gt\) 是整个真实集，且 \(|gt|\) 为真实框的数量，又 \(gt\) 都是真正例，故 \(|gt|\) 也是真实集真正例的数量；\(det_i\) 是当前样本下的预测集，且 \(|det_i|=i\) ；\(TP_i\) 表示当前预测框真正例的集合，且 \(|TP_i| = \sum_i I(f_i为真)\)
最后作出PR曲线
下面举例说明PR曲线的制作。
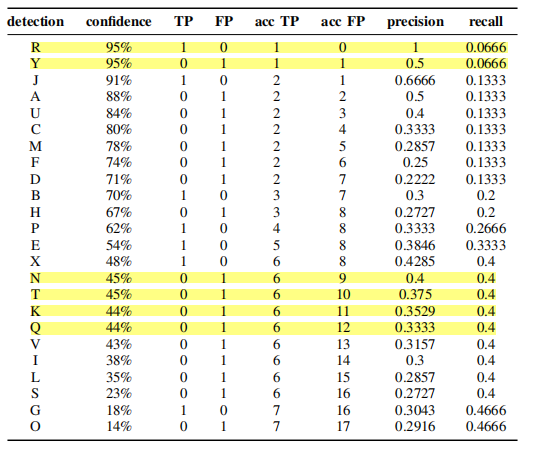
这是一个由15个gt框，24个det框组成的检测结果，TP、FP结果的观测以及P、R结果的计算如下
例如，对于Y点，\(R=1/15=0.0666,P=1/2=0.5\)
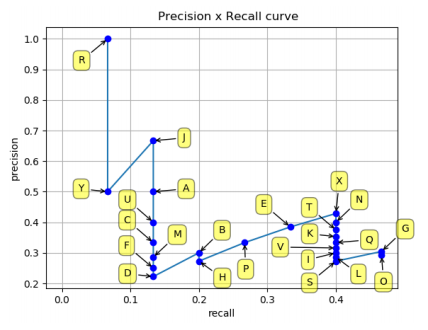
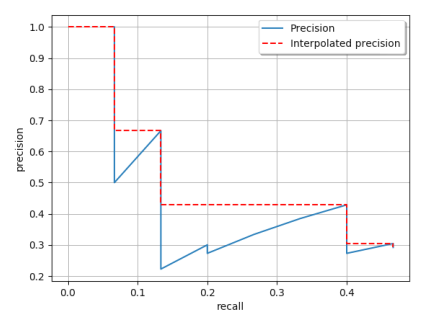
最后作出的PR曲线如下
这种计算方式会存在一个问题，当置信度一致时，不同的排序会产生不一样的结果，例如，上面例子中的R和Y点，如果调换位置，得到PR曲线就会不一样。
2.2. AP
平均精度（Average Precision，AP）是PR曲线下的面积，是目标检测任务最常用的评估指标。
由于PR曲线是锯齿状的曲线，不好直接计算其面积，所以需要取样计算。目前常用的有两种取样方案：
11点插值法（11-point interpolation）。
将 \([0,1]\) 分成10个区间，即 \(\{0,0.1,\cdots,0.9,1\}\)，共11个点，取每个区间中最大的PR值表示该区间的值，然后计算AP值 \[ \mathrm{AP}_{11}=\frac{1}{11} \sum_{R \in\{0,0.1, \ldots, 0.9,1\}} P_{\text {inter }}(R) \\ P_{\text {interp }}(R)=\max _{\tilde{R}: \tilde{R} \geq R} P(\tilde{R}) \]
其中，\(P(R)\) 表示插值操作，即输入一个 \(R\) ，结合PR曲线，预测出一个对应 \(P\)
除了11点插点法，常见的还有101插点法（coco官方比赛使用）等。
所有点插值法（all-point interpolation）。
对所有点进行采样，然后计算AP值 \[ \mathrm{AP}_{\text {all }}=\sum_{n}\left(R_{n+1}-R_{n}\right) P_{\text {interp }}\left(R_{n+1}\right)\\ P_{\text {interp }}\left(R_{n+1}\right)=\max _{\tilde{R}: \tilde{R} \geq R_{n+1}} P(\tilde{R}) \]
下面还是采用上面的例子，说明不同的方法的AP值计算
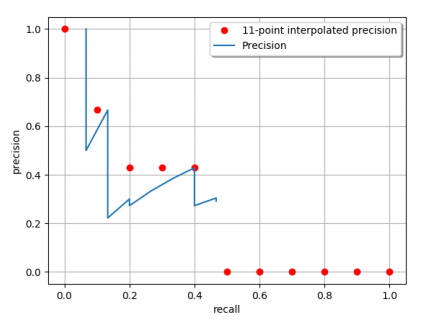
11点插值法。
\[
AP_{11} = \frac{1}{11}(1 + 0.6666 + 0.4285 + 0.4285 + 0.4285) * 100\% = 26.84\%
\]所有点插值法。
\[
AP_{all} = 1 ∗ (0.0666 − 0) + 0.6666 ∗ (0.1333 − 0.0666) + 0.4285 ∗ (0.4 − 0.1333) \\ + 0.3043 ∗ (0.4666 − 0.4) * 100 \%= 24.56 \%
\]
可以看出两种不同方法计算出来的结果是不一样的。所以一般计算AP值前，需要统一计算策略。一般常用11点插值法。
其他衍生指标：
- 均值平均精度（Mean Average Precision，mAP），所有类别的AP的平均值，往往应用于目标检测任务中用于评估算法的性能
- AP_thres，以thres为iou阈值得到的AP值。例如，AP_0.5、AP_50、AP0.5、AP@0.5等，指的都是iou以0.5为阈值计算得到的AP值
- AP_thres1:thres2，从thre1到thres2，以0.05为区间，计算得到的AP集合的均值。例如，AP_0.5:0.95等，指的都是iou分别以 \([0.5,0.55,...,0.95]\) 为阈值，计算得到的AP集合的均值。
- \(AP^{small/medium/large}\)，
3. references
A Survey on Performance Metrics for Object-Detection Algorithms
