1. 输入输出

训练输入： \[ T=\{(x_1,y_1), \cdots,(x_N,y_N)\} \] 其中，

\(x\) 为特征域，\(x_i \in \mathbb{R}^{n},i =1,2,...,N\)
\(y\) 为标签域，\(y_i \in \{1,2\,...,m\}\)

测试输入 \[ X'=\{x'_1, \cdots ,x'_{N'}\},x'_i \in \mathbb{R}^n \] 测试输出： \[ \hat X'=\{\hat x'_1, \cdots ,\hat x'_{N'}\},\hat x'_i \in \mathbb{R}^k \]

2. 模型效果

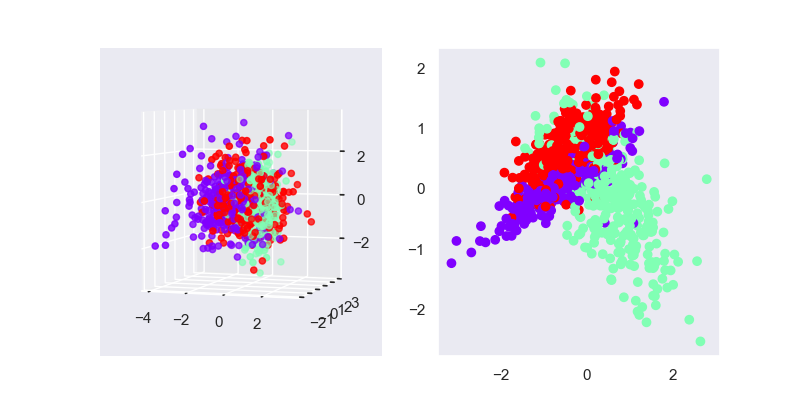
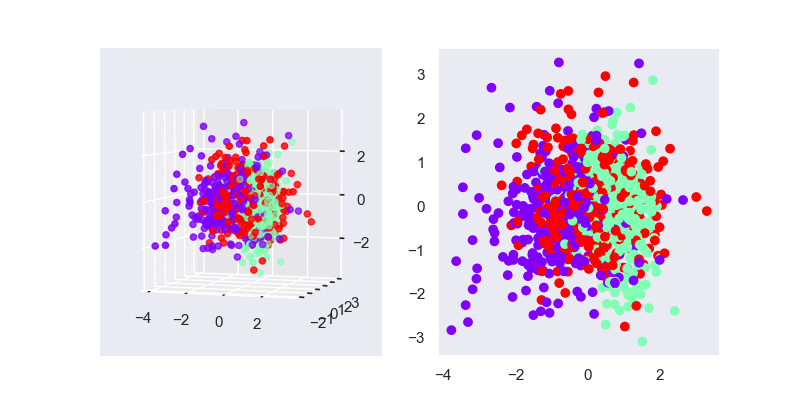
可以看出，LDA降维后仍然保留了大部分类别的信息，可以横向对比下面的PCA降维的结果，PCA降维后的类别信息基本已经丢失了

毕竟LDA是有监督学习，所以一般情况下LDA的效果都是优于PCA的，但PCA的计算速度会比较快。

3. 模型推导

3.1. 基本定义

基本思想和PCA一样，求一个降维后的 \(k\) 维空间 \(W=[w_{ij}]_{n \times k}\)，即可得原样本在 \(k\) 维空间中的投影 \(X'=XW\)

3.2. 学习策略

这里依然沿用聚类的标准作为指导思想：最大化簇间距离，最小化簇内距离。

首先，定义每一个类别的样本中心为该类别样本的均值，则第 \(j\) 类的样本中心为 \[ \mu_j = \frac{1}{N_j} \sum_i^N x_i I(y_i=c_j) \] 其中，\(N_j=\sum_i^N I(y_i=c_j)\)

计算第 \(j\) 类样本间的协方差 \[ \Sigma_j = \sum_i^N (x_i-\mu_j)(x_i-\mu_j)^TI(y_i=c_j) \] 则，第 \(j\) 类的样本中心投影到降维后的坐标系的距离为 \(W^T\mu_j\)；又由前面的PCA中，我们可知第 \(j\) 类内的紧密程度可以表示为 \(W^T\Sigma_jW\)

根据分类的指导思想，可得目标函数 \[ J(W) = \frac{\sum_j^n \|W^T\mu_j - W^T\mu\|_2^2}{\sum_j^n W^T\Sigma_jW} = \frac{W^TS_bW}{W^TS_wW} \] 其中，\(\mu=\frac{1}{N}\sum_i^N x_i\) 为所有样本的均值，簇间散度矩阵 \(S_b=\sum_j^n N_j(\mu_j-\mu)(\mu_j-\mu)^T\) ，簇内散度矩阵 \(S_w=\sum_j^n \Sigma_j\)（后面的 \(\Sigma_j\) 是协方差矩阵）

但上式最终结果是一个矩阵，并非标量形式，无法进行优化。一种常见的转换做法是取矩阵的主对角线上的值的累乘结果作为最终的标量结果，即最终的目标函数为 \[ J(W) = \frac{\prod_{diag} W^TS_bW}{\prod_{diag}W^TS_wW} = \prod_i^k \frac{w^TS_bw}{w^TS_ww} \]

3.3. 学习算法

和PCA中求解思路一样，求解上诉目标函数的最优解，即求解 \(J(w)=\frac{w^TS_bw}{w^TS_ww}\) 的前\(k\)个最大值

可以看出，\(J(w)\) 符合广义瑞利商的形式（关于瑞利商的相关介绍，可以参考我之前的这篇笔记，这里就不再赘述），所以，\(J(w)\) 的前\(k\)个最大值为 \(S_w^{-1}S_b\) 的前 \(k\) 个最大特征值

最终的算法流程总结如下

计算每个类别的样本中心 \(\mu_j = \frac{1}{N_j} \sum_i^N x_i I(y_i=c_j)\)，计算所有样本的样本中心 \(\mu=\frac{1}{N}\sum_i^N x_i\)
计算每个类别的样本间的协方差 \(\Sigma_j = \sum_i^N (x_i-\mu_j)(x_i-\mu_j)^TI(y_i=c_j)\)
计算簇间散度矩阵 \(S_b=\sum_j^n N_j(\mu_j-\mu)(\mu_j-\mu)^T\)
计算簇内散度矩阵 \(S_w=\sum_j^n \Sigma_j\)
计算 \(S_w^{-1}S_b\) 的前 \(k\) 个最大特征值及其对应的特征向量 \(w\)，并以此作为列向量，组合成矩阵 \(W=[w_{ij}]_{n \times k}\)
输出 \(X'=XW\)