1. 分形的概念
分形(Fractal)一词是美国数学家 Mandelbrot先生(1924-2010) 创造出来的,此词源于拉丁文形容词fractus,对应的拉丁文动词是frangere,意思为不规则、支离破碎等。
美籍华人数学家陈省身先生认为几何学可分为以下阶段:
- 第一阶段:公理(欧几里德)
- 第二阶段:坐标(笛卡尔、费马)
- 第三阶段:微积分(牛顿 菜布尼兹)
- 第四阶段:群(克莱因、李)
- 第五阶段:流形(黎曼)
- 第六阶段:纤维丛(嘉当、惠特尼)
- 第七阶段:分形几何(曼德勃罗特)
所以分形几何是二十一世纪的几何。但目前分形工程上的应用并不多,现在主要应用于作图方面。
网上对于分形的科普文章已经很多了,本人对分形的研究也不是很深入,所以这里就只是简略地介绍一些分形知识的皮毛,属于是班门弄斧了。
2. 分形的特征
一般来说,分形都具有以下三个重要的特征。
2.1. 无限次递归
分形是经过无数次递归迭代后的结果。这意味着,分形具有无穷多的层次和细节,可以被无限放大、永远都有结构。也就是说,只要是能够画出来的图形,都不是真正的分形,因为我们不能画出具有无穷多细节的图案。
这引申出一个重要的概念,对于二维分形图案,其面积会趋于一个极限值,但其边长会趋于无穷大。
应用这个概念的例子有著名的英国海岸线测量问题——测量精确越高,英国海岸线的长度也会不断趋于无穷。
2.2. 自相关性
一个系统的自相似性是指某种结构或过程的特征从不同的空间尺度或时间尺度来看都是相似的,或者某系统或结构的局域性质或局域结构与整体类似。
例如,下图中的分形龙,就可以看成是由四个相似的缩小了的分形龙组成。
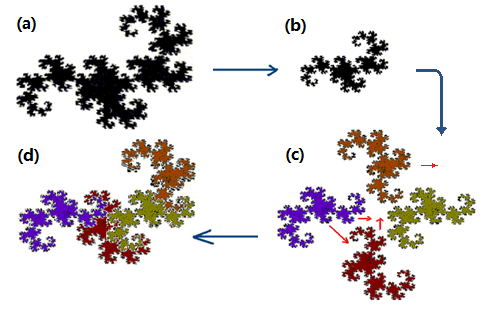
2.3. 分数维
像上面提到的分形龙,是由一维的线条经过无数次迭代生成的。当迭代次数越多的时候,一维的线条逐渐充满了二维的空间,那这个图案究竟是一维的,还是二维的呢?
传统的几何学认为,维度即空间中可以确定任何一点位置所需要变量的数量。例如,空间中的三维,就是确定一个点的需要三个数值:经度、纬度、和高度。
对于这种定义维度的方式,维度只能是整数的,但维度可不可以是分数呢?
豪斯多夫从物体的自相似性来定义维度,提出了豪斯多夫维数,定义为 \[ d = \frac {\ln M} {\ln N} \] 其中,N表示缩小比例,M表示原物体由M个缩小后的物体拼接的。
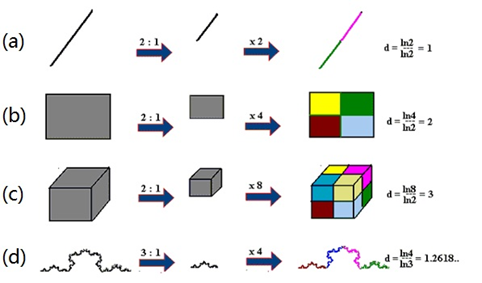
另外,上面提到的英国海岸线测量问题中,根据多次测量所得的结果,英国海岸线的分形维数约为1.25。
3. 分形的分类
这里,我个人按照是否由线性迭代生成的,把分形分成两类——几何分形和混沌分形
3.1. 几何分形
几何分形一般由二维线集或面集组成,混乱程度较低,一般是由线性迭代而成,即使改变一个参数,整体图案可能也不会有太大的变化。
更多的分形图案可以查看我的另一篇博文:图赏-几何分形
下面分享下几何分形的绘图技巧。
3.1.1. 递归体设计
几何分形绘图最重要就是如何去设计画线路径,因为整体路径是由一个基础的递归循环体不断递归而来,所以问题转化为如何设计递归循环体,通常使用LS( L-System)文法生成递归体。
PS:LS文法只适用于由线集组成的分形,不适用于由面集组成的分形
LS文法规则:
- F:以当前方向前进一步,并画线;
- f:以当前方向前进一步,不画线;
- +:逆时针旋转角;
- -:顺时针旋转角;
- [:表示暂时保存当前的画图状态;
- ]:表示提取出保存的画图状态。 “[”和“]”要成对的出现。
上面的分形龙的绘图路径用LS文法表示为
{'s': 'Fr', 'r': 'r+lF+', 'l': '-Fr-l'}上述语句阅读步骤为:
- 首先跳转到值为
s的key。 - 遍历对应key的value值。
- 对于每个遍历的字符,会先查询是否有与该值相同的key值。
- 如果没有,则把该字符拼接到路径后面。
- 如果有,则跳转到对应的key,重复2-5步骤,直至达到最大迭代深度。
例如,上诉语句,迭代两次后的路径为Fr+lF++-Fr-lF+,忽略掉r和l,实际路径为F+F++-F-F+
3.1.2. 绘图包选择
基于Python的绘图,可供选择的绘图包有matplotlib、turtle、tkinter。
使用turtle包绘图代码传送门
使用matplotlib包绘图代码传送门
使用tkinter包绘图代码传送门
网上大多使用turtle绘制分形,因为用turtle作这种轨迹图比较直观、简单,而tkinter一般用于GUI交互式设计,用在这里有点牛刀小用了。我一般用matplotlib,毕竟matplotlib是信仰啊!🙆♂️
3.2. 混沌分形
混沌分形一般由一维点集组成,混乱程度较高,一般是由非线性迭代而成,一般都会有一个迭代公式,可能其中一个的参数变化了,整个图案都会有翻天覆地的变化。
混沌分形的图案一般都比几何分形的图案更加壮观美丽。
更多的分形图案可以查看我的另一篇博文:图赏-混沌分形
下面列举一些比较经典的混沌分形
3.2.1. Mandelbrot 集
论及分形,必须要提到Mandelbrot 集
Mandelbrot 集被称为“上帝的指纹”、“魔鬼的聚合物”,据说其拥有世界上所有物体的形状,真正意义上的包罗万象。
Mandelbrot 集迭代公式 \[ z_{n+1} = z_n^2 + C \] 其中,\(z_n\)和\(C\)都是复变量。
对于复平面上任一个点 \((x, y)\) ,代入和\(C\)中,并使\(z_0=0\),然后不断迭代。如果这个点不发散,则将其收集起来。最后,复平面上所有不发散的点的集合就是Mandelbrot 集。
M集有几个特征:
- 集合中的所有点的模(长度)小于2,所以当迭代过程中,模长大于2时,我们就可以认为这个点是发散的。而且实际上,复平面的取值范围为\(x \in (-\sqrt{2}, \sqrt{2}), y \in (-\sqrt{2}, \sqrt{2})\)
- 对应发散的点来说,可以使用模长大于2时的迭代次数来表示该点的发散性,也就是我们可以利用这个发散性进行不同的配色方案。这里有一个常用的配色方案,传送门
- 集合的面积目前还没有一个准确的答案,目前有通过复分析收敛的方法,但是计算次数太多,需要的精度太高了。最简单的方法就是通过数像素点,当然这种方法也只能得到一个大概的值。目前通过数像素点方式算出来的结果大概是1.5左右
- 集合中有一些比较特殊的点,如下图所示

其中,点1被称为 Seahorse Valley (海马山谷)点2被称为 Elephant Valley (象谷),点3被称为 Triple Spiral Valley (三重螺旋)。
| Seahorse Valley | Elephant Valley | Triple Spiral Valley |
|---|---|---|
 |
 |
 |
3.2.2. Julia 集
Julia 集和 Mandelbrot 集的迭代式是一样的,但在Mandelbrot 集中,C值为复平面上的任一个点,在 Julia 集中,C值是事先给定的。所以 Julia 集是 Mandelbrot 的一部分,下面是Julia 集在Mandelbrot 集中的分布图。

遍历每一个取值范围内的C值,得到的下图效果

PS:比较有趣的是,Julia 集这个概念是Julia(法国数学家(1893-1978))提出来的,但真正实现出来的是 Mandelbrot 。其实,两人并非同一个时代的人,Julia 集这个概念提出来的时代,科技水平并足以支撑完成迭代计算。后来 Mandelbrot 进入了IBM公司,才借助计算机实现这一概念。
3.2.3. IFS系统
IFS(Iterated Function System),迭代函数系统,是分形的另一个重要的分支。
IFS利用分形的自相关性的性质,常用于图像压缩。分形图像压缩的解码速度很快,但编码速度慢,比较适合一次写入、多次读出的文档。
不同于上面的 Julia 集和 Mandelbrot 集通过收集一定迭代次数内收敛的点,IFS系统每隔一定的迭代次数就会收集当前点,可以理解为点的轨迹的集合。IFS系统迭代公式为 \[ \begin{aligned} F_i \left ( \begin{array}{ll} x_{n+1} \\ y_{n+1} \end{array} \right ) &= \left ( \begin{array}{ll} a_i \quad b_i \\ c_i \quad d_i \end{array} \right ) \left ( \begin{array}{ll} x_n \\ y_n \end{array} \right ) + \left ( \begin{array}{ll} e_i \\ f_i \end{array} \right ) | p_i \\ &= \left ( \begin{array}{ll} r_i \cos \theta _i \quad -q_i \sin \phi _i \\ r_i \sin \theta _i \quad \quad q_i \sin \phi _i \end{array} \right ) \left ( \begin{array}{ll} x_n \\ y_n \end{array} \right ) + \left ( \begin{array}{ll} e_i \\ f_i \end{array} \right ) | p_i \end{aligned} \] 对于式中的仿射变换系数,\(e\)、\(f\)为子图相对于原图平移量,\(\theta\)、\(\phi\)为子图相对于原图的旋转量,\(r\)、\(q\)为子图相对于原图缩放系数。
IFS系统有以下特征:
- 对于每次迭代,都要进行一次线性变换并接上一个平移,我们说这是仿射的。
- 为了保证系统是收敛的,所以仿射变换一定是压缩映射。任意图形经过仿射变换后,面积为变换前的\(|ad-bc|\)倍,这里有\(|ad-bc|<1\) 。IFS将待生成的图像看做是由许多与整体相似的(自相似)或经过一定变换与整体相似的(自仿射)小块拼贴而成。所以,IFS是完备度量空间中的一个收缩映射的有限集。
- 仿射变换系数会有多组取值,每组取值都会有一个概率,我们称这是带概率的IFS系统,并把所有取值的集合称为IFS码。每次迭代的时候,按照概率选取一组取值进行仿射变换。所以,对于某一时刻的迭代,是线性的,但对于整个过程的迭代,是非线性的。
下面有具体例子说明下IFS系统是怎样工作的。
例如,sierpinski三角的IFS码为
# [a - f, p]
[[.5, 0, 0, .5, 0, 0, 1. / 3.], # 1
[.5, 0, 0, .5, .5, 0, 2. / 3], # 2
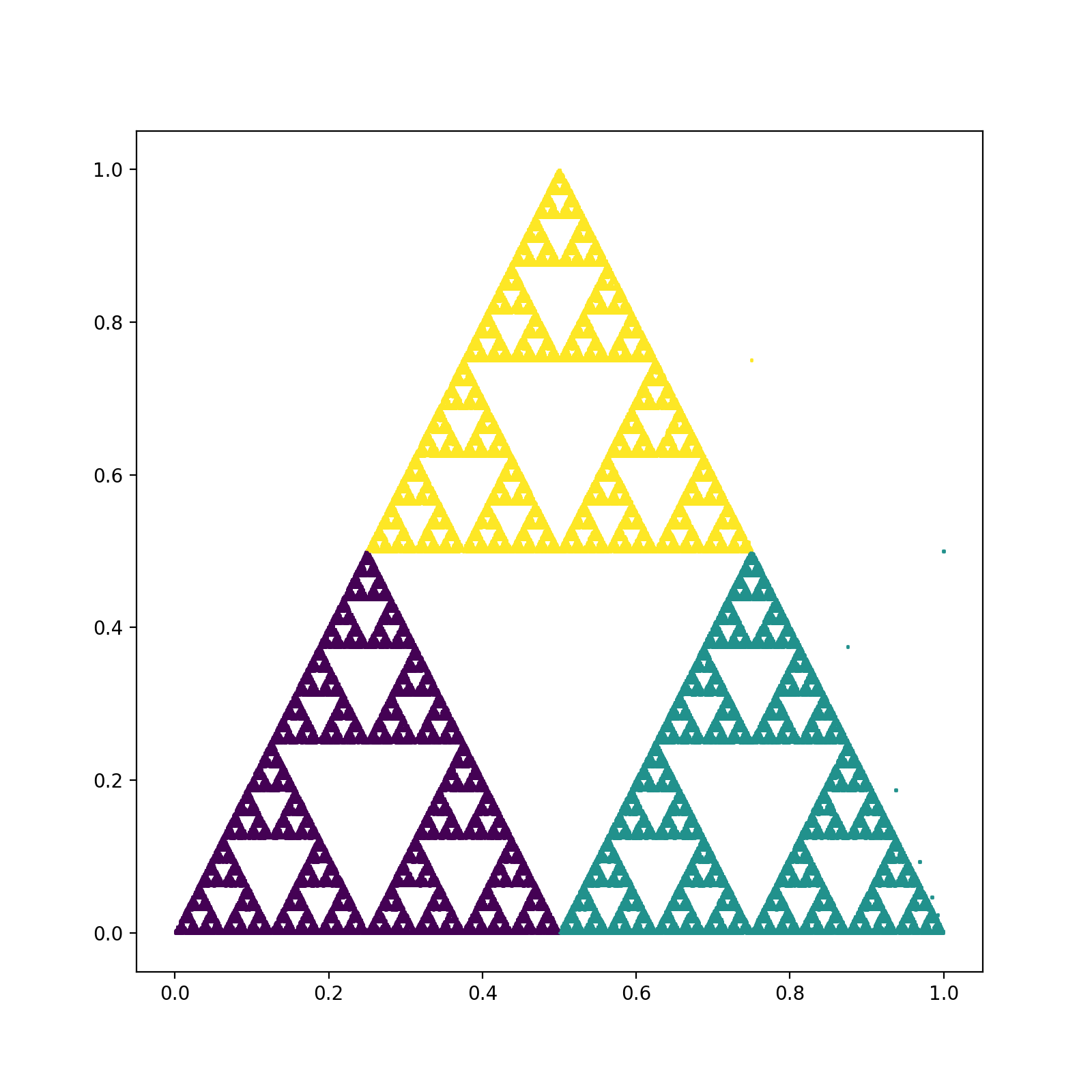
[.5, 0, 0, .5, .25, .5, 1]] # 3为这3组取值分别配上紫色、绿色、黄色,作出来的图如下所示
可以看到,每一组取值都会形成一个缩小版的自相关的图案。
又因为sierpinski三角由3个自相关的缩小的图案拼接而成,刚好对应IFS码中的三组取值。
接着我们修改IFS码的概率,修改为
# [a - f, p]
[[.5, 0, 0, .5, 0, 0, .1], # 1
[.5, 0, 0, .5, .5, 0, .4], # 2
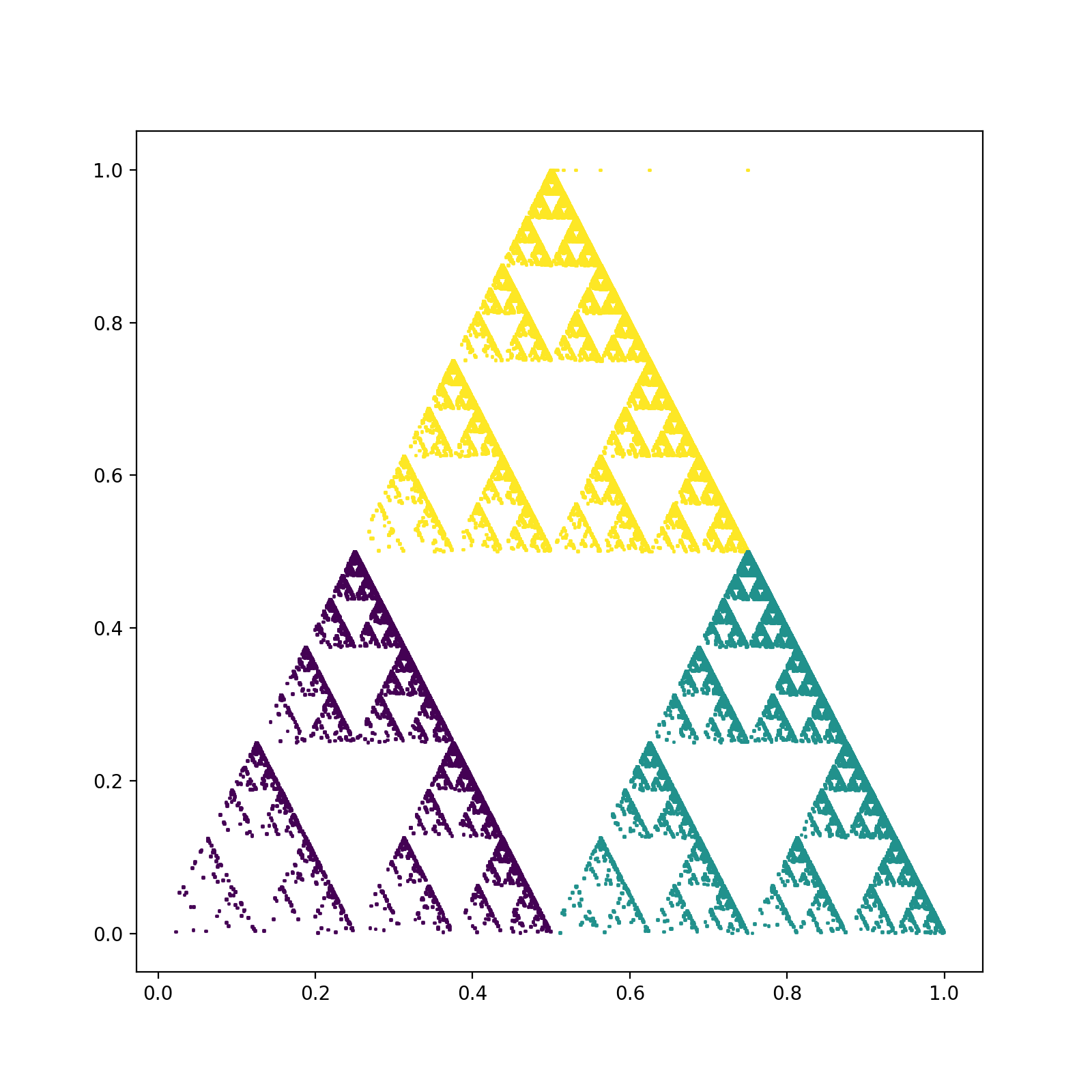
[.5, 0, 0, .5, .25, .5, 1]] # 3作出来的图案如下所示:
可以看出来,IFS码的概率影响每个点分布情况。由于第一组取值概率最小,所以分布在靠近左下顶点处的点较少,同理,其他位置也如此分析即可。
基于上面这个规律,我们可以粗略地给出IFS码的设计步骤,为方便描述,我们以sierpinski三角的IFS码设计为例进行说明。。
构想出一个原始的分形图案,我们不妨称之为分形元,这里的分形元就是最大的那个三角形;
确定总图案是由多少个由分形元缩放仿射变换拼接而成的,与之对应的,我们就应该设计多少组仿射变换系数,这里因为是由3个自相似的图案构成的,所以我们需要设计3组系数;
因为每一组系数是独立的,所以下面只以第一组系数(即紫色部分)的设计为例,其他系数如法炮制即可;
确定\(r\)、\(q\):\(r\)、\(q\)分别对应xy方向的缩放比例,这里都是缩小了一般,故\(r=0.5,q=0.5\)
确定\(\theta\)、\(\phi\):\(\theta\)、\(\phi\)分别对应xy方向的旋转角度,这里没有进行旋转,故\(\theta=0,\phi=0\)
确定\(e\)、\(f\):\(e\)、\(f\)分别对应xy方向的平移距离,这里没有进行平移,故\(e=0,f=0\)
确定取值概率\(p\):\(p\)对应点的分布情况,这里是平均分布,故\(p=\frac{1}{3}\)
代入式中即可设计出第一组系数
[.5, 0, 0, .5, 0, 0, 1. / 3.],循环步骤4-7既可得到其他组的系数。
由于sierpinski三角是比较规则和简单,所以上面设计略为简单。但其实对于一些较为复杂的图案,旋转、平移、缩放量有时是很难看出来的,所以各系数是较难设计的,而且得不断调参才能得到充满艺术感的图案,这一点跟深度学习调参炼丹是很像的。
关于IFS系统,还有一个分支——分形火焰算法(The Fractal Flame Algorithm ),这个我也没大弄懂,这里先mark一下,日后有时间再补吧👻~