1. 二维函数表现形式
1.1. 坐标系
1.1.1. 平面直角坐标系
平面直角坐标系就是我们平常接触到最多的xy坐标系,这部分函数的作图没什么好说,直接按规则作图就是了。
1.1.2. 特殊坐标系
对于基于特殊坐标系的函数,需要按照一定的坐标变换规则将其重新映射回平面直角坐标系中。这里重点介绍常见的基于极坐标系的函数的作图。
对于任意基于极坐标系的函数,有
\[ f(r, t)=0 \]
进行如下变换 \[ \left \{ \begin{array}{ll} x = r \cos {t} \\ y = r \sin {t} \end{array} \right . \]
最后作出x-y图即可。
1.2. 多重变量函数
1.2.1. 显函数
显函数只有单一自变量,函数表现形式为
\[ y = f(x) \]
或 \[ \left \{ \begin{array}{ll} x = f(t) \\ y = f(t) \end{array} \right . \] 这种形式的函数是很容易作图的,只要给出自变量的序列,代入函数式求出因变量的序列,即可作出函数图像
1.2.2. 隐函数
二维隐函数具有两个自变量,一般函数形式为 \[ f(x, y) = 0 \] 这种函数并不能通过指定一个自变量序列去完成作图,我们得找到一个符合函数式的\((x,y)\)集合。
诚然,可以指定两个自变量序列,对两个序列进行交叉组合形成\((x,y)\)集合,分别代入函数式中计算,把所有符合结果的 \((x,y)\) 组合记录下来,最后作出函数图像。
这种方法的弊端也非常明显:
- 程序的时间复杂度高。如果我们需要作出比较精细的函数图像,那我们需要一个间隔非常小的xy序列,遍历这两个序列的时候,需要计算的资源的太大了。
- 并不能保证找到满足函数的xy组合。我们很难指定一个足够小的xy序列,保证所有满足函数式地点都被记录下来,其实,很多情况下,我们是得不到满足函数式的xy组合的。
一种优化方案是将原函数式变换为\(|f(x, y)|<\varepsilon\)的形式。
这种方法的确可以画出图像的大致轮廓,但这种方法作出的图像的线条并不均匀。具体表现为在梯度上升较快的区域,线条会很细;在梯度上升较慢的区域,线条会很粗。当指定的\(\varepsilon\)较小时,有部分的线条甚至会做不出来;当指定的\(\varepsilon\)较大时,会出现有线条粘连在一起的情况。
所以,我们得寻找更加高效、准确的隐函数作图算法。
2. 隐函数作图算法
2.1. 调包法
这个就比较简单了,直接调用现成的包即可。
2.1.1. matplotlib
调用 matplotlib 的 contour 函数,其原理是把函数扩展为三维函数\(z=f(x,y)\),然后做\(z=0\)的等高线,目前猜测使用的是 marching squares 算法,这个算法下面还会进行介绍。
2.1.2. sympy
调用 sympy 的 plot_implicit 函数,其用到的算法是 (Tupper)interval arithmetic,这个算法下面还会进行介绍。
2.2. 梯度法
这其实是上面 \(|f(x, y)|<\varepsilon\) 方法的一种改进方案。其函数式为 \[ \frac{|f(x, y)|}{|\nabla f|} < k \] 其中,k值我将其称为精细程度,k值越小,线条展现越精细,反之,线条展现越粗犷,一般这个值设为1
这种方案的优点是去除了梯度变化对线条粗细的影响,而且所需要xy序列规模并不需要太大。
其缺点是,k值无法自动调节,使得图像的具有一个较好的表现效果。
2.3. Marching squares
Marching squares 算法用来生成二维图像,Marching cubes 算法用来生成三维图像,两个算法的思想是一样的。
Marching squares 算法的流程为:
- 分别生成一个xy序列,然后对每一个xy序列交点代入函数中求值,得到一个函数值分布的二维数组。
- 用一个2x2的窗口遍历这个二维数组。
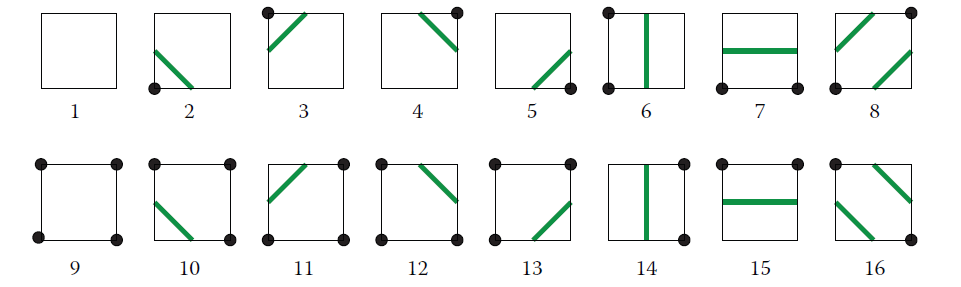
- 对于每一个遍历的窗口数组的四个顶点,大于0的为 Positive grid(下图中标黑的点),不大于0的为Negative grid(下图中没标黑的点)。
- 一共可以组合成下面16种不同的情况,根据每种情况,返回下列对应情况的轮廓线。
- 最后窗口遍历完整个二维数组的时候,把所有轮廓线组合在一起,整个函数的图像也就做出来了。
另外,下面两种特殊情况用上面的算法会绘制错误。
- 对于曲面函数\(z=f(x, y)\),如果该函数在某个区域内是非连续的,那么\(f(x, y) = 0\)在该区域内就会绘制错误
- 对于曲面函数\(z=f(x, y)\),如果该函数在某个区域内是一个最大值或最小值为0的凸函数,即该函数与\(z=0\)的xy平面相切,如果相切的是一个平面,而不是一个点,那么\(f(x, y) = 0\)在该区域内就会绘制错误
当然上面两种情况出现的概率较小,暂且可以忽略。
最后,下面还有一些编程上的小trick
2.3.1. 巧用mask
如果把窗口数组的每种情况都写成判断语句,程序运行效率低,而且代码冗长,一点都不优雅。
我们可以先对窗口数组所有小于0的值置为0,所有大于0的值置为1,然后设计一个2x2的mask数组,与窗口数组进行乘法运算,使用一个map来把结果值与16种情况一一对应起来。
这里,我设计了一个mask数组[[2, 3], [4, 5]]。为什么要这么设计?可以发现,2、3、5是互质的,虽然2和4非互质,但在这里,因为不能重复取,所以事实上,在这里,2、3、4、5是互质的。
故这四个数所有组合的乘积结果都是唯一的。因此我们可以对上面16种情况进行编码,然后使用数组的累乘值进行索引判断即可。
例如,现在有一个变换后的窗口数组[[0, 0], [1, 1]],与mask相乘后得到结果数组[[0, 0], [4, 5]],然后把结果数组中为0的值置为1,得到[[1, 1], [4, 5]],对这个数组的每个元素累乘后得到该窗口的位置值20,如果第14中情况的索引值为20,即可知其对应第14种情况了。
2.3.2. 尽量少使用外循环运算
直接使用python的循环语法进行遍历运算是很慢的,所以这里我设计成使用numpy先运算再分割的方案,而不使用先分割后运算。
具体的,对mask数组由原来的shape为(2, 2)变换为(4, 1),然后把axis=-1的shape广播为二维数组的shape。这样变换后,两个数组可以直接相乘。当然得到的数组,需要经过位置对齐后,才能得到结果数组。
例如,现在有一个二维数组,其shape为(300, 400),那么其mask数组为(4, 300, 400),两者相乘后的结果数组为(4, 300, 400),然后对于axis=0的每一个数组裁剪再拼接后,得到shape为(4, 299, 399)的结果数组,然后对结果数组axis=0进行累乘,最后得到shape为(299,399)的位置数组。
2.4. (Tupper)interval arithmetic
区间算法,这个算法可用于任意方程的图像作图,属于万金油般的作图算法。
其作者Jeff Tupper就在他的作图软件GrafEq中运用了这个算法,做出来的函数图像相当不错,后面也会介绍一下这个作图软件。
这个算法的思想是:
- 证明函数\(f(x, y)=0\)在指定区间内穿过0点,或者证明这个函数在这个区间内没有穿过0点。
- 把整个屏幕涂成红色(当然这个颜色可以自己设定);
- 把屏幕分为若干个区间,遍历每个区间,对每个区间循环进行步骤4-6;
- 证明函数在区间内没有穿过0点,证明的方法是,对于函数 \(f(\langle x_0, x_1 \rangle,\langle y_0, y_1 \rangle)=\{ \langle l, r \rangle , \langle b, t \rangle \}\) 的结果区间差值的判定值为 \(\langle False, False \rangle\) ,如果可以证明,则把该区间涂成白色,跳出循环;
- 证明函数在区间内穿过0点,证明的方法是,函数 \(f(\langle x_0, x_1 \rangle,\langle y_0, y_1 \rangle)=\{ \langle l, r \rangle , \langle b, t \rangle \}\) 的结果区间差值判定值为 \(\langle True, True \rangle\) ,且在 $[x_0, x_1]*[y_0,y_1] $ 区间内连续。如果可以证明,则把该区间涂成黑色,跳出循环;
- 如果两者都不能证明,则把该区间均分为4个区间,对每个区间递归重复步骤4-6,直至超过设置的递归最大深度,则放弃这个区间,跳出循环。
- 最后在画布上,白色区域一定不是函数的图像,黑色区域一定是函数的图像,红色区域可能是也可能不是函数的图像。延伸开来,对于不等式来说,黑色区域就是函数的填充部分,红色区域就是函数的轮廓;对于隐函数等式来说,函数的图像是红色的区域,因为隐函数等式的图像一般都是不确定的。
上面流程中,有两个关键的地方:
\(f(\langle x_0, x_1 \rangle,\langle y_0, y_1 \rangle)\) 的计算问题。这种带区间的运算需要对运算符号进行重定义。例如,计算 \(\mathrm{Subtract}(\langle a, b \rangle, \langle A, B \rangle)\) ,其返回区间为 $a-B, b-A $
在 $[x_0, x_1]*[y_0,y_1] $ 区间内的连续判定问题。这个需要判定定义域和值域的范围。
另外,作者在原论文中对浮点型数值取值引入了 "rounding up and down" 的概念,即通过向上/向下取余来保留n个小数位,由此把取值期间划分为 "inner bounds" 和 "outer bounds"。
对于这样的取值方案,作者解释是,当划分的区间很大的时候,传统的四舍五入的取值方案带来的误差会很大。
个人感觉提出这种解决方案的是囿于当时计算机的硬件水平,但在现在,感觉就有点画蛇添足了。而且,我在阅读 sympy 的源码的时候,sympy 的作者也没有采用这种取值方案,认为这是没有必要的。
3. 效果比较
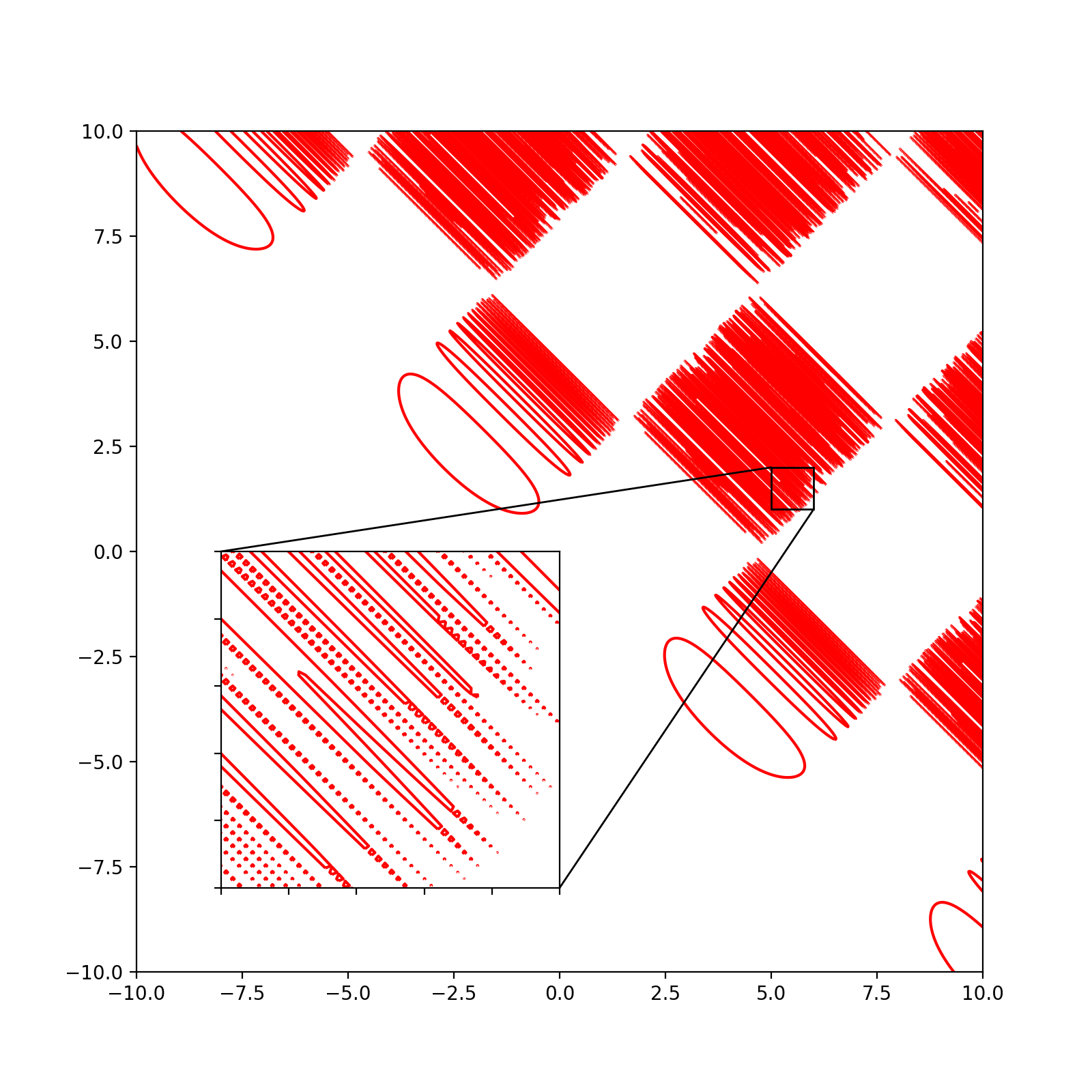
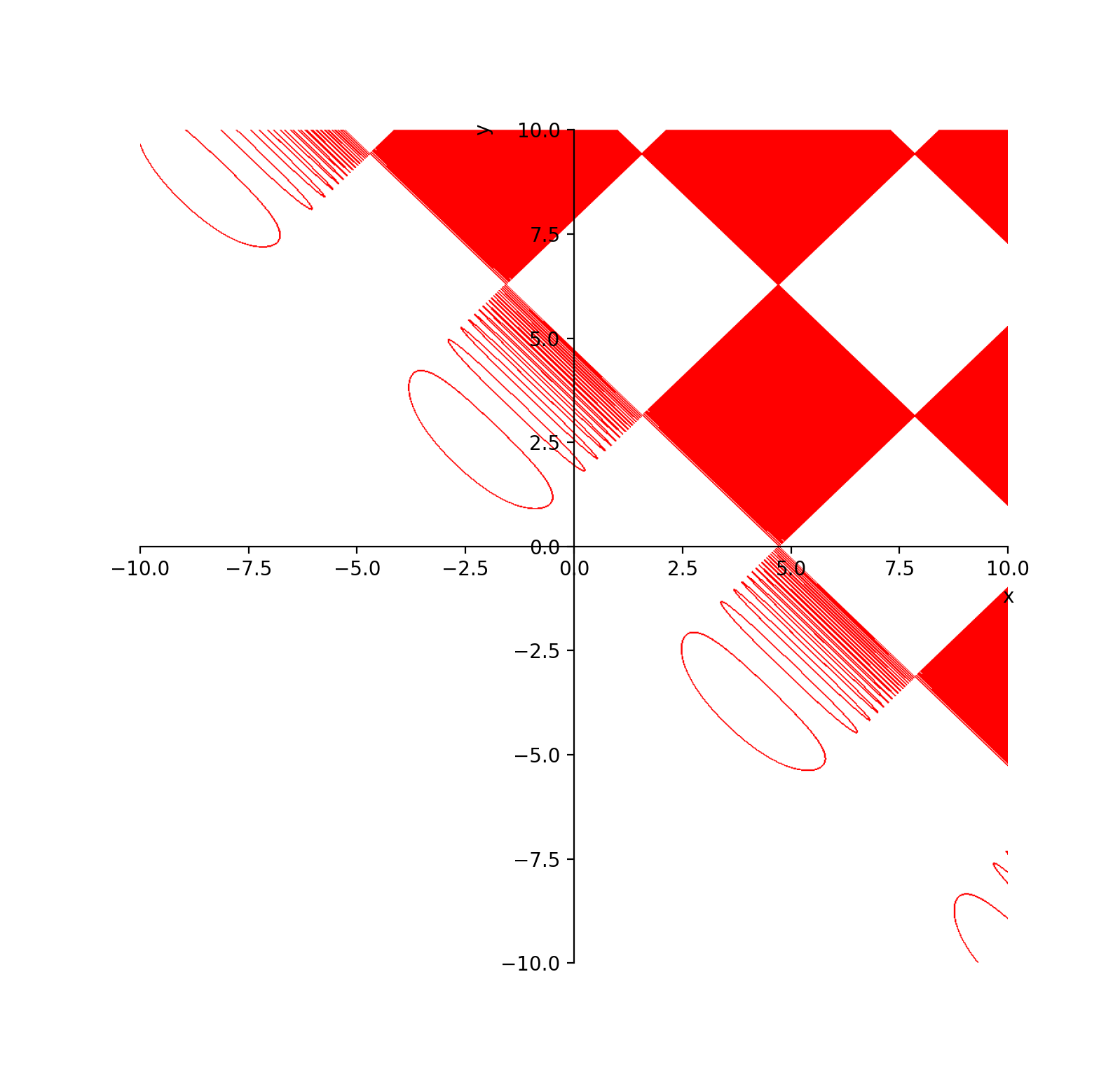
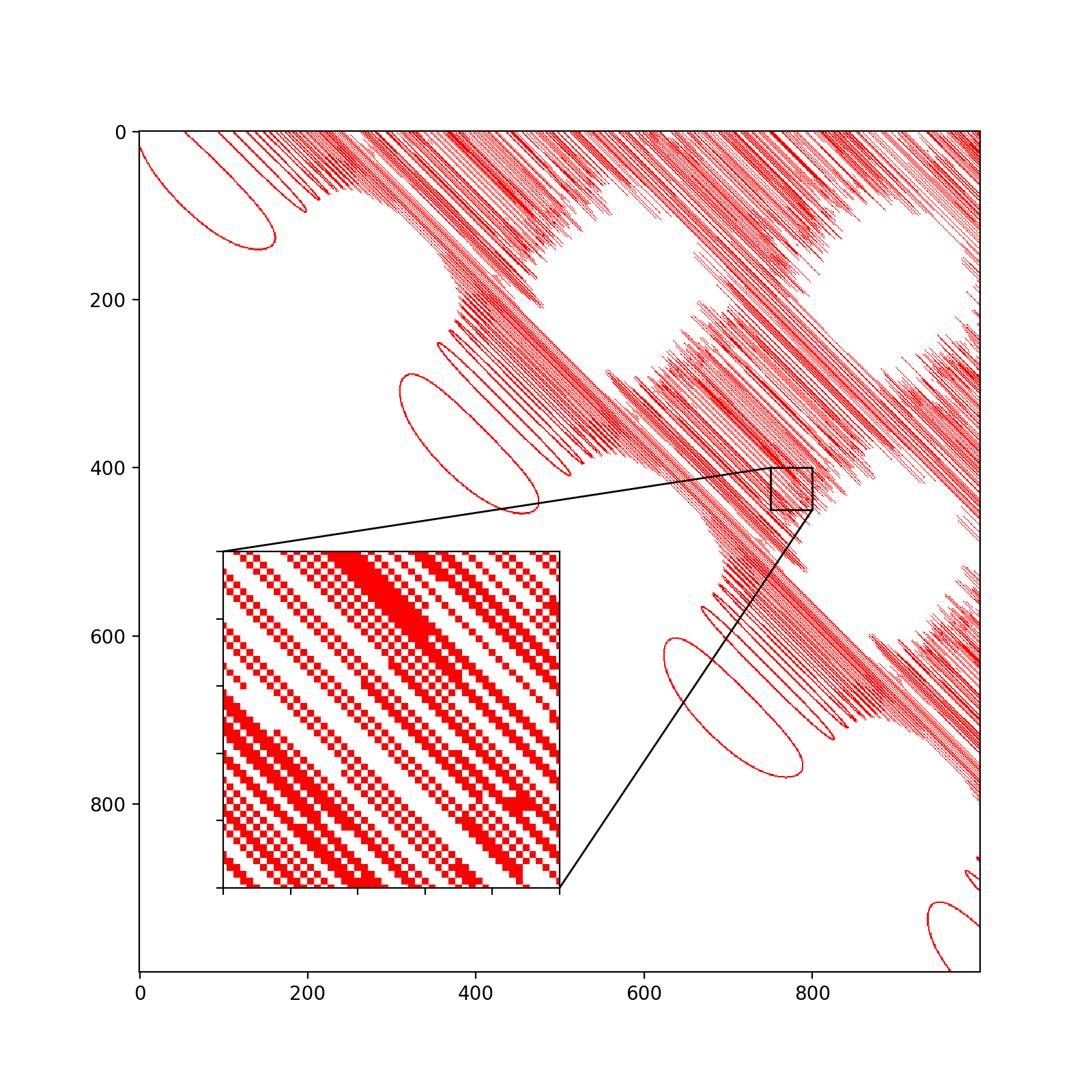
从上面可以看得出来,
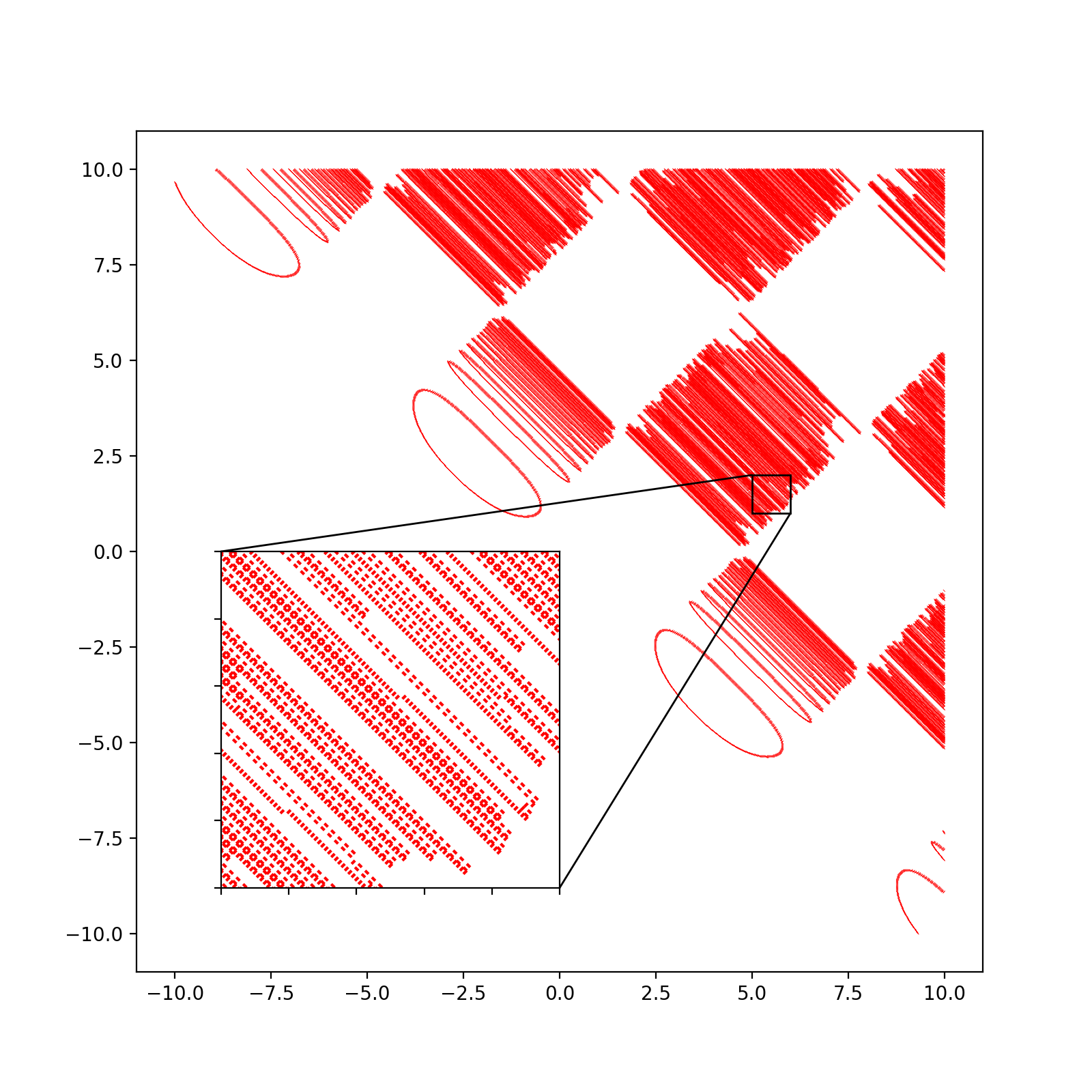
效果最好的是调用 sympy 包作出来的图像,图像的线条相当精细,可见 interval arithmetic 算法的优越性,但用这个算法作图时间有点长,而且这个包对于图像的个性化设置很少,不太喜欢用。
效果最差的就是梯度法作出来的图像,这种方法做出来的图像线条会有一种不连贯,线条比较杂的感觉,但其实这种方法画一些精细程度要求不高的图的时候,作出来的图像还是可以的。
使用 matplotlib 作出来的图和使用 marching squares 算法作出来的图像是差不多的,而且放大后细节呈现上也是差不多的,所以我估计 matplotlib 的 contour 函数也是用的 marching squares 算法,但从运行速度的角度看,明显可以感受到 matplotlib 作图比我自己写程序作图的速度是要快得多,可能 matplotlib 加了些其他优化处理,日后有时间再研究研究 matplotlib 的源码。
4. 其他作图软件
4.1. GrafEq
这个软件是Matrix67大神极力推荐的作图软件,这是这个软件的下载地址,但这个软件年代比较久远,也很久没更细了,Windows10经过测试,可以安装成功,但不支持MacOS 9.2以上的版本。
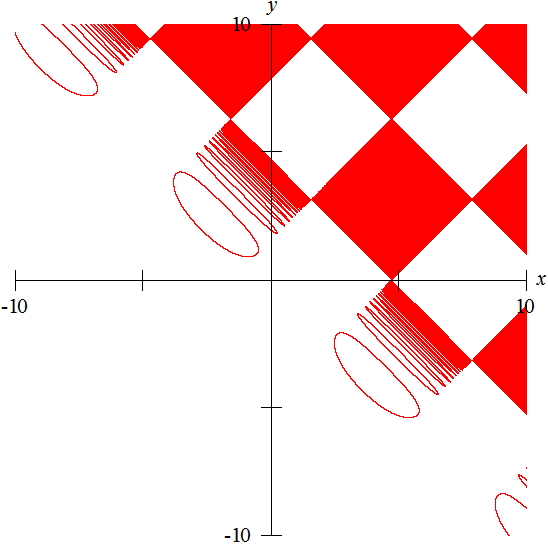
下面是这个软件作出来的图像
4.2. grapher
这个是Mac自带的绘图软件,个人用起来感觉还不错,而且功能也挺强大,除了作二维的函数图,还可以作3维图像。而且3维图像的表现效果相当不错。
下面是这个软件作出来的一些图像
5. reference
Marching squares & Marching cubes
Reliable Two-Dimensional Graphing Methods for Mathematical Formulae with Two Free Variables