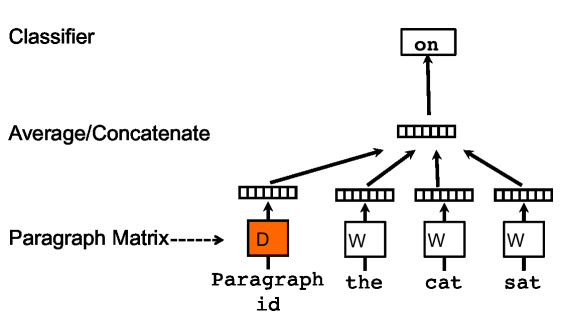
基于numpy的实现代码传送门
1. 输入输出
Input:
样本序列 \[ X=(\vec x_1,...,\vec x_n) \] 其中,\(\vec x_i \in \mathbf R^V\)
Output:
编码序列 \[ \hat X=(\hat {\vec x}_1,...,\hat {\vec x}_n) \]
其中,\(\hat {\vec x}_i \in \mathbb R^N\)
特别地,一般上有 \(V>N\) ,所以word2vec也可以看做是对原编码矩阵的一种降维方法。
另外,对于常见的神经网络模型,一般都是以输出层的输出 \(y\) 作为模型的最终输出,但这个值代表的是每个单词的输出概率,而我们想要得到的每个单词的向量表示,所以输入权值矩阵作为最终输出。当然也有使用输入权值矩阵和输出权值矩阵相结合的输出,具体可参见论文Using the Output Embedding to Improve Language Models 。
2. 算法推导
2.1. 基本框架
word2vec本质上就是一个神经网络模型,基本的模型框架如下
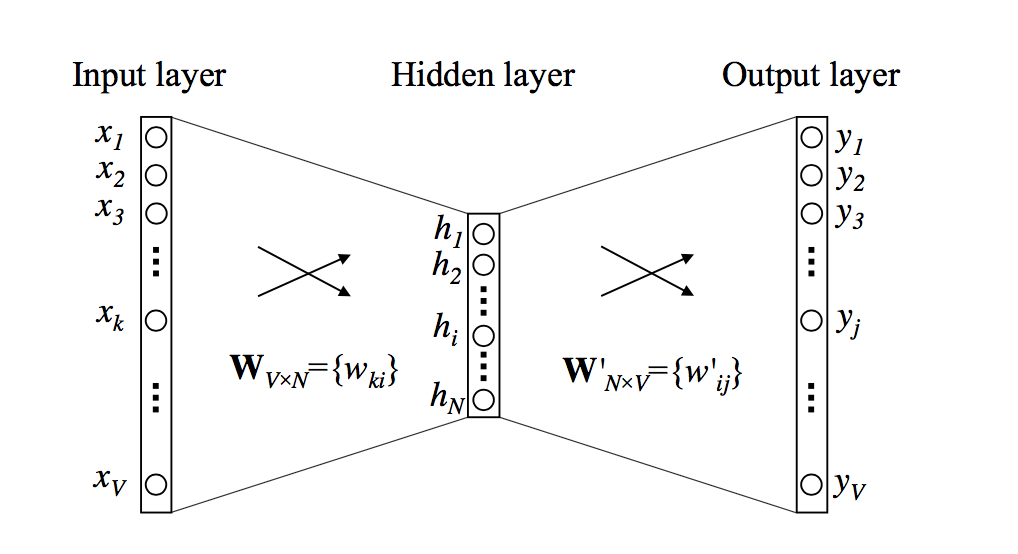
这是一个单词作为输入进行训练的情况,上图中,各参数定义如下:
- 输入层向量,\(\vec x = \{x_1,\cdots,x_V\} ^ T\) ,表示对应单词的向量表示,其初始输入一般为对应单词的one-hot编码
- 输出层向量,\(\vec y = \{y_1,\cdots,y_V\} ^ T\) ,表示对应单词的出现概率,其真实标签向量一般为对应单词的one-hot编码
- 隐藏层向量,\(\vec h = \{h_1,\cdots,h_N\} ^ T\),该层一般为一个全连接层。在这里会有点特殊,由于输入是一个one-hot编码,在之前的笔记中也已经介绍过,one-hot编码其实就是一个索引的过程,所以第 \(i\) 个单词 \(\vec x_i\) 作为输入得到的 \(\vec h\) 就是 \(W_i\) ,即 \(\vec h=W_i\),为了方便表示,下面的推导中,涉及到当前第 \(i\) 个单词的权值 \(W_i\) 更新时,会以 $h $ 代替
- 层与层之间的连接矩阵 \(W_{V \times N}\) 和 \(W'_{N \times V}\),使得 \(\vec h = W^T \vec x\) 及 $ y = \(,其中,\)u_j = W'^{(j)} h$
一般采用交叉熵作为损失函数,即 \[ L(\vec x) = - \log \vec{y} \] 代价函数取整体误差之和,设语料库为 \(D\),则 \[ J = \sum_{\vec x \in D} L(\vec x) \]
对于后面参数更新的部分,传统的是使用后向算法进行迭代更新,这里不打算进行详细推导,因为一来这部分内容会在后面开一个专题进行提及,二来进行softmax归一化的时候运算量很大,word2vec算法使用了其他的训练策略替换了后向算法。
一般来说,预训练模型都要解决两个问题:训练目标的构建和训练策略的应用。
- 训练目标的构建。由于预训练模型的训练集都是无标签的,无法像一般的分类模型一样,直接使用其自带的标签类别作为分类目标。目前预训练模型基本都是通过某些规则提取序列中的一个或多个元素作为训练目标,从而使得预训练模型可以像分类模型一样正常训练。word2vec则分为CBOW(continuous bag-of-word)和Skip-gram两种预训练语言模型。
- 训练策略的应用。一般来说,为了能学到丰富的知识,预训练任务的数据集都是非常庞大,一般很难直接进行训练,所以都会采取一些学习策略,来缓解训练的难度。word2vec则采用Hierarchical Softmax和Negative Sampling两种学习策略。
语言模型和训练策略两两组合,一共可以组合出4种不一样的模型。
一般来说,CBOW对小型数据库比较合适,而Skip-Gram在大型语料中表现更好。
2.2. 语言模型
2.2.1. CBOW
CBOW算法的基本思想是通过上下文来预测当前值(我一般简单理解为all for one),即设定一个滑动窗口,输入当前词附近一个滑动窗口大小 \(C\) 范围内的单词的特征编码,输出当前词出现概率。
注意,由于是通过上下文来预测当前值,所以只需将当前单词的上下文信息输入到输入层即可,当前的单词信息是不用输入到输入层中的,否则就会出现标签泄漏的问题,例如,带训练的单词序列,“我爱你”,当前待更新的单词为“爱”,则将“我”和“你”输入进网络即可,最终网络更新的是上下文(即“我”和“你”)的输入权值
下面给出其模型框架
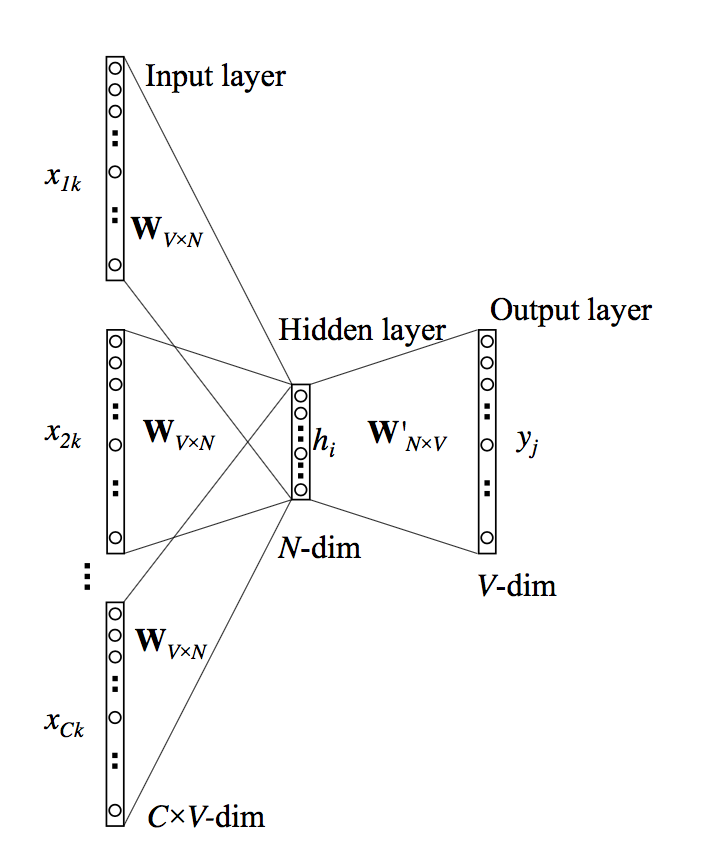
上图中,由于参数矩阵 \(W\) 是共享的,所以每次仍然只输入一个 \(\vec x\) ,且一般取窗口内的所有单词编码的均值作为输入,即 \(\vec x = \frac{1}{C}(\vec x_1 + \dots + \vec x_C)\)
后序的计算和参数的更新和普通神经网络是类似的。
2.2.2. Skip-gram(SG)
Skip-gram的思想和CBOW相反,其通过当前词来预测上下文(我一般简单理解为one for all),同样的,设定一个滑动窗口,输入当前词的特征编码,输出当前词附近一个滑动窗口大小 \(C\) 范围内的单词的输出概率。
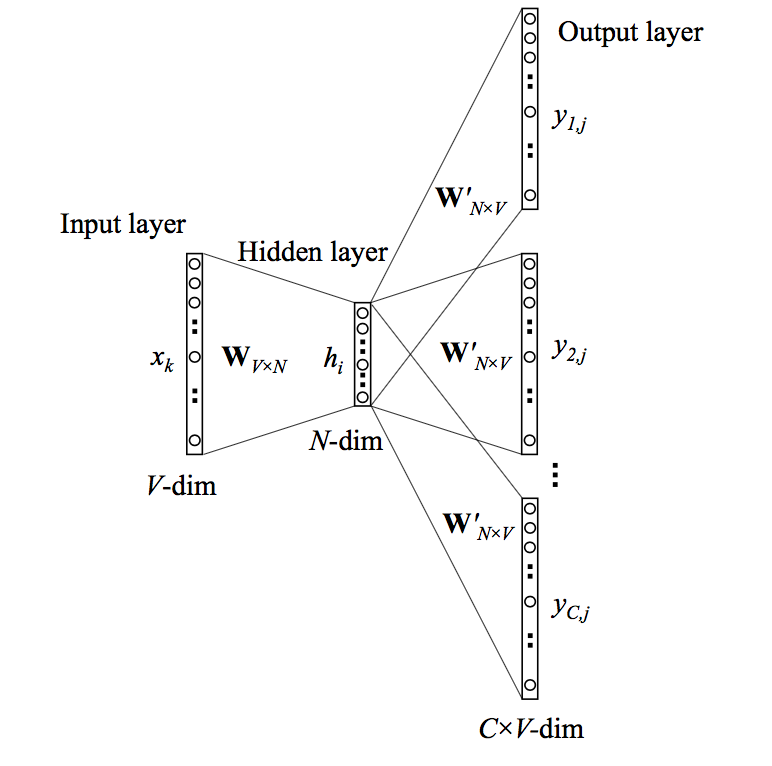
上图中,输出权值 \(W'\) 的共享的,所以,\(\vec y = \vec y_1 = \dots = \vec y_C\) ,这就意味着滑动窗口内的单词的输出概率都是一样的,即该算法认为,窗口内的单词与当前词是等概率出现的。
尽管窗口内每个单词的预测概率的一样的,但每个单词的对应的标签是不一样的,所以每个单词的误差计算也是不一样的。故更新每个单词的权值时,需要进行 \(C\) 次更新,并且计算误差的时候,需要计算的是窗口内单词序列的联合概率分布。
2.3. 优化策略
由于softmax函数要计算所有可能出现的情况,但实际上,每次更新中,绝大多数的可能出现的情况对参数更新并没有太大的帮助,所以word2vec中的优化方向都是如何减少计算所有可能出现的情况。
2.3.1. Hierarchical Softmax(HS)
这种优化的思想是通过构建哈夫曼树,只计算关键路径上对当前参数更新影响较大的节点,从而减小算法的整体时间复杂度,该算法的时间复杂度为 \(O(\log V)\)
2.3.1.1. 构建哈夫曼树
以值为单词文本,权值为词的出现概率(或者词频)作为点集构建一棵哈夫曼树,其构建的哈夫曼树如下:
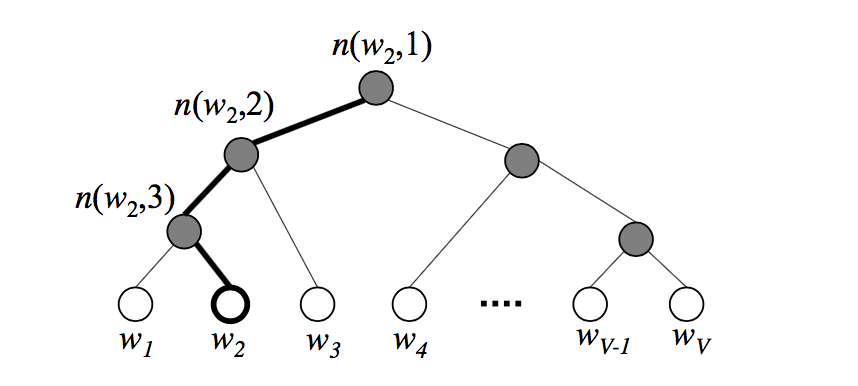
这里需要注意的是,构建哈夫曼树时使用的初始权值是词的真实概率,但在训练的是时候,每个节点的权值会重新用一个带未知参数的变量来赋值。
设当前节点的哈夫曼编码为 \(d_j^w \in \{0, 1\}\),其中,\(j\) 为当前节点的编号,设左节点则编号为0,为正类节点,右节点编号为1,为负类节点,则当前节点的选取概率为 \[ p_j^w = \left \{ \begin{array}{ll} \sigma(\vec v_j^w \cdot \vec h) & ,d_j^w = 1 \\ 1-\sigma(\vec v_j^w \cdot \vec h) = \sigma(- \vec v_j^w \cdot \vec h) & ,d_j^w = 0 \end{array} \right . \] 其中,\(\sigma(x)\) 为sigmoid函数,即 \(\sigma(x) = \frac{1}{1+e^x}\),\(\vec v_j^w\) 是当前节点的向量,是一个待训练值
其实就把上面的函数理解为激活函数即可,不使用信号函数 \(sign()\) 是因为该函数正负标签交界处跨度太大,不够平滑。
另外,不一定是要将左节点归为正类,右节点归为负类,也可以相反。
最终当前节点的输出概率为路径上所有节点的选取概率的乘积,设 \(N(w)\) 为从根节点到当前节点 \(w\) 的非叶子结点的点集,得 \[ p(w) = \prod_{j\in N} p_j^w \] 可以用数学归纳法证明,上述操作仍然会使得父节点的权值为左右节点的权值之和,根节点的权值仍然为1
特别地,非叶子节点的向量只作为辅助向量,不作为结果输出
2.3.1.2. 参数更新
上式中,待更新的参数为 \(\vec v_j^w\) 和 \(\vec h\)
将 \(p_j^w\) 表达式写成整体表达式,代入代价函数中,得 \[ J = -\sum_{\vec x \in D} \log \prod_{j\in N} \left [ \sigma(\vec v_j^w \cdot \vec h)^{1-d_j^w} \cdot \sigma(-\vec v_j^w \cdot \vec h)^{d_j^w} \right ] \\ = -\sum_{\vec x \in D} \sum_{j\in N} [(1-d_j^w) \cdot \log \sigma(\vec v_j^w \cdot \vec h)+ d_j^w \cdot \log \sigma(-\vec v_j^w \cdot \vec h)] \]
将上式中括号中的部分定义为 \(J(w,j)\),省略推导过程,直接给出如下求导结果 \[ \delta_{v_j^w} = \frac{\partial J(w,j) }{\partial \vec v_j^w } = [1-d_j^w-\sigma(\vec v_j^w \cdot \vec h)] \times \vec h \]
\[ \delta_{h} = \frac{\partial J(w,j) }{\partial \vec h } = [1-d_j^w-\sigma(\vec v_j^w \cdot \vec h)] \times v_j^w \]
每个非叶子节点 \(v_j^w\) 的参数更新 \[ \vec v_j^w \leftarrow \vec v_j^w + \eta \delta_{v_j^w} \] 最终CBOW模型 $h $ 的更新 \[ \vec h \leftarrow \vec h + \frac{\eta}{C}\sum_{j\in N} \delta_{h,j} \] 最终SG模型 $h $ 的更新 \[ \vec h \leftarrow \vec h - \eta \sum_C \sum_{j\in N} \delta_{h,j} \]
2.3.2. Negative Sampling(NS)
2.3.2.1. 构建unigram表
在网络输出层,我们将真实的输出单词对应的输出单元作为正样本,其它所有单词对应的输出单元为负样本,每次参数更新都要计算一遍全量的负样本,所以这种优化方法的思想每次参数更新,随机采取部分负样本来模拟真实分布(即本质上是一个带权采集的问题),以减少计算量。
其采样公式为: \[ P_{n}(w)=\frac{f(w)^{3 / 4}}{\sum_{w^{\prime} \neq j^{*}} f\left(w^{\prime}\right)^{3 / 4}} \] 其中, \(f(w)\) 为单词在语料库中出现的概率,分母仅考虑负向单元(不考虑正向单元),原作者建议取5~10个负向样本;\(P_{n}(w)\) 为单词被采样到的概率。
为了加快随机抽取的速度,原作者设计一个unigram(应该翻译成一元标注?)表,原理很简单,即开创一个内存为 \(M\) 的空间(原作者取 \(M=10^8\),其实可以直接取语料集单词的总数),每个单词 \(w\) 占据 \(MP_n(w)\) 个内存空间,最后取一个在区间 \([0,M]\) 内的随机整数,该整数对应的内存空间上的单词即为抽取的负样本。
2.3.2.2. 参数更新
参数部分其实和未优化前的word2vec模型的参数更新是差不多的,实质上就是将softmax计算中的语料库中所有的单词集合 \(D\) 换成随机抽取的样本集 \(D'\),下面不加推导地给出各参数更新的最终公式
定义单词标签 \(L(w) \in \{0, 1\}\),则代价函数 \[ J = -\sum_{j=0}^V \sum_{w\in D'} [(1-L(w)) \cdot \log \sigma(-\vec W'^{(j)} \cdot \vec h)+ L(w) \cdot \log \sigma(\vec W'^{(j)} \cdot \vec h)] \] 将上式中括号中的部分定义为 \(J(W'^{(j)},w)\),\(W'^{(j)}\) 的梯度计算及更新为 \[ \delta_{W'^{(j)}} = \frac{\partial J(\vec W',w) }{\partial W'^{(j)} } = [L(w)-\sigma(W'^{(j)} \cdot \vec h)] \times \vec h \]
\[ W'^{(j)} \leftarrow W'^{(j)} + \eta \delta_{W'^{(j)}} \]
\(\vec h\) 的梯度计算为 \[ \delta_{\vec h} = \frac{J(W'^{(j)},w)}{\partial \vec h } = [L(w)-\sigma(W'^{(j)} \cdot \vec h)] \times \vec W'^{(j)} \] 参数更新
CBOW模型 \[ \vec h \leftarrow \vec h + \frac{\eta}{C} \delta_{\vec h} \] SG模型 \[ \vec h \leftarrow \vec h + \eta \delta_{\vec h} \]
3. 代码实现的一些trick
3.1. \(\sigma(x)\) 的近似计算
在HS算法中,由于sigmoid函数计算最为频繁使用,所以word2vec作者(下面称其为原作者)对这一部进行了优化。
中将 \([-6,6]\) 区间内分成k等分,每个区间用 \(x_k = -6 + k/K\) 表示,分别计算每个区间的 \(\sigma(x_k)\) 值,并保存为一张表,计算的时候查表即可,即 \[ \sigma(x) = \left \{ \begin{array}{ll} 0 & ,x \leq -6 \\ \sigma(x_k) & ,x \in (-6, 6) \\ 1 & , x \geq 6 \end{array} \right . \] 不妨来看 \(e^z\) 的泰勒展开 \[ e^{z}=1+\frac{z}{1 !}+\frac{z^{2}}{2 !}+\frac{z^{3}}{3 !}+\ldots \] 所以当 \(z\) 较小(\(|z|<1\))时,取前n项可以用于近似计算,所以 \(\sigma(x)\) 总体的损失的精度是较小的,但能极大的提高运算速度。
3.2. 低频词处理
原作者直接将词频低于阈值(默认为5)的单词从词典中删掉,但这种方法过于粗暴,可以加入一个限制条件,只有当语料库大小 \(|D|\) 和词典大小 \(n\) 满足 \(0.7|D| > n\) 才进行低频词处理
3.3. 高频词处理
语料库中出现频率最高的往往都是停用词,这些词能提供的信息很少,但训练时消耗的资源占比却很大,原作者采用 subsampling 的技巧,通过设立一个词频阈值 \(t\) ,将词 \(w\) 以 \[ P_n(w)=1-\sqrt{\frac{t}{f(w)}} \] 的概率舍弃,其中 \(f(w)\) 为该单词出现的概率
而原作者源码中采用的公式为 \[ P_n(w)=1-\left(\sqrt{\frac{t}{f(w)}}+\frac{t}{f(w)}\right) \]
3.4. 随机窗口
原始操作中,设窗口大小为 \(C\) ,取前后各 \(2/C\) 个单词进行训练,但为了防止过拟合,设随机整数 \(R \in [0,C]\),每次取窗口训练时,取前 \(l=R\) 个单词及后 \(r=C-R\) 个单词进行训练。
特别地,对于上下文单词数 \(l'<R\) 或 \(r' < C-R\) 时,则取 \(l=l'\) 或 \(r=r'\)
3.5. 自适应学习率
原作者加入了自适应的学习率,使得我们前期可以设立一个较大的学习率进行训练,加快训练速度
更加具体的,没训练10000(非固定值,可根据自身经验修改)个单词,设已经处理过的单词数为n,则对学习率进行如下调整 \[ \eta \leftarrow \eta (1 - \frac{n}{|D| + 1}) \] 为了不使得学习率过小,原作者还设立了一个最低阈值 \(\eta_{min} = 10^{-4}\)
3.6. 并行训练
为了加快速度,原作者采用了并行训练的方法,但由于权值都是共用的,所以会出现两个线程同时更新一个单词的权值的情况,但原作者认为,一般训练的词表都会很大,所以同时取到同一个单词的概率很小,即使偶然取到了,对权值更新的影响很低,所以这种情况可以忽略(大佬就是大佬,果然不拘小节-_-||)
4. references
https://www.bookstack.cn/read/huaxiaozhuan-ai/spilt.3.142adbd00f395138.md#7ko7d2
word2vec原理(一) CBOW与Skip-Gram模型基础
http://www.hankcs.com/nlp/word2vec.html
Word2Vec Tutorial - The Skip-Gram Model
[word2vec代码注释 - @太极儒](https://blog.csdn.net/cnki_ok/article/details/41719401)
Word2vec神经网络详细分析--TrainModelThread分析_老笨妞-CSDN博客_word2vec 神经网络