1. DDIM

ICLR 2021年的论文：Denoising Diffusion Implicit Models

代码实现：

官方基于pytorch的实现代码
个人基于pytorch的实现代码

原始的ddpm模型运行速度慢的一个重要原因是，其扩散过程是基于马尔科夫链推导出来的，即基于假设 \(\mathbf x_t = q\left(\mathbf x_t \mid \mathbf x_{t-1}\right)\) ，推导出 \[ p_{\theta}(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \propto q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \propto \mathcal{N}(\mathbf{x}_{t-1}; {\tilde{\boldsymbol{\mu}}}(\mathbf{x}_t, \mathbf{x}_0), {\tilde{\beta}_t} \mathbf{I}) \] 这意味着无论是正向还是逆向都需要对所有时刻都进行采样。

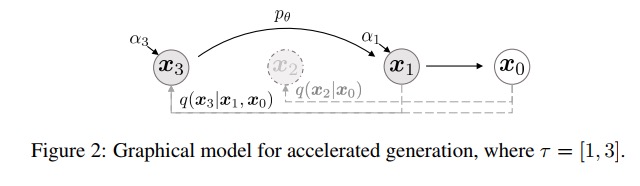
但可以注意到，在ddpm推导出最终的结论的过程中，其实仅依赖了 \(q\left(\mathbf x_t \mid \mathbf x_0\right)\) 条件，而并没用到 \(q\left(\mathbf x_t \mid \mathbf x_{t-1}\right)\) 这个条件。所以ddim发现可以绕开马尔科夫链的限制，改为跳步的采样。通过减少采样的timestep，来加速运行速度。

但由于没了 \(q\left(\mathbf x_t \mid \mathbf x_{t-1}\right)\) 这一前提，所以需要另辟蹊径对一些表达式进行重新推导。

根据ddpm的推理，有 \[ q\left(\mathbf x_t \mid \mathbf x_0\right)=\mathcal{N}\left(\mathbf x_t ; \sqrt{\bar{\alpha}_t} \mathbf x_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right) \\ q\left(\mathbf x_{t-1} \mid \mathbf x_0\right) = \int_{\mathbf x_t} p\left(\mathbf x_{t-1} \mid \mathbf x_t, \mathbf x_0\right) q\left(\mathbf x_t \mid \mathbf x_0\right) d \mathbf x_t \\ q\left(\mathbf x_1 \mid \mathbf x_0\right)=\mathcal{N}\left(\mathbf x_1 ; \sqrt{\bar{\alpha}_1} \mathbf x_0,\left(1-\bar{\alpha}_1\right) \mathbf{I}\right) \] 可以观察到，上式中存在所需表达式 \(p\left(\mathbf x_{t-1} \mid \mathbf x_t, \mathbf x_0\right)\)。

不妨假设 \(q\left(\mathbf x_1 \mid \mathbf x_0\right)\) 和 \(q\left(\mathbf x_t \mid \mathbf x_0\right)\) 依然成立，且 \(\mathbf x_{t-1}\) 是 \(\mathbf x_0\) 和 \(\mathbf x_t\) 的线性组合，及 \(p\left(\mathbf x_{t-1} \mid \mathbf x_t, \mathbf x_0\right)\) 服从高斯分布。于是有 \[ p\left(\mathbf x_{t-1} \mid \mathbf x_t, \mathbf x_0\right)=\mathcal{N}\left(\mathbf x_{t-1} ; \lambda \mathbf x_0+k \mathbf x_t, \sigma_t^2 \mathbf{I}\right) \] 假设高斯噪声 \(\epsilon_{t-1}^{\prime} \sim \mathcal N(0, \mathbf I)\) ，使用重参数技巧，上述的高斯分布形式可以改写为

\[ \mathbf x_{t-1}=\lambda \mathbf x_0+k \mathbf x_t+\sigma \boldsymbol\epsilon_{t-1}^{\prime} \\ \mathbf x_t=\sqrt{\bar{\alpha}_t} \mathbf x_0+\sqrt{\left(1-\bar{\alpha}_t\right)} \boldsymbol\epsilon_t^{\prime} \]

两式合并，可得 \[ \begin{aligned} \mathbf x_{t-1} & =\lambda \mathbf x_0+k\left(\sqrt{\bar{\alpha}_t} \mathbf x_0+\sqrt{\left(1-\bar{\alpha}_t\right)} \boldsymbol{\epsilon}_t^{\prime}\right)+\sigma_t \boldsymbol{\epsilon}_{t-1}^{\prime} \\ & =\left(\lambda+k \sqrt{\bar{\alpha_t}} \right) \mathbf x_0+k \sqrt{\left(1-\bar{\alpha}_t\right)} \boldsymbol{\epsilon}_t^{\prime}+\sigma_t \boldsymbol{\epsilon}_{t-1}^{\prime} \\ & = \left(\lambda+k \sqrt{\bar{\alpha_t}} \right) \mathbf x_0 + \sqrt{\left(k^2\left(1-\bar{\alpha}_t\right)+\sigma_t^2\right)} {\boldsymbol{\epsilon}}_{t-1} \end{aligned} \]

注：上式最后一步的推导使用了高斯分布的可加性。

又 \[ \mathbf x_{t-1}=\sqrt{\bar{\alpha}_{t-1}} \mathbf x_0+\sqrt{\left(1-\bar{\alpha}_{t-1}\right)} \boldsymbol\epsilon_{t-1} \]

联合解方程，并统一符号后可得 \[ \mathbf{x}_{t-1}=\sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0 +\sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2} \cdot \bar{\boldsymbol{\epsilon}}_t+\sigma_t \boldsymbol\epsilon_t \] 其中， - \(\mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \bar{\boldsymbol{\epsilon}}_t)\) 论文中称为预测的 \(\mathbf x_0\) - \(\sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2} \cdot \bar{\boldsymbol{\epsilon}}_t\) 论文中称为 \(\mathbf x_0\) 的方向 - \(\sigma_t\) 是一个超参数。当 \(\sigma_t=\sqrt{\left(1-\bar{\alpha}_{t-1}\right) /\left(1-\bar{\alpha}_t\right)} \sqrt{1-\bar{\alpha}_t / \bar{\alpha}_{t-1}}\) 时，生成过程与DDPM一致；当 \(\sigma_t=0\) 时，随机噪声项为0，采样过程是确定的，此时的生成模型是一个隐概率模型(implicit probabilstic model)，此时diffusion model称之为denoising diffusion implicit model（DDIM）。该值一般由一个 \(\eta \in [0,1]\) 的超参数控制

现在回到先回到一开始的假设，假设部分其实还没有证明。论文中通过重新构造 \(q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)\) 的表达形式，证明了一开始的假设是成立的，且ddim具有和ddpm相同的损失函数，具体证明可见原论文的附录部分。

这意味着，\(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)\) 部分不需要重新推导了，正向阶段，仍然使用ddpm，在长度为 \(T\) 的时间序列 \([1,...,T]\) 中，训练得到一个模型；逆向阶段，使用ddim，从原时间序列中采样出一个长度为 \(S\) 的时间子序列 \([\tau_1,...,\tau_S]\)，进行推理预测。对于时间步的采样，一般采用线性或平方的采样，即 \(\tau = \{\lfloor k t_i \rfloor \}\) 或 \(\tau = \{\lfloor k t_i^2 \rfloor \}\)

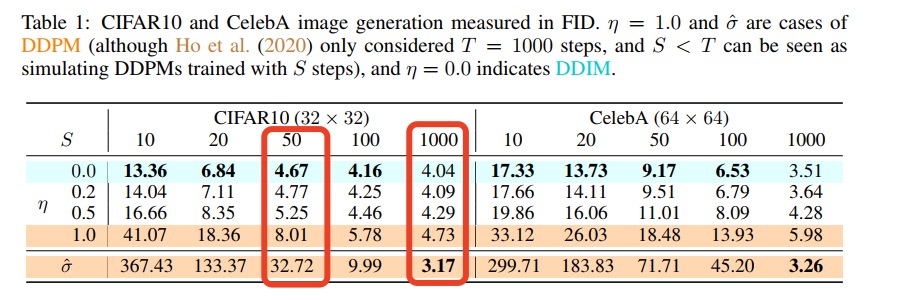
最后，论文中还通过实验发现，在CIFAR10数据集上，仅采样50步，即可达到ddpm中采样1000步的90%的效果。

2. LDM

CVPR 2022年的论文：High-Resolution Image Synthesis with Latent Diffusion Models

代码实现：

官方基于pytorch的的实现代码
个人基于pytorch的实现代码

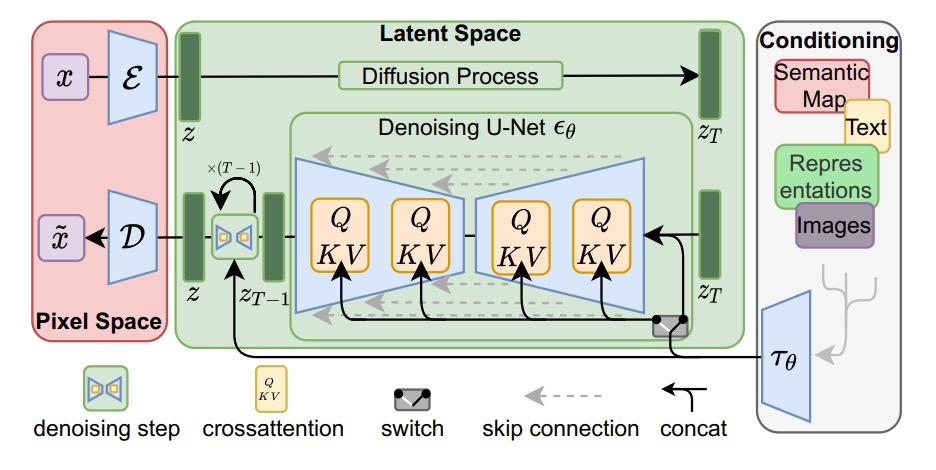
网络结构：

2.1. 两段式训练

在训练高分辨率的图片时，往往需要把模型设计得很深，这导致模型的权重变得很大，以至于难以拟合。这消耗了大量的空间即训练时间。

ldm的想法也很简单，既然一次性训练很困难，那么就分成两个模型，依次进行训练，降低训练的难度，即所谓的二段式训练。

论文设计了一个VAE模型，中间包了一个diffusion模型（可以想象成两片汉堡中间夹住了一片芝士）。其中，VAE负责语义的压缩和转化，diffusion负责风格的控制。

注：由于VAE模型是基于似然的方法更强调良好的密度估计，更容易优化，所以选择了VAE作为图片的生成器。而GAN虽然非常难优化，但可以生成高质量的图像，为了避免潜在的高方差空间，论文在训练VAE模型的时候，还加入GAN loss，所以在训练VAE的同时，还需要训练一个GAN模型作为辅助模型，可谓是集众多生成模型于一身。

整体的训练流程为：先训练出一个VAE模型；然后diffusion模型再接入刚刚训练好的VAE的解码器，进行diffusion的训练。

2.2. 条件控制生成

既然现在diffusion模型拟合的是中间的隐变量，那么就很容易添加一些额外条件控制，用来指导图片的生成。于是由此衍生出文生图和图生图两种目前主流的图片生成模式。

文生图。需要提供一个文本，即提示词。将提示词输入进一个语言模型（原始的LDM使用的是bert模型）中，得到一个文本表达的矩阵向量。将其作为attention的kv对，由此便可以将图片的表达向量，投影成文本的表达向量，以此控制图片的风格、性状、内容。
图生图。需要提供一个文本和图片，提示词的处理和上面的流程一样。将图片输入进VAE的编码器中，得到一个图片的语义压缩向量，将其看做是 \(x_{t-1}\) ，再做一个前向采样，便得到 \(x_t\) ，然后在此基础上进行逆向采样。以此便使最终生成的图片仍能保留原有图片的部分特征。