算法基础数据结构

算法基础

发布日期: 2020-07-07

更新日期: 2022-08-10

文章字数: 2k

阅读时长: 7 分

阅读次数:

本篇用到的代码传送门

1. 树的基本术语

节点的度

节点拥有子树的数量
树的度

树内各节点的度的最大值，是一个横向的量。
节点的深度

节点从上到下的最大层数，是一种纵向的量。根节点的深度为1
节点的高度

节点从下到上的最大层数，是一种纵向的量。叶子节点的高度为1
叶子节点

度为0的节点
有序树

各子树不能互换，否则为无序树
森林

m棵互不相交的树的集合

2. 二叉树的性质

二叉树（Binary Tree）是使用最多的树结构。

二叉树是无序树
一般地，默认二叉树上每个节点的值都不相同
二叉树的第 \(i\) 层上至多有 \(2^{i-1}\) 个节点
深度为 \(k\) 的二叉树至多有 \(2^k -1\) 个节点
如果叶子节点数为 \(n_0\)，度为2的节点数为 \(n_2\)，则 \(n_0=n_2+1\)
深度为 \(k\) 且含有 \(2^k -1\) 个节点（即每一层节点树都是最大的）的树为满二叉树
深度为 \(k\)，有 \(n\) 个节点的二叉树，当且仅当每个节点都与深度为 \(k\) 的满二叉树中编号从1到 \(n\) 的节点一一对应时（定义真拗口-_-||，其实就是除最后一层外，其他层都是满的，最后一层从左到右是满的），称为完全二叉树
除最后一层外，其他层都是满的，称为理想平衡二叉树
满二叉树 \(\subseteq\) 完全二叉树 \(\subseteq\) 理想平衡二叉树
具有 \(n\) 个节点的完全二叉树的深度为 \(\lfloor \log_2 n \rfloor + 1\)

3. 二叉树的存储结构

3.1. 顺序表

依次自上而下、自坐往右存储节点的元素，中间遇到空节点用自定义的符号（例如 null，# 等）占位即可。

如果以数组索引为 \(1\) 作为二叉树的根节点，设当前节点在数组的索引为 \(i\) ，那么，其左子树的索引为 \(2i\)，右子树的索引为 \(2i+1\)

3.2. 链表

每个节点有3份内存空间——数据、左指针和右指针。

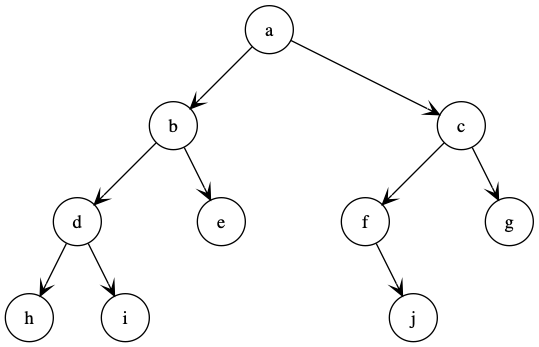
4. 二叉树的可视化

4.1. 图像形式

可以使用graphviz对二叉树进行图像可视化，但原生态的graphviz做出来的图并不好看，所以网上有大神写了一个优化的脚本。

把优化脚本保存为 binarytree.gvpr，然后把下面绘图语句保存为 binarytree.dot

digraph G {
    node [shape=circle]
    edge [arrowhead=vee]
    a -> b
    a -> c
    b -> d
    b -> e
    c -> f
    c -> g
    d -> h
    d -> i
    _f[style=invis]
    f -> _f[style=invis]
    f -> j
}

当只有一个节点时，会默认将其作为右子树，所以需要一个占位节点将其挤到左子树那边。上述语句中，[style=invis] 表示隐藏属性，_f 就是一个隐藏的占位节点。

最后命令行中输入下面的命令

dot tree.dot | gvpr -c -f binarytree.gvpr | neato -n -Tpng -o binarytree.png

附：一些常用的布局参数如下

dot ：默认布局方式，主要用于有向图

neato ：主要用于无向图

twopi ：主要用于径向布局

circo ：圆环布局

fdp ：主要用于无向图

sfdp ：主要绘制较大的无向图

patchwork ：主要用于树哈希图（tree map）

即可得到

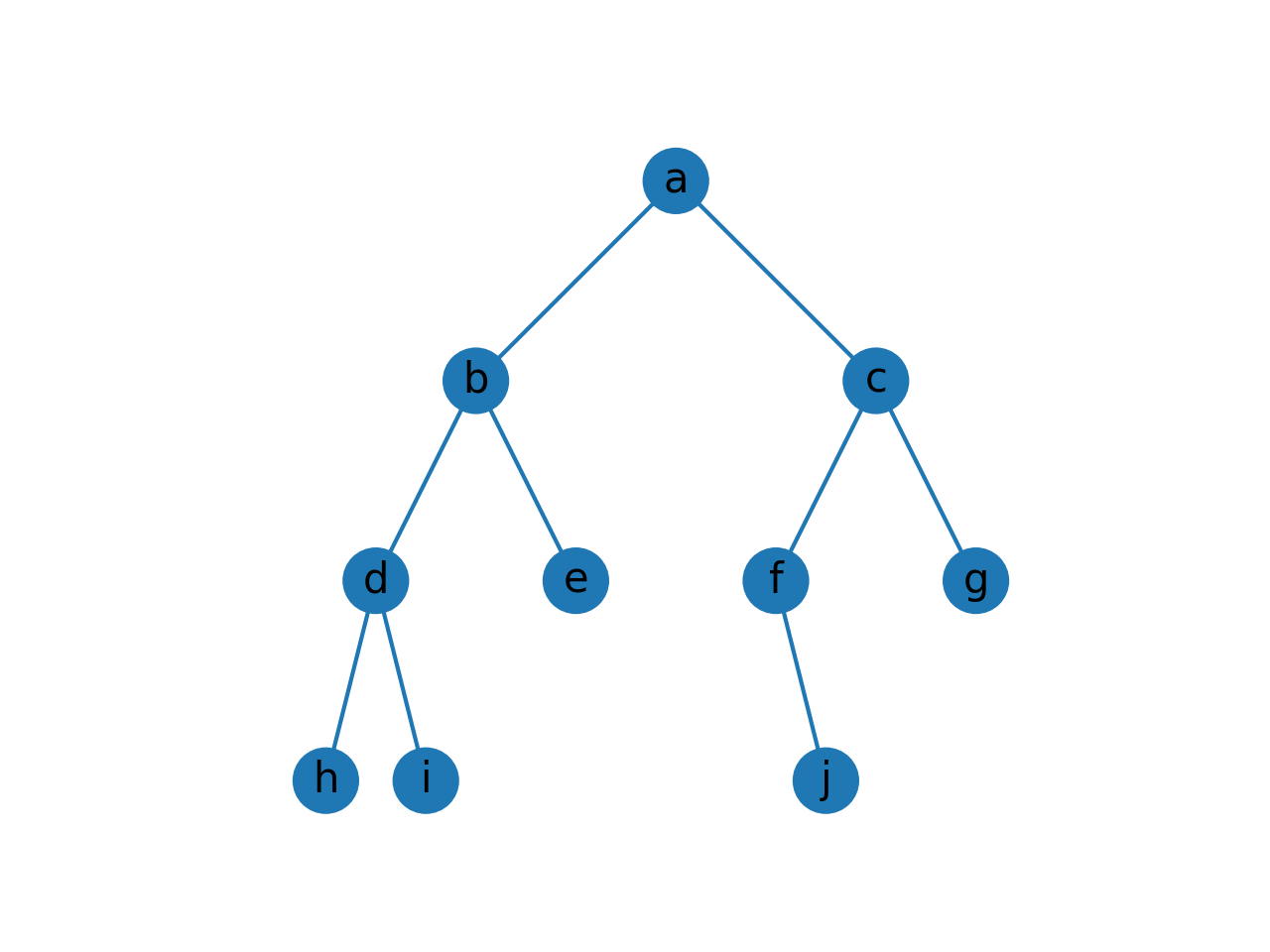
当然图像可视化怎么少得了信仰的matplotlib呢😝

实现代码，下面是实现效果图：

4.2. 文本形式

顺序表形式: [None, 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', None, None, None, 'j']
广义表形式: a(b(d(h,i),e),c(f(,j),g))
树形结构形式:
a-->b-->d-->h
        └-->i
    └-->e
└-->c-->f
        └-->j
    └-->g

5. 二叉树的遍历

实现代码

5.1. 深度优先（Depth-First Search, DFS）

5.1.1. 中序遍历（lDR）

即 左->根->右

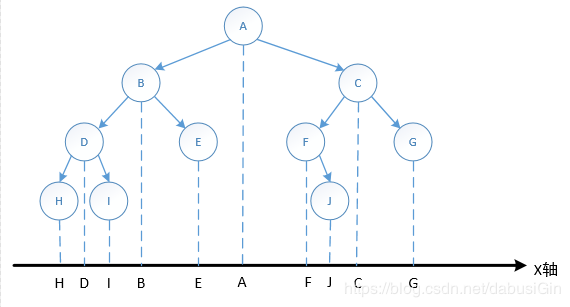
中序遍历是最符合人的运算逻辑的，例如，四则运算 1+2-3 就是中序遍历的结果，所以多被用于运算的树形结构可视化。

中序遍历可以从树形结构直接看出来，只要把二叉树往下压扁，就可以得到其中序遍历了，如下图所示

5.1.2. 后序遍历（LRD）

即 左->右->根

后序遍历是最符合计算机的阅读逻辑的，例如，上面四则运算的后序遍历结果为 12+3-

在前面循环与递归一文中也提到，后序遍历是逆波兰式，所以这种遍历是计算机应用最多的遍历，凡是涉及递归的地方，都有后序遍历的身影。

5.1.3. 先序遍历（DLR）

即 根->左->右 ，

先序遍历是比较符合人的阅读逻辑的，例如，上面四则运算的后序遍历结果为 -+123

先序遍历就是波兰式，可以理解为先把一条路走到黑，碰壁后再回到上一个分岔路，然后把另一条路走到黑……最后把所有路都走完，遍历就结束了。所以常用于迷宫寻路算法和文件目录的输出

5.1.4. 从遍历序列还原二叉树

实现代码

首先，可以确定二叉树的条件为 中序 & (先序 | 后序)，所以，中序是必须要给定的。因为先序和后序在本质上都是将父节点与子节点进行分离，但并没有指明左子树和右子树的能力，没有中序不能确定一个二叉树。

以上面可视化例子中的二叉树作为例子，下面该二叉树的三种遍历结果：

前序遍历: ['a', 'b', 'd', 'h', 'i', 'e', 'c', 'f', 'j', 'g']
中序遍历: ['h', 'd', 'i', 'b', 'e', 'a', 'f', 'j', 'c', 'g']
后序遍历: ['h', 'i', 'd', 'e', 'b', 'j', 'f', 'g', 'c', 'a']

然后，只拿中序和先序，还原二叉树。下面给出还原的流程：

从先序按顺序从左往右读（后序为从右往左读），把第一个元素作为二叉树的根节点，并将其标记为已读元素。
从先序序列中读出下一个元素作为当前元素。
如果当前元素在中序序列中没有位于两个已读元素的中间，则在中序序列中，判断其位于最靠近已标记元素的哪一侧，如果位于左侧，则为那一个标记元素的左子树，右侧则为右子树。例如，b 位于 a 的左侧，则作为 a 的左子树。
如果当前元素在中序序列中位于两个已读元素的中间，则在中序序列中，作为左边最靠近当前元素的已标记元素的右子树（后序为右边最靠近当前元素的已标记元素的左子树），如果右子树已经存在，则作为右边元素的左子树（后序相反即可）。例如，f 位于 a 和 c 中间，本来，i 应该为 a 的右子树，但 a 的右子树已经存在了，所以只能作为 c 的左子树。
把当前元素标记为已读元素。
重复步骤2-5，直至所有元素都被标为已读元素，二叉树还原完毕。