前面说到了递归和二叉树,递归和二叉树中都提到了逆波兰式,而应用逆波兰式最典型的例子就是四则运算,所以下面介绍一下怎样实现一个四则运算计算器
项目代码传送门
1. 输入输出
>>> calculate('-1+2*(3.2+4)*5+6')
77.0下面的讲解基于上述例子。
2. 输入字段分割
我们把输入字符串分成3部分——运算符(即 +-*/)、运算值(可以是整数或者小数,暂不支持科学计数法,如果第一个字符是 -,这里将其当做负数运算值处理 )、优先级重定向符(即 ())
3. 二叉树构建
有如下规则:
- 运算符都位于非叶子节点,运算值都位于叶子节点;
- 优先级较低的运算符作为主节点,优先级较高或相同的运算符作为其子树。
所以我们有以下构建二叉树的流程
- 去除首尾多余的括号。怎样判断是否为多余的括号,其实也很简单。先把首尾的括号去掉,然后从左往右对左右括号进行遍历计数,初始计数值为0,当遇到左括号是减1,遇到右括号时加1。当计数值有出现大于1的情况时,说明首尾的括号并非多余的。例如下面这个例子的括号就不是多余的,
(1+2)*(3+4) - 从左往右遍历输入字符串。遍历的过程中,把括号括起来的内容当成一个运算值。这里,我们依然可以使用上面对括号计数的方法屏蔽掉括号里面的内容。初始计数值为0,当计数值小于0时,跳过读到的字符,只有当计数值等于0时,才处理读到的字符。特别地,当计数值大于0时,说明输入的方程的左右括号失配了。
- 遍历查找优先级最低的运算符,将其作为主节点,并把两侧作为其左右子树。又因为
+-的优先级最低,所以遇到的第一个+或-符号,即可将其作为主节点了。 - 左右子树如果是运算值,则将其转换为数值型进行存储;如果不是运算值,那么重复步骤1~4进行递归操作,直至所有的叶子节点都为运算值。
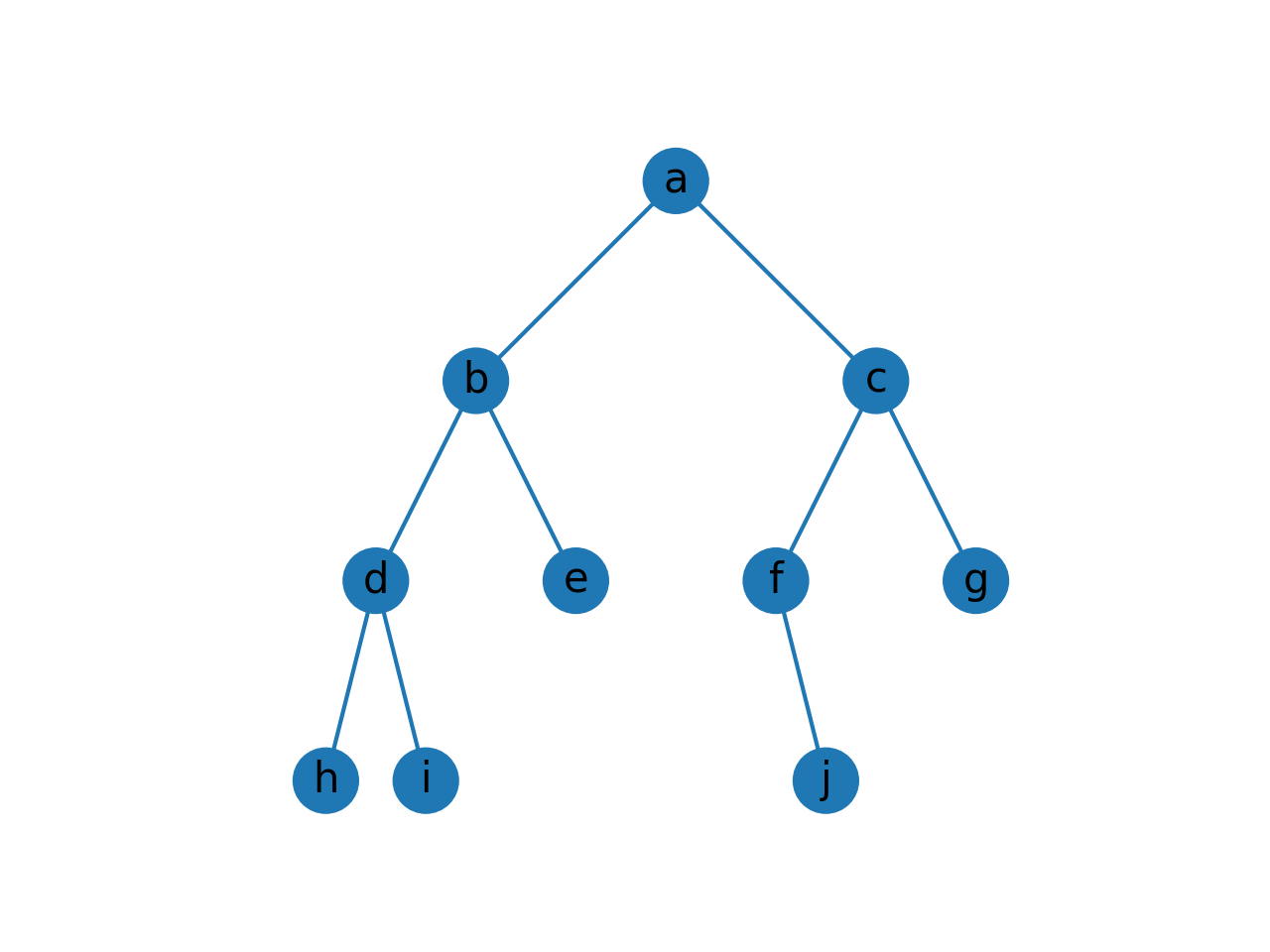
按照上述流程, -1+2*(3.2+4)*5+6 构建的二叉树如下:
4. 最终运算
最后就是逆波兰式地应用了。
对二叉树进行后序遍历,上面例子的遍历结果如下
['-1', '2', '3.2', '4', '+', '*', '5', '*', '6', '+', '+']建立一个栈,对运算值压入栈尾,如果遇到运算符,则从栈尾中弹出两个运算值,进行对应的运算,然后将运算结果压入栈尾。
遍历完后,栈内应该只存在一个数值,这个数值就是最终的结果了。
这个计算器可以扩展应用于所有的二目运算符的计算中,但因为这只是一个demo,只要简单的展示就可以了,所以就没有写这么多功能了其实是因为懒。
That's all~ Have a good time~