个人基于numpy的实现代码
个人基于pytorch的实现代码
1. 二分类
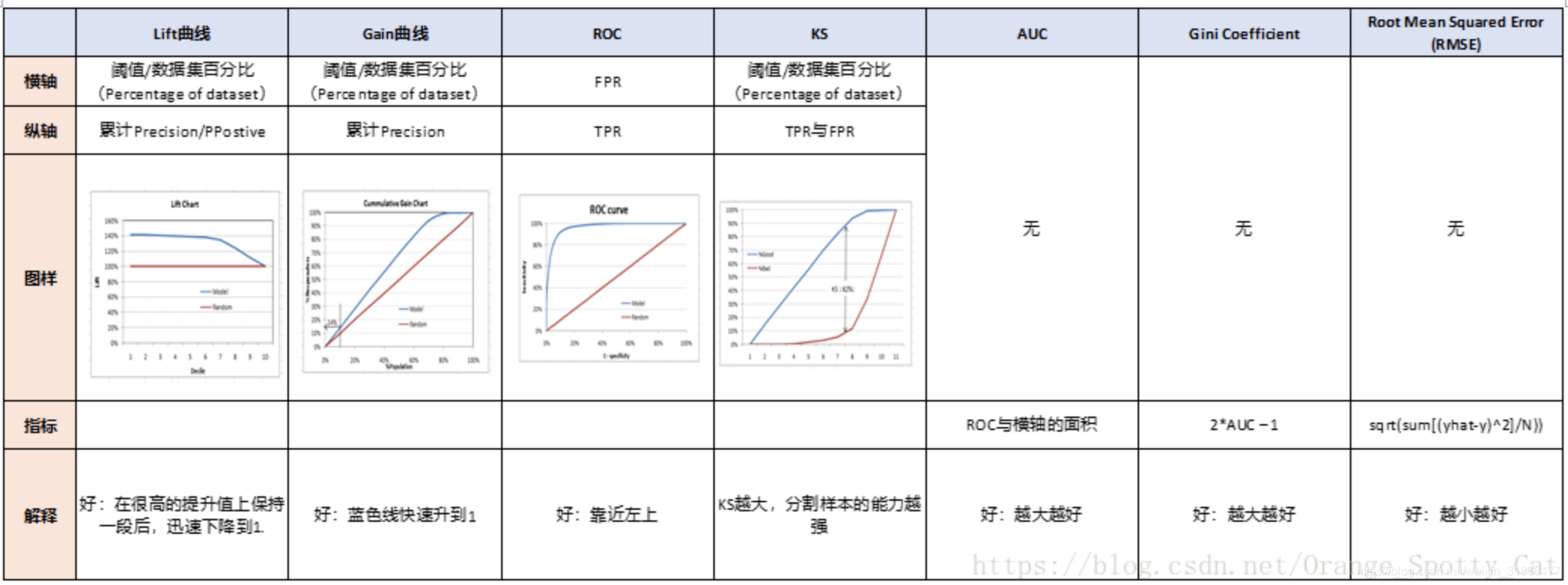
先来一张全家福
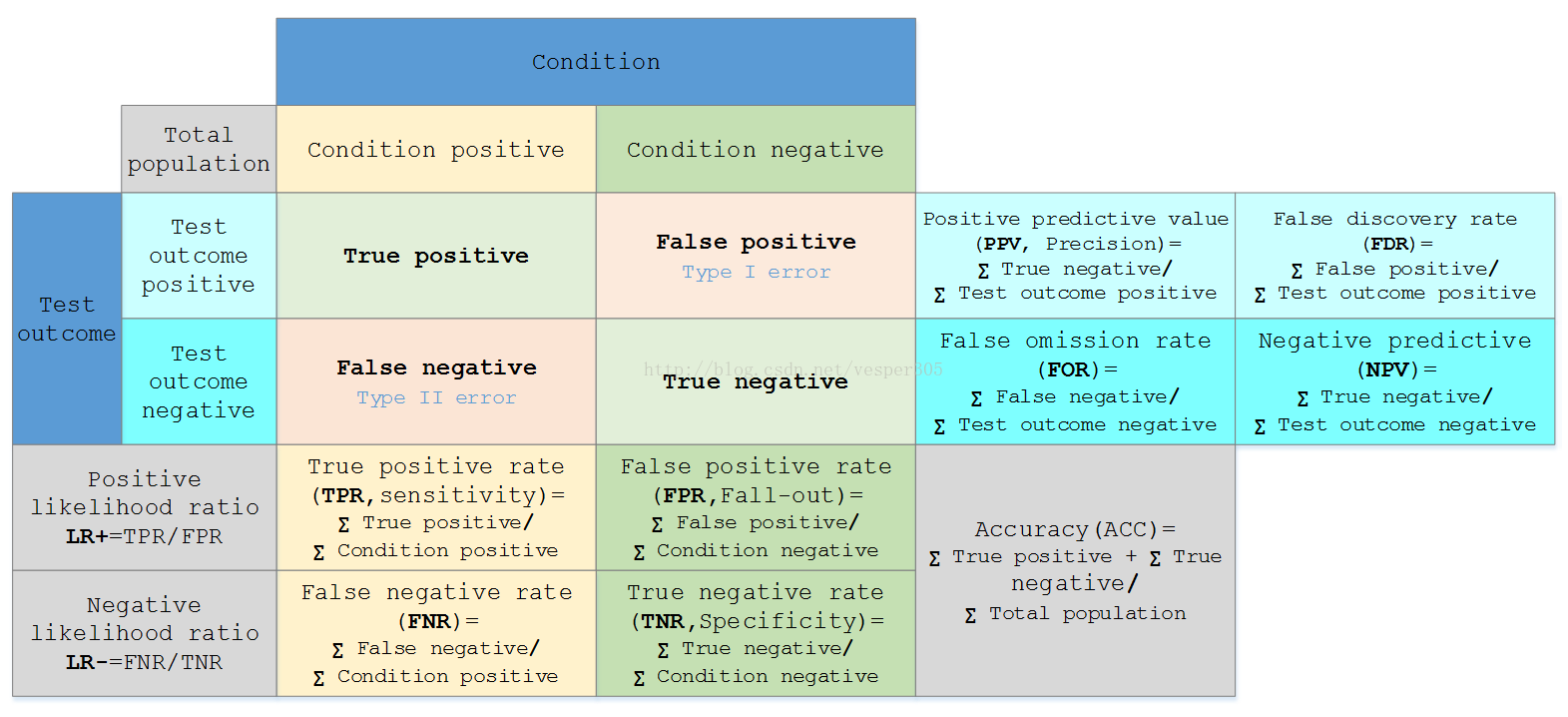
上图中,PPV一项计算错误,分子应为TP而非TN
1.1. 一级指标
一级指标是的底层的指标,只包括各种最基本的数值统计,其中的各种统计结果用一个混淆矩阵(confusion matrix)来表示
混淆矩阵是数据科学、数据分析和机器学习中总结分类模型预测结果的情形分析表,以矩阵形式将数据集中的记录按照真实的类别与分类模型作出的分类判断两个标准进行汇总。
| \(y=1\) | \(y=0\) | |
|---|---|---|
| \(f(x)=1\) | \(TP=\sum_i I(y_i=1,f_i=1)\) True Positive,真正例 |
\(FP=\sum_i I(y_i=0,f_i=1)\) False Positive,假正例 统计学上的第一类错误 |
| \(f(x)=0\) | \(FN=\sum_i I(y_i=1,f_i=0)\) False Negative,假反例 统计学上的第二类错误 |
\(TN=\sum_i I(y_i=0,f_i=0)\) True Negative,真反例 |
混淆矩阵一般使用热力图进行可视化,但由于二分类下的热力图展示并不直观,这里留在多分类的时候再进行展示。
1.2. 二级指标
二级指标是一级指标间的各种比率
| 简称 | 全称 | 别名 | 计算公式 |
|---|---|---|---|
| TPR | true positive rate | 召回率(recall)或灵敏度(sensitivity) | \(\frac{TP}{TP+FN}=\frac{\sum_i I(y_i=1,f_i=1)}{\sum_i I(y_i=1)}\) |
| FPR | false positive rate | 脱落率(fall-out) | \(\frac{FP}{FP+TN}=\frac{\sum_i I(y_i=0,f_i=1)}{\sum_iI(y_i=0)}\) |
| FNR | false negative rate | \(\frac{FN}{TP+FN}=\frac{\sum_i I(y_i=1,f_i=0)}{\sum_i I(y_i=1)}\) | |
| TNR | true negative rate | 特异度(specificity) | \(\frac{TN}{FP+TN}=\frac{\sum_i I(y_i=0,f_i=0)}{\sum_i I(y_i=0)}\) |
| PPV | positive predictive value | 精确率(precision) | \(\frac{TP}{TP+FP}=\frac{\sum_i I(y_i=1,f_i=1)}{\sum_i I(f_i=1)}\) |
| FDR | false discovery rate | \(\frac{FP}{TP+FP}=\frac{\sum_i I(y_i=0,f_i=1)}{\sum_i I(f_i=1)}\) | |
| FOR | false omission rate | \(\frac{FN}{FN+TN}=\frac{\sum_i I(y_i=1,f_i=0)}{\sum_i I(f_i=0)}\) | |
| NPV | negative predictive value | \(\frac{TN}{FN+TN}=\frac{\sum_i I(y_i=0,f_i=0)}{\sum_i I(f_i=0)}\) | |
| ACC | accuracy | 准确率 | \(\frac{TP+TN}{TP+FP+FN+TN}=\frac{\sum_i I(y_i=1,f_i=1) + \sum_i I(y_i=0,f_i=0)}{N}\) |
上表中,用的比较多的是召回率、精确率和准确率,其中
- 召回率表示真实正样本中预测正确的概率,即查全率,适合于“宁可杀错一千,不放过一个”的场合,例如预测全为正,则召回率就是1;
- 精确率表示预测为正的样本中正确的概率,即查准率,适用于“宁缺毋滥”的场合,例如预测全为负,则精确率为1;
- 准确率表示所有样本中预测正确的概率,能够在一定程度上反映算法的整体性能。
1.3. 三级指标
三级指标是二级指标之间的相互计算,三级指标除了可以对当前分类标准下模型的性能,还能帮助算法选择最好的分类阈值以及评估算法在任意分类标准下的一个综合性能。
理想情况下,正负样本的预测值服从于两个不重叠的分布。一个完美的模型可以在特定的分类阈值下,将两个分布完全区分开。但最优阈值时未知的,通常可以通过如下手段求取:
- 按照一定的步长设置阈值,计算各个阈值下的指标值,形成一个点集。点集中最大值对应的阈值便是最优阈值。
- 用直线将这些点集连接,便得到一条曲线。曲线的趋势便反应了模型的分类性能。
常用到的三级指标有以下几个
1.3.1. F-Measure
召回率和精确率两者反映的指标都是片面,之间的差别是分母中,一个为FN,一个为FP,而这两者是负相关的,所以,精确率与召回率是矛盾的,鱼与熊掌不可兼得,所以需要一个指标来综合两者,这就引出了F-Measure值,F-Measure是召回率和精确率的加权调和平均,其表达式为 \[ F_\alpha=\frac{(\alpha^2+1)PR}{\alpha^2P+R} \] 其中,将PPV简记为P,TPR简记为R
当 \(\alpha=1\) 时,即\(F_1\)值,是召回率和精确率两者的均衡值,当 \(\alpha=2\) 时,即\(F_2\)值,结果侧重于精确率;当 \(\alpha=0.5\),即 \(F_{0.5}\)值,结果偏向于召回率
一般常用调和均值\(F_1\)反映算法的整体性能,即 \[ F_1 = \frac{2PR}{P+R} \]
而更一般的,\(F_1\)值会配合精确率和召回率一起使用,以更加综合地反映算法性能
1.3.2. P-R曲线
以召回率为横坐标,精确率为纵坐标,计算不同分类阈值下的PR值,并用一条线连接起来,便得到了一条P-R曲线。如下所示
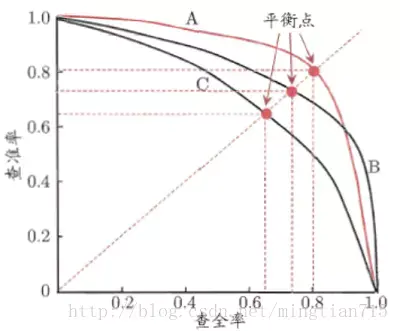
曲线下的面积越大,或者平衡点的值越大,算法性能越好。如果一个学习器的P-R曲线被另一个学习器的P-R曲线完全包住,则可断言后者的性能优于前者,例如上面的分类器B优于C,但是A和B的性能无法直接判断
1.3.3. ROC
ROC(Receiver Operating Characteristic Curve),受试者工作特征曲线,一种来源于二战时雷达兵对雷达的信号判断的评估指标。
其综合了召回率和脱落率(真实负样本中预测错误的概率),表达式为 \[ ROC=\frac{TPR}{FPR} \]
与PR曲线类似,以脱落率为横坐标,召回率为纵坐标,计算不同分类阈值下的ROC点,连接各点便可以得出ROC曲线,如下所示
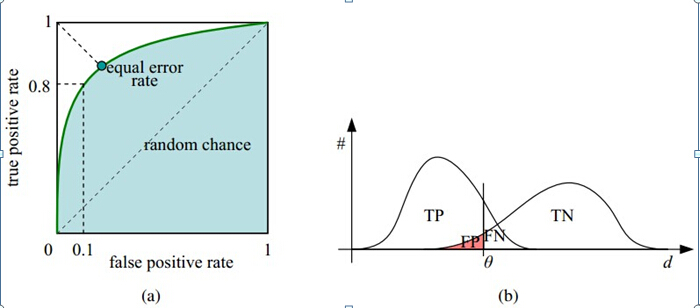
一般上,为了作图的完整性,还会额外增加一个零点,即输入4个阈值,会返回5个roc值,其中多出来的为原点,该点对应的阈值为score_max+1(sklearn中的做法)
TPR和FPR是两个相对量,当TPR越高时意味着正样本尽可能多地预测成正样本,当FPR越低时意味着负样本尽可能多地预测成负样本,即当ROC曲线越靠拢\((0,1)\)点,越偏离45度对角线时,算法的分类性能越好。对角线上的值表示模型没有任何排序性,即正负样本在每个分数区间上均匀分布的。当ROC曲线越靠拢\((1,0)\)点时,说明模型的预测结果是逆序的
相比于PR曲线,ROC曲线有一个巨大的优势就是,当正负样本的分布发生变化时,其形状能够基本保持不变,而P-R曲线的形状一般会发生剧烈的变化,因此该评估指标能降低不同测试集带来的干扰,更加客观的衡量模型本身的性能。
1.3.4. AUC
AUC(Area Under the Curve),ROC曲线下的面积。
其物理意义为:任取一对(正、负)样本,正样本的score大于负样本的score的概率,反映的是模型的总体性能。
其计算方法有3种:
对ROC曲线做积分,更加具体的,是求取每两个点间的梯形面积之和,但这种计算方法比较依赖精度和阈值,计算也很繁琐,一般不使用。
根据AUC的物理意义,计算所有正样本score大于负样本的score的期望,更加具体地,设正样本数为 \(M\),负样本数为 \(N\),计算公式为 \[ \frac{\sum_j^N\sum_i^{M} \left[I\left (P(x_i)>P(x_j) \right) + 0.5I\left(P(x_i)=P(x_j)\right) \right]}{NM} \] 计算复杂度为 \(O(NM)\)
与第二种方法相似,也是计算正样本score大于负样本的概率期望。首先把所有样本按照score排序,依次用\(r\)表示他们的次序(如果score值一样,那么r取均值,例如,\(r=3\)和\(r=4\)的score值一样,则两者的\(r=3.5\)),因为当前排名为 \(r\) 的样本比所有排名比其低的样本的score都要高,假设所有比排名为 \(r\) 的正样本排名要低的样本全是负样本,那么一共有 \(\sum_i^{M} r_i\) 个正样本比负样本score高的样本,如果除去一开始的假设,则还有去掉多计算的 \(M(M+1)/2\) 个正样本。最终计算公式为
\[ \frac{\sum_i^{M} r_i - M(M+1)/2}{NM} \] 计算复杂度为 \(O(N+M)\)
AUC取值的意义:
AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样,模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
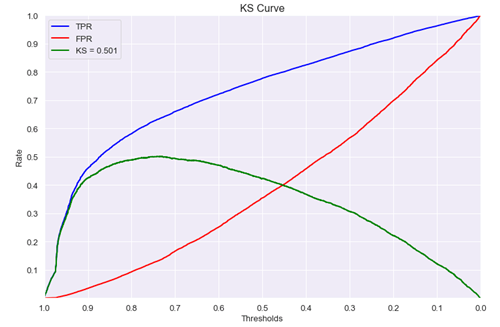
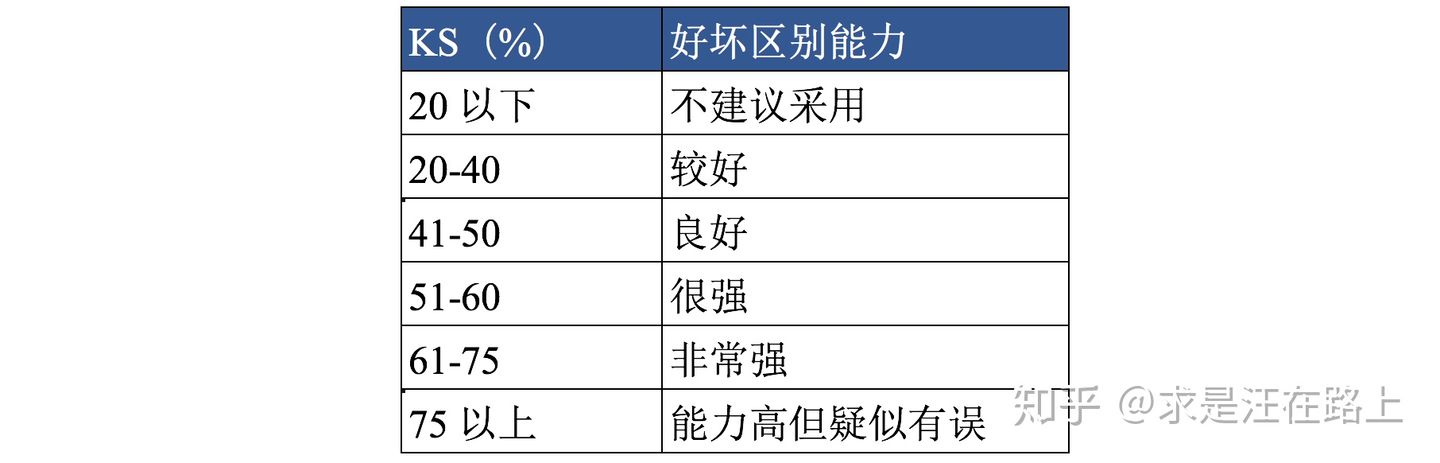
1.3.5. KS
KS与ROC的计算差不多,其定义为 \[ KS = |TPR-FPR| \] 其KS曲线趋势为
在ROC曲线中,每一点切线的截距就是其对应的KS值
一些参考建议
2. 多分类
二分类的一二三级指标都可以扩展为多分类情况。
例如,对二分类的的混淆矩阵中的类别进行扩展便得到多分类的混淆矩阵,其热力图下图所示
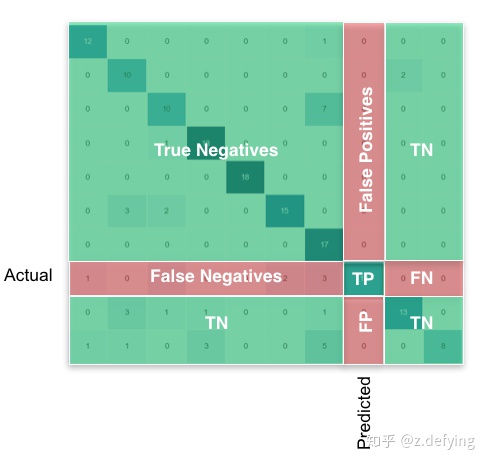
更加具体地,对于各级指标的计算,多分类没有对整个模型的度量指标(这里除了准确率可以对系统进行整体的评估,但得到的结果会偏小),都是单独地对各个分类标签(即以当前类别作为正样本,其他作为负样本,亦即OVR思想)的预测效果进行评估
3. references
【评分卡】评分卡入门与创建原则--分箱、WOE、IV、分值分配_scxyz的博客-CSDN博客_评分卡
Easy, isn't it?