1. 输入输出

Input:

观测序列 \[ O=(o_1,...,o_T) \] Output:

状态序列 \[ I=(i_1,...i_T) \]

2. 模型推导

MEMM可以认为是从HMM发展至CRF的中间产物，具有承上启下的作用。其算法推导可以从这两者入手。

2.1. 回顾HMM

首先来看HMM。HMM是生成式模型，学习的是联合概率，并具有两个假设：齐次马尔科夫性假设和观测独立性假设，具体用公式表示为 \[ P(I,O) = P\left(i_{t} \mid i_{t-1}\right) P\left(o_{t} \mid i_{t}\right) \] 但是HMM的独立性假设会带来一个问题：对于某个观测值，HMM认为其只由一个状态值决定，但对于多个状态值决定一个观测值的情况，HMM就无能为力了。

2.2. 改进HMM

于是MEMM取消了HMM的独立性假设，转而通过学习联合概率 $P(I\mid O)$ 建模，其对应模型也变为判别式的，这个模型和它的名字一样，本质上就是融入最大熵的分类思想和马尔科夫性，更加具体的用公式表示为 \[ P_{\bar{\mathrm{w}}}\left(i_{t} \mid i_{t-1}, o_{t}\right)=\frac{1}{Z_{\bar{\mathbf{w}}}\left(i_{t-1}, o_{t}\right)} \exp \left(\sum_{k} w_{k} f_{k}\left(i_{t}, i_{t-1}, o_{t}\right)\right) \] 其中 \[ Z_{\bar{\mathbf{w}}}\left(i_{t-1}, o_{t}\right)=\sum_{i_{t}} \exp \left(\sum_k w_{k} f_{k}\left(i_{t}, i_{t-1}, o_{t}\right)\right) \] HMM和MEMM更加形象的区别可以参照下图

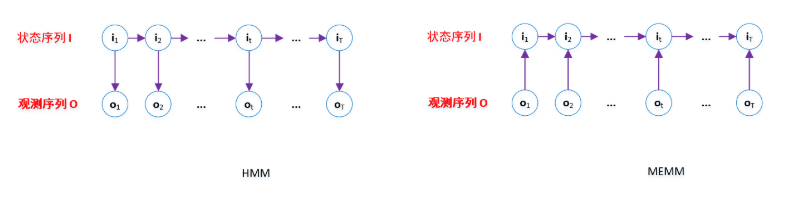
但是MEMM仍然存在一些问题：由于MEMM计算联合概率时仅考虑局部归一化，具体来说，在训练的时候，由于存在先验知识的原因，$i_t$ 和 $o_t$ 的对应关系是明确的，所以只考虑了 $ i_t$ 对 $i_{t+1}$ 的影响，但并没有考虑 $o_t$ 对 $i_{t+1}$ 的影响并没有考虑，这导致在测试的时候，我们并不能以一个很高的置信度由 $o_t$ 得出 $i_t$，所以上一时刻的不准确的预测就会累计到下一步的计算中，从而导致整体的预测错误，这也就是所谓的标注偏置问题。

特别的，苏神在这篇文章中提出可以使用一个双向的MEMM来减轻标注偏置带来的影响。

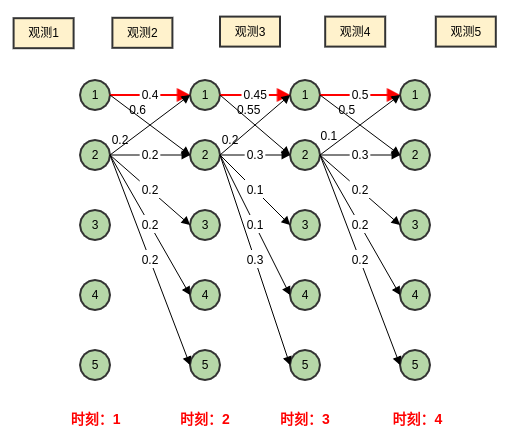
一个标注偏置的例子如下：

可以看出上面例子的最优路径是 1->1->1->1，这是不合理的。

2.3. 改进MEMM

为了解决上面的问题，继续对MEMM进行改进，从局部归一化扩展至全局归一化，便得到了CRF模型。具体用公式表示为 \[ P(I \mid O)=\frac{1}{Z(O)} \exp \left(\sum_{t, k} w_{k} f_{k}\left(i_{t-1}, i_{t}, o_{t}\right)\right) \]