无向图相关代码传送门
有向图相关代码传送门
1. 定义
图 \(G\) 由顶点集 \(V\) 和边集 \(E\) 组成,记为 \(G = (V, E)\)。(集合是图论中一个很重要的概念,后面也会多次用到集合这一概念)
图分为有向图和无向图。
2. 基本术语
子图
假设有两个图,\(G=(V,E)\) 和 \(G' = (V',E')\),如果,\(V' \subseteq V\) 且 \(E' \subseteq E\),则称 \(G'\) 为 \(G\) 的子图
无向完全图
具有 \(n(n-1)/2\) 条边的无向图
有向完全图
具有 \(n(n-1)\) 条边的有向图
网
每条边带有权值的图
邻接点
对于无向图,边 \((v, v') \in V\) ,称 \(v\) 和 \(v'\) 互为连接点
度
顶点 \(v\) 相关联的边的数目,记为 \(TD(v)\)。
特别地,对于有向图,又分为出度和入度。出度为以 \(v\) 为尾的边的数目,入度是以 \(v\) 为头的边的数目(可以粗略理解为,对于边 \((u, v) \in V\),\(v\) 是 \(u\) 的出度, \(u\) 是 \(v\) 的入度,当然度是数量词,对于带权值的网,度定义为以 \(v\) 为头的边的取值之和)
路径
顶点 \(v\) 到顶点 \(v'\) 的顶点序列 \((v, ...,v_i,...,v')\),其中经过的边的权值之和为路径长度
连通
对于无向图 \(G\),如果任意 \(v\) 到 \(v'\) 存在路径,则称 \(v\) 和 \(v'\) 是连通的,\(G\) 是一个连通图,\(G\) 中的极大连通子图为连通分量
强连通图
对于有向图 \(G\),如果所有 \(v\) 到 \(v'\) 都存在路径,则称 \(G\) 为强连通图。强连通图只有一个强连通分量
生成树
对于无向图 \(G\),存在一个极小连通子图,如果其包含图的所有 \(n\) 个顶点,有且仅有 \(n-1\) 条边,则称该连通子图为 \(G\) 的生成树。其中权值路径最小的为最小生成树
有向树
对于有向图 \(G\),存在一个 \(v\) 的入度为0,其他 \(v'\) 的入度均为1的子图,则称该子图为 \(G\) 的有向树(树型图),即有向图的生成树
3. 存储结构
3.1. 邻接矩阵
邻接矩阵(Adjacency Matrix)是一个n阶的矩阵,矩阵的值对应每条边的权值(没有权值默认为1,不连通默认为0或 \(\infty\))
例如,下面是一个上述无向图例子的邻接矩阵形式
[[0, 6, 1, 5, 0, 0],
[6, 0, 5, 0, 3, 0],
[1, 5, 0, 5, 6, 4],
[5, 0, 5, 0, 0, 2],
[0, 3, 6, 0, 0, 6],
[0, 0, 4, 2, 6, 0]]优点
便于计算两个顶点之间是否有边
便于计算各个顶点的度
缺点
不便于增/删顶点
不便于统计所有边的数目
空间复杂度高,不适用于稀疏图(稀疏图的特点:对于点集足够大的图,其点集的空间复杂度和边集的空间复杂度相近)
3.2. 邻接表
邻接表(Adjacency Table)是图的链式存储结构,虽然说是需要链式存储,但实际发现,需要应用到顺序排放的场景很少,所以这里我并没有按链式存储。
例如,下面是上面无向图的邻接表形式
{'B': {'E': 3, 'C': 5, 'A': 6},
'E': {'B': 3, 'C': 6, 'F': 6},
'A': {'D': 5, 'C': 1, 'B': 6},
'C': {'A': 1, 'B': 5, 'D': 5, 'F': 4, 'E': 6},
'D': {'F': 2, 'C': 5, 'A': 5},
'F': {'D': 2, 'E': 6, 'C': 4}}其优缺点临接矩阵的优缺点相反。
4. 可视化
4.1. 集合形式
以 \((v, v', weight)\) 的形式,给出给出图的边集
例如,下面是上述无向图的边集表示形式
[('E', 'C', 6), ('D', 'A', 5), ('F', 'D', 2), ('A', 'B', 6), ('A', 'C', 1), ('F', 'E', 6), ('C', 'B', 5), ('C', 'D', 5), ('C', 'F', 4), ('B', 'E', 3)]4.2. 文本形式
无向图以 v -- v' [weight] 形式或有向图以 u -> v [weight] 形式,给出图的边集
例如,下面是上述无向图的文本表示形式
D -- F [label="2"]
D -- C [label="5"]
D -- A [label="5"]
A -- B [label="6"]
F -- E [label="6"]
C -- E [label="6"]
A -- C [label="1"]
B -- E [label="3"]
C -- B [label="5"]
F -- C [label="4"]4.3. 图像形式
暂时还没很好的idea去怎样实现,难点在于如何安排每个点的布局,目前看到的解决方案有寻找子图,然后再想办法去安排这些子图的位置,后面有时间再去填这个坑。
现在有两种现成的替代方案:
- 使用python库networkx(并不是每次画出来的图都分布均匀,需要多试几次,而且这个工具绘制带权值的图并不好看,主要是绘制的文字不好看,也有使用权值作为边的宽度代替文字的解决方案,但感觉效果一般,所以索性就不绘制权值了)
- 使用graphviz(之前有介绍过这个工具,这里就不再介绍了。个人感觉这种方法做出来的图比networkx好看一点)
例如,下面是上述无向图的绘制效果
| nextworkx | graphviz |
|---|---|
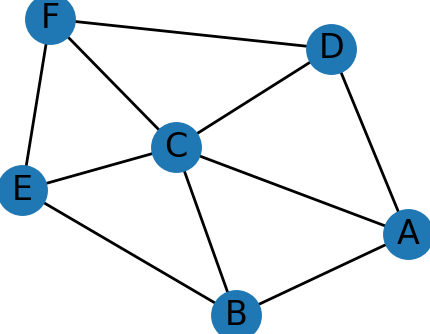 |
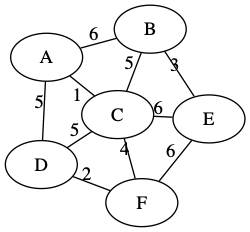 |
5. 遍历
这里以遍历输出生成树为例。
对于任意的连通的无向图,遍历的结果只有一棵生成树。
但对于任意的连通的有向图,遍历的结果可能是一个森林,所以需要多次遍历。如果要使森林中的树的数量尽可能少,则每次必须从入度最小的顶点开始遍历。
下面遍历算法的时间复杂度是一致的,使用邻接矩阵存储时,时间复杂度为 \(O(v^2)\);使用邻接表存储是,时间复杂为 \(O(v+e)\)
以下面的有向图的遍历为例。
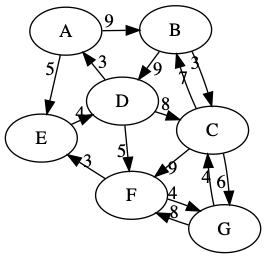
5.1. 深度优先(DFS)
- 创建一个用于记录每个顶点的状态数值,初始化所有都为假,用于表示每个顶点未被访问。
- 搜索图中入度最小的顶点,作为当前顶点。
- 把当前顶点设置为已访问,搜索当前顶点可以到达的且未被访问的顶点,把该顶点作为当前顶点。重复该步骤,直到当前顶点没有可以到达的且未被访问的顶点,递归返回。
- 重复步骤3,直到递归返回到其实顶点。
- 重复步骤2~4,直到所有的顶点都被访问。
上面有向图例子的遍历结果如下:
[('A', 'E', 5.0), ('E', 'D', 4.0), ('D', 'C', 8.0), ('C', 'G', 6.0), ('G', 'F', 8.0), ('C', 'B', 3.0)]5.2. 广度优先(BFS)
- 创建一个队列、一个用于记录每个顶点的状态数值,初始化所有都为假,用于表示每个顶点已被入队。
- 搜索图中入度最小的顶点,并把当前顶点入队,并设置为已入队。
- 把队头顶点出队,作为当前顶点,把当前顶点所有的可以到达的且未被访问的顶点入队,并全都设置为已入队,重复该步骤,直到队为空。
- 重复步骤2~3,直到所有的顶点都已经被入队。
上面有向图例子的遍历结果如下:
[('A', 'E', 5.0), ('A', 'B', 9.0), ('E', 'D', 4.0), ('B', 'C', 7.0), ('D', 'F', 5.0), ('C', 'G', 6.0)]5.3. 最小生成树
带权值的无向图的一种特殊的遍历——寻找图中路径长度最小的连通子图。
5.3.1. prim算法
算法流程如下:
- 初始化两个点集 \(u\) 和 \(v\),以及一个边集 \(g\) ,随机取一个顶点,将其加入 \(u\),图中的其他顶点加入 \(v\)。
- 从 \(v\) 中选取一个到 \(u\) 路径最小的点,将其从 \(v\) 中弹出并加入到 \(u\) 中,并把选到的边加入 \(g\) 中
- 重复步骤2,直到 \(v\) 为一个空集,边集 \(g\) 构成一棵最小生成树。
该算法的本质是归并点,时间复杂度为 \(O(v^2)\)
prim算法求解例子如下:
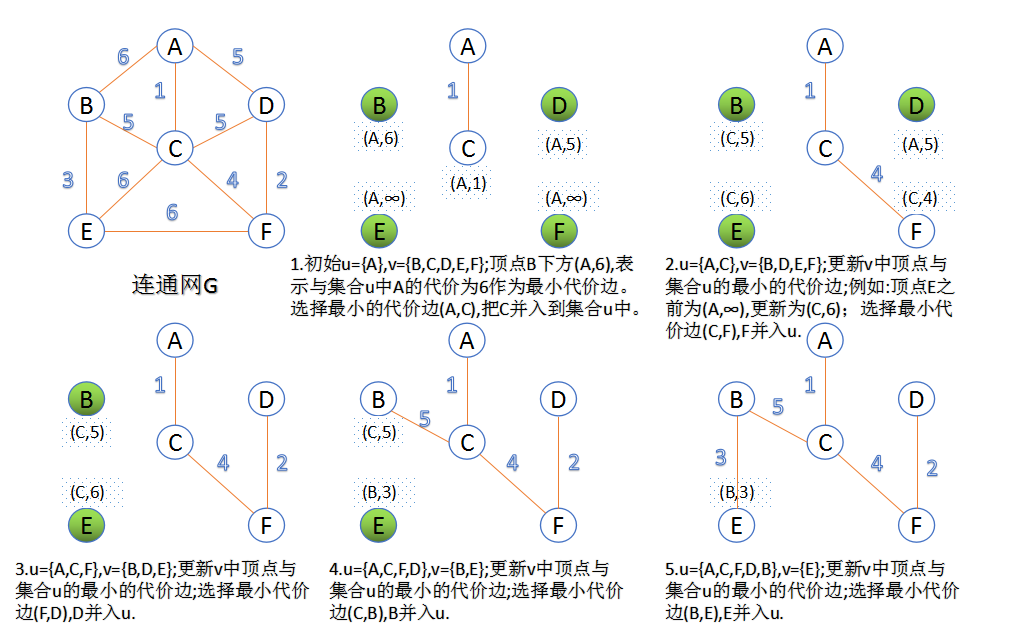
5.3.2. kruskal算法
算法流程如下:
- 把所有的边按权值升序排序,每一条边构成一张图。然后,从小到大遍历这个图集。
- 如果遍历到的边的两个顶点不在同一个连通图中,则合并这两个图。否则,抛弃这一条边。
- 重复步骤2,直到所有的顶点都在同一张连通图中。这张连通图就是一棵最小生成树。
该算法的本质是归并边,时间复杂度为 \(O(e \log e)\)
kruskal算法求解例子如下:
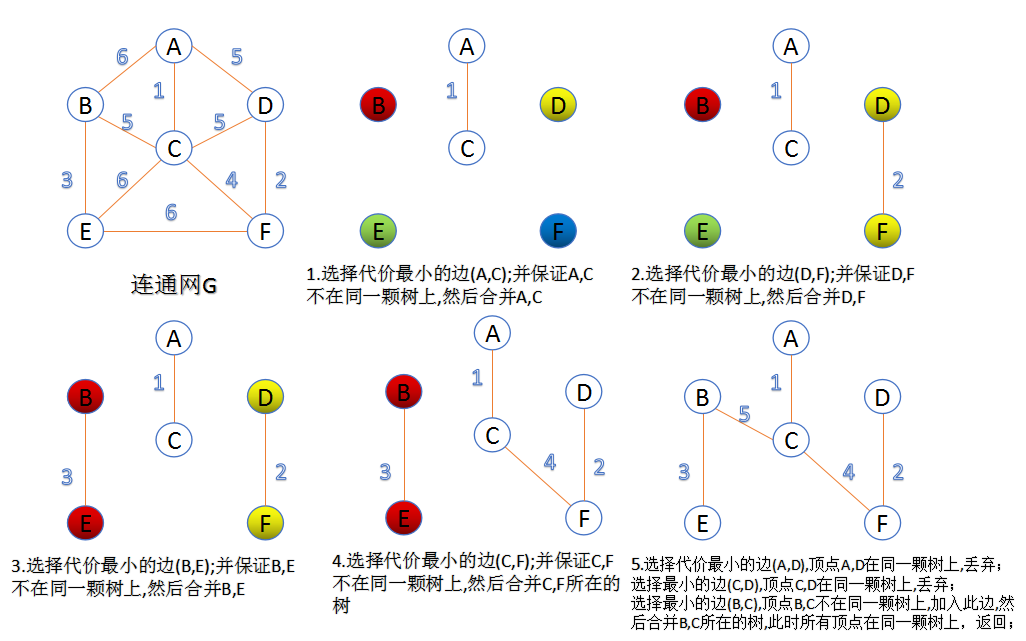
5.4. 最小树型图
最小树形图即带权值的有向图的最小生成树。
上面无向图最小生成树的两个算法本质上都是贪心的,由于有向图存在单向边,当存在有向环时,会出现多条单向路径的情况,故从随机挑选的点出发,每次的贪心选择不一定是安全,即不一定都能找到最优解,所以无向图的生成树算法并不适用于所有的有向图。
现在应用较广泛的是1965年提出来的朱刘算法
网上大多是给定根节点的求解情况,不具有鲁棒性。对于不定根的情况,其实只要设立一个超级源点,作为给定的虚拟根,该虚拟根到图中的所有点的权值一样并趋向于无穷大(一般设为图的所有边的权值之和+1来表示无穷大),表示该虚拟根不会影响最终结果(只要对最后求出来的去掉该虚拟根即可)
下面给出不定根的求解步骤:
- 创建一个超级源点作为给定的虚根,该点到图中所有点的权值为图的所有边的权值之和+1。
- 除根节点外,每个顶点选择一条最小的指向自身的边,组成一个最短边集 \(V\) 。
- 如果 \(V\) 中,存在除根节点外的孤立点(即入度为0)的点,则没有最小树型图,算法结束。
- 如果 \(V\) 中,存在有向环,则转到步骤4,如果不存在,则转到步骤5.
- 把有向环收缩成一个点,对所有指向这个收缩点的边(入度)的权值进行更新(更新规则为:假设收缩后的点为 \(u\),收缩前存在边集 \((v_0, v_1)\),\(v_0\) 为不收缩的点,\(v_1\) 为待收缩的点,\((v_0, v_1)\)的权值为 \(w_0\),\(v_1\) 前序顶点的权值为 \(w_1\),则 \((v_0, u)\) 的权值为 \((w_0-w_1)\));如果存在多条指向这个收缩点的边时,取最小边。然后重复步骤2~4
- 展开 \(V\) 中所有的收缩点,深度遍历边集得到的树,即为最小树型图。
可以看出,该算法的思想有一点kruskal算法的味道,只不过做了额外的优化,通过不断把有向环看作一个点,把多条路径简化为单一路径,确保了算法可以找到的是连通的边集。
下面是给点 \(V_1\) 作为根节点的求解例子
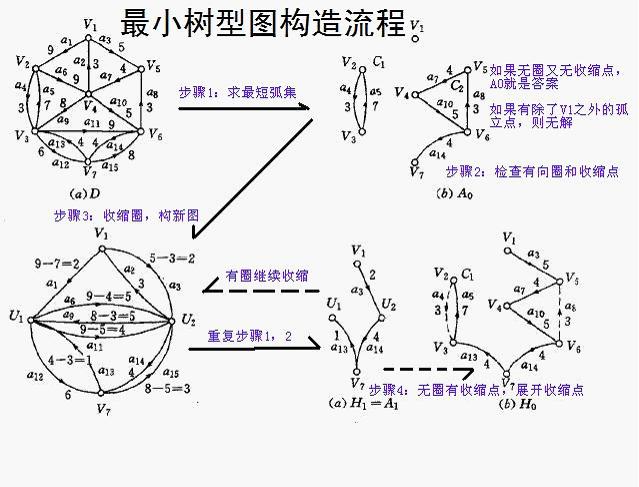
上边指定的是 \(V_1\) 作为根节点,路径为 V1 -> V5 -> V4 -> V6 -> V7 -> V3 -> V2 ,路径长度为29
如果是不给定根节点的最小生成树应该是以 \(V_6\) 为根节点,路径为 V2 <- V3 <- V7 <- V6 -> V5 -> V4 -> V1,路径长度为25
6. 最短路径
图的最短路径即两点间的路径长度之和最短的路径,最常应用于导航寻路、路由跳转等。
下面的算法无向图和有向图都适用。
下面以某两点间的最短路径为例(当然这个可以扩展为任意一点到其他各点的最短路径)
6.1. dijkstra算法
算法流程如下:
- 创建一个用于保存到当前顶点的路径长度数组 \(w\) ,并初始化为无穷大(开始顶点为0);一个用于保存当前顶点的前序顶点索引的数组 \(p\) ,初始化为-1;以及一个用于保存已遍历过的顶点的集合 \(u\) ,并把开始顶点作为当前顶点,加入该集合中。
- 更新 \(w\) 和 \(p\)。遍历当前顶点到其他未被遍历过的顶点的权值。例如,如果当前顶点的路径长度 \(w_1\),当前顶点到顶点 \(v\) 的权值为 \(w_2\),顶点 \(v\) 的路径长度为 \(w_3\),如果 \(w_1+w_2<w_3\) ,则更新 \(w_3 = w_1+w_2\),并把 \(v\) 的前序顶点设置为当前顶点。
- 从\(w\)中选择值最小的顶点,如果该顶点在 \(u\) 中,则把该顶点的路径长度从 \(w\) 中排除,重复该步骤(这里可以使用最小堆来减少时间复杂度),直到该顶点不在 \(u\) 中或遍历完所有路径长度不为无穷大的顶点。如果可以找到顶点,则把该顶点作为当前顶点,并将其加入 \(u\) 中,否则说明开始点和终止点是不连通的,这两点间不存在路径,算法结束。
- 重复步骤2~3,直到当前顶点为终止顶点,按 \(p\) 中从终止顶点开始的前向溯源,得到最短路径。
该算法的思想是按路径长度递增地产生最短路径,每一条最短路径都是基于已求的路径产生的,是典型的动态规划思想,时间复杂度为 \(O(v^2)\)
6.2. floyed算法
算法流程如下:
- 创建一个空的边集,将开始顶点和终止顶点作为初始值,输入到步骤2中。
- 对于输入的 \((v_i, v_j)\),寻找一个顶点 \(v_0\),使得 \((v_i, v_0, v_j)\) 的路径长度小于 \((v_i, v_j)\) 的路径长度,如果能找到,则分成 \((v_i, v_0)\) 和 \((v_0, v_j)\) 两部分,分别作为输入,重复该步骤;如果不能找到,则说明输入的边为两点的最短路径,将输入的边加入到边集中,递归返回。
- 最终的到边集构成了两点间的最短路径。
如果是要求任意顶点到所有任意顶点的最短路径,则可以不使用递归,直接创建两个图的邻接矩阵大小的辅助矩阵,一个用于记录两点间的路径长度,一个用于记录两点最短路径的中间顶点,然后用一个循环按照算法的思想更新两个矩阵的每一个值,最后通过终止顶点前向溯源寻找开始顶点,即可找到最短路径。时间复杂度为 \(O(v^3)\)
7. 拓扑排序
只有有向无环图(Directed Acycline Graph, DAG)才会有拓扑排序,相反地,我们也可以利用是否由拓扑排序来判断是否是一个有向无环图。
下面是一个DAG图
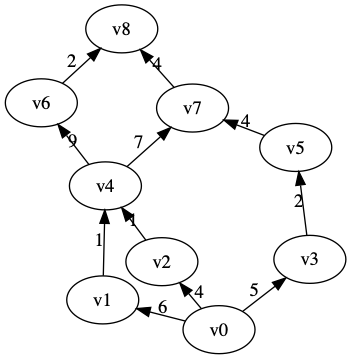
排序过程:
- 创建一个队列,一个空的点集序列;求出图中各顶点的入度。
- 把入度为0的顶点入队,并把已经入队的顶点的入度设为-1
- 队头元素出队,加入点集序列,并设为当前顶点。当前顶点的邻接点的入度-1
- 重复步骤2~3,直到队列为空,得到的点集序列为所求拓扑排序。
时间复杂度为 \(O(v+e)\)
上面DAG图的拓扑排序为
['v0', 'v1', 'v2', 'v3', 'v4', 'v5', 'v6', 'v7', 'v8']8. 关键路径
对于DAG图,我们分成两类:
- 用顶点表示活动、边表示活动的优先关系的,称为AOV-网(Activity On Vertex Network)
- 用顶点表示事件、边表示活动,权值表示活动持续时间,称为AOE-网(Activity On Edge)
关键路径是求解AOE-网中的最长路径
求解过程:
- 求出AOE的拓扑排序。
- 从前往后求拓扑排序中每个顶点的最早发生时间。创建一个 \(ve\) 数组,并初始化为0,用于保存拓扑排序中每个顶点的最早发生时间。遍历更新过程:设当前顶点为 \(v_0\),拓扑排序中的下边为 \(i_0\);遍历其邻接顶点,设 \(v_1\) 为其中的一个邻接顶点,拓扑排序中的下标为 \(i_1\),两顶点间的权值为 \(v\),则 \(ve_{i_1} = max(ve_{i_1}, ve_{i_0} + v)\)
- 从后往前求拓扑排序中每个顶点的最晚发生时间。创建一个 \(vl\) 数组,并初始化为\(ve_{n-1}\),用于保存拓扑排序中每个顶点的最晚发生时间。遍历更新过程:设当前顶点为 \(v_0\),拓扑排序中的下边为 \(i_0\);遍历其邻接顶点,设 \(v_1\) 为其中的一个邻接顶点,拓扑排序中的下标为 \(i_1\),两顶点间的权值为 \(v\),则 \(vl_{i_0} = min(vl_{i_0}, vl_{i_1} - v)\)
- 从前往后判断关键活动。判断过程:设当前顶点为 \(v_0\),拓扑排序中的下边为 \(i_0\);遍历其邻接顶点,设 \(v_1\) 为其中的一个邻接顶点,拓扑排序中的下标为 \(i_1\),两顶点间的权值为 \(v\),如果 \(ve_{i_0} = vl_{i_1} - v\),则 \((v_0, v_1)\) 为关键路径。
上述DAG的关键路径为
[('v0', 'v1', 6), ('v1', 'v4', 1), ('v4', 'v6', 9), ('v4', 'v7', 7), ('v6', 'v8', 2), ('v7', 'v8', 4)]可以看出,关键路径可以存在多条。
That's all~ It's a sunny day again~